位运算 | 基本算法

参考《算法竞赛进阶指南》、AcWing题库

位运算

bit 是度量信息的单位, 包含 0 和 1 两种状态。计算机的各种运算最后无不归结为 一个个 bit 的变化。熟练掌握并利用位运算, 能够帮助我们理解程序运行中的种种表现, 提高程序运行的时空效率, 降低编程复杂度。

在 $\mathrm{C}++$ 中, 8 位二进制数对应 char 类型, 范围 为 $-128 \sim 127$, 其中 $0 \times F F$ 代表一1, $0 \times 7 F$ 代表最大值 127 。

在阅读本节之前, 读者应该对以下算术位运算有一个初步的认识:

与	或	非	异或
$and,\&$	$or,	$	$not,\sim$

它们不局限于逻辑运算, 均可作用于二进制整数。为了避免混淆, 统一用单词 xor 表示异或运算, 而用符号 “^” 表示乘方运算 (虽然该符号在 C++中表示异或)。

另外, 在 $m$ 位二进制数中, 为方便起见, 通常称最低位为第 0 位, 从右到左依此类推, 最高位为第 $m-1$ 位。默认使用这种表示方法来指明二进制数以及整数在二进制表示下的位数。

下面我们以 32 位二进制数, 即 $\mathrm{C}++$ 的 int 与 unsigned int 类型为例详细介绍计算机中的整数存储与运算。

补码

32 位无符号整数 unsigned int:

直接把这 32 位编码 $C$ 看作 32 位二进制数 $N$ 。

32 位有符号整数 int:

以最高位为符号位, 0 表示非负数, 1 表示负数。

对于最高位为 0 的每种编码 $C$, 直接看作 32 位二进制数 $S$ 。

同时, 定义该编码按位取反后得到的编码 $\sim C$ 表示的数值为 $-1-S$ 。

32位补码表示	unsigned int	int
$000000\cdots000000$	0	0
$011111\cdots111111$	2 147 483 647	2 147 483 647
$100000\cdots000000$	2 147 483 648	-2 147 483 648
$111111\cdots111111$	4 294 967 295	-1

可以发现在补码下每个数值都有唯一的表示方式, 并且任意两个数值做加减法运算, 都等价于在 32 位补码下做最高位不进位的二进制加减法运算。发生算术溢出时, 32 位无符号整数相当于自动对 $2^{32}$ 取模。这也解释了 “有符号整数” 算术上溢时出现负数的现象。

补码也被称为 “二补数”。还有一种编码称为反码, 也叫 “一补数” , 直接把 $C$ 的每一位取反表示负 $C$ 。补码与反码在负数表示中, 绝对值相差 1。例如, 在上表中, 第 1、4行是一对反码, 第 $2 、 3$ 行是一对反码。作为整数编码、存储和运算的方式, 补码与反码相比有许多优势。除了上面提到的 “自然溢出取模” 之外, 补码重点解决了 0 的编码唯一性问题, 能比反码多表示一个数, 同时减少特殊判断, 在电路设计中极其简单、高效。

形式	加数	加数	和
32位补码	$111\cdots111$	$000\cdots001$	(1)$000\cdots000$
int	-1	1	0
unsigned int	4 294 967 295	1	0(mod $2^{32}$)
32位补码	$011\cdots111$	$000\cdots001$	0
int	2 147 483 647	1	-2 147 483 648
unsigned int	2 147 483 647	1	2 147 483 648

因为用二进制表示一个 int 需要写出 32 位, 比较繁琐, 而用十进制表示, 又不容易明显地体现出补码的每一位, 所以在程序设计中, 常用十六进制来表示一个常数, 这样只需要书写 8 个字符, 每个字符 $(0 \sim 9, A \sim F)$ 代表补码下的 4 个二进制位。 $C++$ 的十六进制常数以 “ $0 \mathrm{x}$ ” 开头, “ $0 \mathrm{x}$ ” 本身只是声明了进制, “ $0 \mathrm{x}$ ” 后面的部分对应具体的十六进制数值。例如:

32位补码表示	int（十进制）	int（十六进制）
$000000\cdots000000$	0	0x0
$011111\cdots111111$	2 147 483 647	0x7F FF FF FF
0011 1111 重复4次	1 061 109 567	0x3F 3F 3F 3F
$111111\cdots111111$	-1	-1

上表中的 0x3F 3F 3F 3F 是一个很有用的数值, 它是满足以下两个条件的最大整数。

1. 整数的两倍不超过 0x7F FF FF FF , 即 int 能表示的最大正整数。
2. 整数的每 8 位 (每个字节) 都是相同的。

我们在程序设计中经常需要使用 memset ( a, val, sizeof(a)) 初始化一个 int 数组 $a$ , 该语句把数值 val (0x00 ~ 0xFF) 填充到数组 $a$ 的每个字节上, 而 1 个 int 占用 4 个字节, 所以用 memset 只能赋值出 “每 8 位都相同” 的 int。

综上所述, 0x7F FF FF FF 是用 memset 语句能初始化出的最大数值。不过, 当需要把一个数组中的数值初始化成正无穷时, 为了避免加法算术上温或者繁琐的判断, 我们经常用 memset (a, 0x3f, sizeof (a)) 给数组赋 0x3F 3F 3F 3F 的值来代替。

$2^{30}=1 073 741 824$

移位运算

左移

在二进制表示下把数字同时向左移动, 低位以 0 填充, 高位越界后舍弃。

$$1 \ll n=2^{n}, \quad n \ll 1=2 n$$

算术右移

在二进制补码表示下把数字同时向右移动, 高位以符号位填充, 低位越界后舍弃。

$$n \gg 1=\left\lfloor\frac{n}{2.0}\right\rfloor$$

算术右移等于除以 2 向下取整, $(-3) \gg 1=-2,3 \gg 1=1$ 。

值得一提的是, “整数/2” 在 C++ 中实现为 “除以 2 向零取整”, $(-3) / 2=-1,\;3 / 2=1$ 。

逻辑右移

在二进制补码表示下把数字同时向右移动, 高位以 0 填充, 低位越界后舍弃。

C++语法没有规定右移的实现方式, 使用算术右移还是逻辑右移由编译器决定。一般的编译器 (较新版本的 GNU C++与 Visual StudioC++ 均使用算术右移。除非特殊提示, 我们默认右移操作采用算术右移方式实现。

89. a^b

题目描述

求 $a$ 的 $b$ 次方对 $p$ 取模的值。

输入格式

三个整数 $a,b,p$ ,在同一行用空格隔开。

输出格式

输出一个整数，表示a^b mod p的值。

数据范围

$0 \le a,b \le 10^9$
$1 \le p \le 10^9$

输入样例：

3 2 7 

输出样例：

2 

算法分析

根据数学常识, 每一个正整数可以唯一表示为若干指数不重复的 2 的次幂的和。 也就是说, 如果 $b$ 在二进制表示下有 $k$ 位, 其中第 $i(0 \leq i<k)$ 位的数字是 $c_{i}$, 那 么:

$$b=c_{k-1} 2^{k-1}+c_{k-2} 2^{k-2}+\cdots+c_{0} 2^{0}$$

于是:

$$a^{b}=a^{c_{k-1} * 2^{k-1}} * a^{c_{k-2} * 2^{k-2}} * \cdots * a^{c_{0} * 2^{0}}$$

因为 $k=\left\lceil\log _{2}(b+1)\right\rceil$ (其中 $\lceil\;\rceil$ 表示上取整), 所以上式乘积项的数量不多于 $\left\lceil\log _{2}(b+1)\right\rceil$ 个。又因为:

$$a^{2^{i}}=\left(a^{2^{i-1}}\right)^{2}$$

所以我们很容易通过 $k$ 次递推求出每个乘积项, 当 $c_{i}=1$ 时, 把该乘积项累积到答案中。 $b \& 1$ 运算可以取出 $b$ 在二进制表示下的最低位, 而 $b \gg1$ 运算可以舍去最低位, 在递推的过程中将二者结合, 就可以遍历 $b$ 在二进制表示下的所有数位 $c_{i}$ 。整个算法的时间复杂度为 $O\left(\log _{2} b\right)$ 。

// 快速幂，求a^b mod p
int power(int a, int b, int p) {
	int ans = 1;
	for (; b; b >>= 1) {
		if (b & 1) ans = (long long)ans * a % p;
		a = (long long)a * a % p;
	}
	return ans;
}

在上面的代码片段中, 我们通过 “右移 $(>>)$ ” “与 ( $\&$ ) ” 运算的结合, 遍历了 $b$ 的二进制表示下的每一位。在循环到第 $i$ 次时 (从 0 开始计数), 变量 $a$ 中存储的是 $a^{2^{i}}$, 若 $b$ 该位为 1 , 则把此时的变量 $a$ 累积到答案 ans 中。

值得提醒的是, 在 C++ 语言中, 两个数值执行算术运算时, 以参与运算的最高数值类型为基准, 与保存结果的变量类型无关。换言之, 虽然两个 32 位整数的乘积可能超过 int 类型的表示范围，但 CPU 只会用 1 个 32 位寄存器保存结果，造成我们常说的越界现象。因此，我们必须把其中一个数强制转换成64位整数类型 long long 参与运算，从而得到正确的结果。最终对 p 取模以后，执行赋值操作时，该结果会被隐式转换成 int 存回 ans 中。从而得到正确的结果。

于是一个问题就出现了。因为 C++ 内置的最高整数类型是 64 位, 若运算 $a*b\bmod p$ 中的三个变量 $a, b, p$ 都在 $10^{18}$ 级别, 则不存在一个可供强制转换的 128 位整数类型，我们需要一些特殊的处理方法。

Solution

---

90. 64位整数乘法

题目描述

求 $a$ 乘 $b$ 对 $p$ 取模的值。

输入格式

第一行输入整数$a$，第二行输入整数$b$，第三行输入整数$p$。

输出格式

输出一个整数，表示a*b mod p的值。

数据范围

$1 \le a,b,p \le 10^{18}$

输入样例：

3
4
5 

输出样例：

2 

算法分析

方法一

类似于快速幂的思想, 把整数 $b$ 用二进制表示, 即 $b=c_{k-1} 2^{k-1}+c_{k-2} 2^{k-2}+$ $\cdots+c_{0} 2^{0}$, 那么 $a * b=c_{k-1} * a * 2^{k-1}+c_{k-2} * a * 2^{k-2}+\cdots+c_{0} * a * 2^{0}$ 。

因为 $a * 2^{i}=\left(a * 2^{i-1}\right) * 2$, 若已求出 $a * 2^{i-1} \bmod p$, 则计算 $\left(a * 2^{i-1}\right) *$ $2 \bmod p$ 时, 运算过程中每一步的结果都不超过 $2 * 10^{18}$, 仍然在 64 位整数 long long 的表示范围内, 所以很容易通过 $k$ 次递推求出每个乘积项。当 $c_{i}=1$ 时, 把该乘积 项累加到答案中即可。时间复杂度为 $\mathrm{O}\left(\log _{2} b\right)$ 。

// 64位整数乘法的O(log b)算法
long long mul(long long a, long long b, long long p) {
	long long ans = 0;
	for (; b; b >>= 1) {
		if (b & 1) ans = (ans + a) % p;
		a = a * 2 % p;
	}
	return ans;
}

方法二

利用 $a * b \bmod p=a * b-\lfloor a * b / p\rfloor * p$, 其中 $\lfloor\;\rfloor$ 表示下取整。

首先, 当 $a, b<p$ 时, $a * b / p$ 下取整以后一定也小于 $p$ 。我们可以用浮点数执行 $a * b / p$ 的运算, 而不用关心小数点之后的部分。浮点类型 long double 在十进制下的有效数字有 18 ~ 19 位, 足够胜任。当浮点数的精度不足以保存精确数值时, 它会像科学计数法一样舍弃低位, 正好符合我们的要求。

另外, 虽然 $a * b$ 和 $\lfloor a * b / p\rfloor * p$ 可能很大, 但是二者的差一定在 $0 \sim p-1$ 之间, 我们只关心它们较低的若干位即可。所以, 我们可以用 long long 来保存 $a * b$ 和 $\lfloor a * b / p\rfloor * p$ 各自的结果。整数运算溢出相当于舍弃高位, 也正好符合我们的要求。

64位整数乘法的long double算法

typedef unsigned long long ull;
ull mul(ull a, ull b, ull p) {
	a %= p, b %= p;  // 当a,b一定在0~p之间时，此行不必要
	ull c = (long double)a * b / p;
	ull x = a * b, y = c * p;
	long long ans = (long long)(x % p) - (long long)(y % p);
	if (ans < 0) ans += p;
	return ans;
}

Solution

---

二进制状态压缩

二进制状态压缩, 是指将一个长度为 $m$ 的 bool 数组用一个 $m$ 位二进制整数表示并存储的方法。利用下列位运算操作可以实现原 bool 数组中对应下标元素的存取。

$$\begin{array}{l|l} {\text { 操作 }} & {\text { 运算 }} \\ \hline \text { 取出整数 } n \text { 在二进制表示下的第 } k \text { 位 } & (n \gg k) \& 1 \\ \text { 取出整数 } n \text { 在二进制表示下的第 } 0 \sim k-1 \text { 位 }(\text { 后 } k \text { 位 }) & n \&((1 \ll k)-1) \\ \text { 把整数 } n \text { 在二进制表示下的第 } k \text { 位取反 } & n \text { xor }(1 \ll k) \\ \text { 对整数 } n \text { 在二进制表示下的第 } k \text { 位赋值 } 1 & n \mid(1 \ll k) \\ \text { 对整数 } n \text { 在二进制表示下的第 } k \text { 位赋值 } 0 & n \&(\sim(1 \ll k)) \end{array}$$

这种方法运算简便, 并且节省了程序运行的时间和空问。当 $m$ 不太大时, 可以直接使用一个整数类型存储。当 $m$ 较大时, 可以使用若干个整数类型 (int 数组), 也可以直接利用 C++ STL 为我们提供的 bitset 实现。

---

91. 最短Hamilton路径

题目描述

给定一张 $n$ 个点的带权无向图，点从 $0 \sim n-1$ 标号，求起点 $0$ 到终点 $n-1$ 的最短 Hamilton 路径。

Hamilton 路径的定义是从 $0$ 到 $n-1$ 不重不漏地经过每个点恰好一次。

输入格式

第一行输入整数 $n$。

接下来 $n$ 行每行 $n$ 个整数，其中第 $i$ 行第 $j$ 个整数表示点 $i$ 到 $j$ 的距离（记为 $a[i,j]$）。

对于任意的 $x,y,z$，数据保证 $a[x,x]=0，a[x,y]=a[y,x]$ 并且 $a[x,y]+a[y,z] \ge a[x,z]$。

输出格式

输出一个整数，表示最短 Hamilton 路径的长度。

数据范围

$1 \le n \le 20$
$0 \le a[i,j] \le 10^7$

输入样例：

5
0 2 4 5 1
2 0 6 5 3
4 6 0 8 3
5 5 8 0 5
1 3 3 5 0 

输出样例：

18 

算法分析

很容易想到本题的一种 “朴素” 做法, 就是枚举 $n$ 个点的全排列, 计算路径长度取最小值, 时问复杂度为 $O(n * n !)$, 使用下面的二进制状态压缩 DP 可以优化到 $O\left(n^{2} * 2^{n}\right)$ 。

在任意时刻如何表示哪些点已经被经过, 哪些点没有被经过? 可以使用一个 $n$ 位二进制数, 若其第 $i$ 位 $(0 \leq i<n)$ 为 1 , 则表示第 $i$ 个点已经被经过, 反之未被经过。在任意时刻还需要知道当前所处的位置, 因此我们可以使用 $F[i, j]\left(0 \leq i<2^{n}, 0 \leq\right.$ $j<n)$ 表示 “点被经过的状态” 对应的二进制数为 $i$, 且目前处于点 $j$ 时的最短路径。

在起点时, 有 $F[1,0]=0$, 即只经过了点 0 ( $i$ 只有第 0 位为 1 ), 目前处于起点 0 , 最短路长度为 0 。方便起思, 我们将 $F$ 数组其他的值设为无穷大。最终目标是 $F[(1 \ll n)-1, n-1]$, 即经过所有点 $(i$ 的所有位都是 1$)$, 处于终点 $n-1$ 的最短路。

在任意时刻, 有公式 $F[i, j]=\min \{F[i \text{ xor } (1 \ll j), k]+\operatorname{weight}(k, j)\}$, 其中 $0\leq k<n$ 并且 $((i \gg j) \& 1)=1$ , 即当前时刻 “被经过的点的状态” 对应的二进制数为 $i$ , 处于点 $j$ 。因为 $j$ 只能被恰好经过一次, 所以一定是刚刚经过的, 故在上一时刻 “被经过的点的状态” 对应的二进制数的第 $j$ 位应该赋值为 0 , 也就是 $i \text{ xor } (1 \ll j)$ 。另外, 上一时刻所处的位置可能是 $i \text { xor } (1 \ll j)$ 中任意一个是 1 的数位 $k$ , 从 $k$ 走到 $j$ 需经过 $\operatorname{weight}(k, j)$ 的路程, 可以考虑所有这样的 $k$ 取最小值。这就是该公式的由来。

// hamilton路径
int f[1 << 20][20];
int hamilton(int n, int weight[20][20]) {
	memset(f, 0x3f, sizeof(f));
	f[1][0] = 0;
	for (int i = 1; i < 1 << n; i++)
		for (int j = 0; j < n; j++)
			if (i >> j & 1)
				for (int k = 0; k < n; k++)
					if (i >> k & 1)
						f[i][j] = min(f[i][j], f[i ^ 1 << j][k] + weight[k][j]);
	return f[(1 << n) - 1][n - 1];
}

提醒: 一些运算符优先级从高到低的顺序如下页表所示。最需要注意的地方是: 大 小关系比较的符号优先于 “位与” “异或” “位或” 运算。在程序实现时, 如果不确定优 先级, 建议加括号保证运算顺序的正确性。

$$\begin{array}{c|c|c|c|c|c} \text { 加减 } & \text { 移位 } & \text { 比较大小 } & \text { 位与 } & \text { 异或 } & \text { 位或 } \\ \hline+,- & \ll, \gg & \geqslant,<,==, != & \& & \text { xor }\left(\mathrm{C}++^{\wedge}\right) & 1 \end{array}$$

Solution

---

998. 起床困难综合症

题目描述

$21$ 世纪，许多人得了一种奇怪的病：起床困难综合症，其临床表现为：起床难，起床后精神不佳。

作为一名青春阳光好少年，atm 一直坚持与起床困难综合症作斗争。

通过研究相关文献，他找到了该病的发病原因： 在深邃的太平洋海底中，出现了一条名为 drd 的巨龙，它掌握着睡眠之精髓，能随意延长大家的睡眠时间。

正是由于 drd 的活动，起床困难综合症愈演愈烈， 以惊人的速度在世界上传播。

为了彻底消灭这种病，atm 决定前往海底，消灭这条恶龙。

历经千辛万苦，atm 终于来到了 drd 所在的地方，准备与其展开艰苦卓绝的战斗。

drd 有着十分特殊的技能，他的防御战线能够使用一定的运算来改变他受到的伤害。

具体说来，drd 的防御战线由 $n$ 扇防御门组成。

每扇防御门包括一个运算 $op$ 和一个参数 $t$，其中运算一定是 $OR,XOR,AND$ 中的一种，参数则一定为非负整数。

如果还未通过防御门时攻击力为 $x$，则其通过这扇防御门后攻击力将变为 $x\ op\ t$。

最终 drd 受到的伤害为对方初始攻击力 $x$ 依次经过所有 $n$ 扇防御门后转变得到的攻击力。

由于 atm 水平有限，他的初始攻击力只能为 $0$ 到 $m$ 之间的一个整数（即他的初始攻击力只能在 $0, 1, … , m$ 中任选，但在通过防御门之后的攻击力不受 $m$ 的限制）。

为了节省体力，他希望通过选择合适的初始攻击力使得他的攻击能让 drd 受到最大的伤害，请你帮他计算一下，他的一次攻击最多能使 drd 受到多少伤害。

输入格式

第 $1$ 行包含 $2$ 个整数，依次为 $n, m$，表示 drd 有 $n$ 扇防御门，atm 的初始攻击力为 $0$ 到 $m$ 之间的整数。

接下来 $n$ 行，依次表示每一扇防御门。每行包括一个字符串 $op$ 和一个非负整数 $t$，两者由一个空格隔开，且 $op$ 在前，$t$ 在后，$op$ 表示该防御门所对应的操作，$t$ 表示对应的参数。

输出格式

输出一个整数，表示 atm 的一次攻击最多使 drd 受到多少伤害。

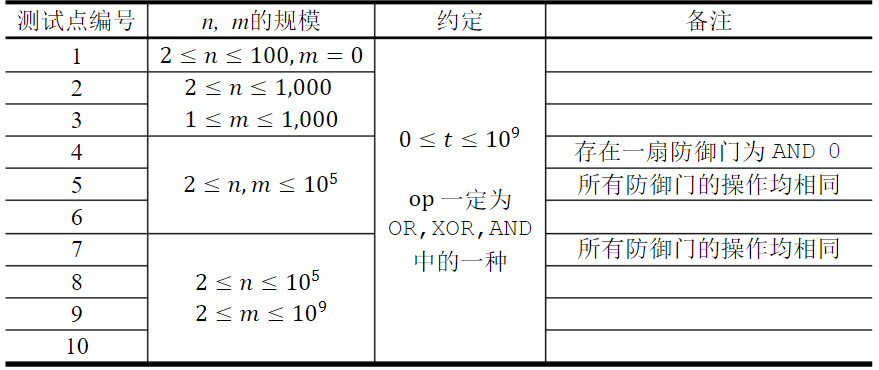
数据范围

输入样例：

3 10
AND 5
OR 6
XOR 7 

输出样例：

1 

样例解释

atm可以选择的初始攻击力为 $0,1, … ,10$。

假设初始攻击力为 $4$，最终攻击力经过了如下计算

4 AND 5 = 4

4 OR 6 = 6

6 XOR 7 = 1 

类似的，我们可以计算出初始攻击力为 $1,3,5,7,9$ 时最终攻击力为 $0$，初始攻击力为 $0,2,4,6,8,10$ 时最终攻击力为 $1$，因此 atm 的一次攻击最多使 drd 受到的伤害值为 $1$。

运算解释

在本题中，选手需要先将数字变换为二进制后再进行计算。如果操作的两个数二进制长度不同，则在前补 $0$ 至相同长度。

• OR 为按位或运算，处理两个长度相同的二进制数，两个相应的二进制位中只要有一个为 $1$，则该位的结果值为 $1$，否则为 $0$。
• XOR 为按位异或运算，对等长二进制模式或二进制数的每一位执行逻辑异或操作。如果两个相应的二进制位不同（相异），则该位的结果值为 $1$，否则该位为 $0$。
• AND 为按位与运算，处理两个长度相同的二进制数，两个相应的二进制位都为 $1$，该位的结果值才为 $1$，否则为 $0$。

例如，我们将十进制数 $5$ 与十进制数 $3$ 分别进行 $OR、XOR$ 与 $AND$ 运算，可以得到如下结果：

0101 (十进制 5)             0101 (十进制 5)             0101 (十进制 5)             
OR 0011 (十进制 3)         XOR 0011 (十进制 3)         AND 0011 (十进制 3)             
 = 0111 (十进制 7)           = 0110 (十进制 6)           = 0001 (十进制 1) 

算法分析

本题是让我们选择 $[0, m]$ 之间的一个整数 $x_{0}$, 经过给定的 $n$ 次位运算, 使结果 ans 最大。

位运算的主要特点之一是在二进制表示下不进位。正因如此, 在 $x_{0}$ 可以任意选择的情况下, 参与位运算的各个位 (bit) 之间是独立无关的。换言之, 对于任意的 $k(0 \leq k<30$ ), “ans 的第 $k$ 位是几” 只与 “ $x_{0}$ 的第 $k$ 位是几” 有关, 与其他位无关。所以我们可以从高位到低位, 依次考虑 $x_{0}$ 的每一位填 0 还是填 1 。

$x_{0}$ 的第 $k$ 位应该填 1 , 当且仅当同时满足下列两个条件:

1. 已经填好的更高位构成的数值加上 $1 \ll k$ 以后不超过 $m$ 。
2. 用每个参数的第 $k$ 位参与位运算。若初值为 1 , 则 $n$ 次位运算后结果为 1 ; 若初值为 0 , 则 $n$ 次位运算后结果为 0 。

如果不满足上述条件, 要么填 1 会超过 $m$ 的范围, 要么填 1 不如填 0 更优。这 种情况下令 $x_{0}$ 的第 $k$ 位为 0 显然更好。确定 $x_{0}$ 的每一位以后, 自然可以得到 ans 的值。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<string>
using namespace std;
int n, m;
pair<string, int> a[100005];

int calc(int bit, int now) { // 用参数的第 bit 位进行 n 次运算
	for (int i = 1; i <= n; i++) {
		int x = a[i].second >> bit & 1;
		if (a[i].first == "AND") now &= x;
		else if (a[i].first == "OR") now |= x;
		else now ^= x;
	}
	return now;
}

int main() {
	cin >> n >> m;
	for (int i = 1; i <= n; i++) {
		char str[5];
		int x;
		scanf("%s%d", str, &x);
		a[i] = make_pair(str, x);
	}
	int val = 0, ans = 0;
	for (int bit = 29; bit >= 0; bit--) {
		int res0 = calc(bit, 0);
		int res1 = calc(bit, 1);
		if (val + (1 << bit) <= m && res0 < res1)
			val += 1 << bit, ans += res1 << bit;
		else
			ans += res0 << bit;
	}
	cout << ans << endl;
}

Solution

---

成对变换

通过计算可以发现, 对于非负整数 $n:$

当 $n$ 为偶数时, $n$ xor 1 等于 $n+1$ 。
当 $n$ 为奇数时, $n$ xor 1 等于 $n-1$ 。

因此, “ 0 与 1 ” “ 2 与 3 ” “ 4 与 5 ” $\cdots$ 关于 xor 1 运算构成 “成对变换”。

这一性质经常用于图论邻接表中边集的存储。在具有无向边 (双向边) 的图中把一对正反方向的边分别存储在邻接表数组的第 $n$ 与 $n+1$ 位置 (其中 $n$ 为偶数), 就可以通过 xor 1 的运算获得与当前边 $(x, y)$ 反向的边 $(y, x)$ 的存储位置。详细应用我们将在讲解邻接表时给出。

lowbit 运算

$\operatorname{lowbit}(n)$ 定义为非负整数 $n$ 在二进制表示下 “最低位的 1 及其后边所有的 0 ”构成的数值。例如 $n=10$ 的二进制表示为 $(1010)_{2}$, 则 $\operatorname{lowbit}(n)=2=(10)_{2}$ 。下面我们来推导 $\operatorname{lowbit}(n)$ 的公式。

$$\begin{align} n &= &xxxxx &\cdots xx&10000 \cdots 0000\\ \sim n &= &\tilde{x}\tilde{x}\tilde{x}\tilde{x}\tilde{x} &\cdots \tilde{x}\tilde{x} &01111\cdots1111\\ -n = \;\sim n + 1 &= &\tilde{x}\tilde{x}\tilde{x}\tilde{x}\tilde{x} &\cdots \tilde{x}\tilde{x} &10000\cdots0000\\ n \;\&\; (-n) = n \;\&\; (\sim n + 1)&= &00000 &\cdots00 &10000\cdots0000 \end{align}$$

设 $n>0, n$ 的第 $k$ 位是 1 , 第 $0 \sim k-1$ 位都是 0 。

为了实现 lowbit 运算, 先把 $n$ 取反, 此时第 $k$ 位变为 0 , 第 $0 \sim k-1$ 位都是 1。再令 $n=n+1$ ，此时因为进位, 第 $k$ 位变为 1 , 第 $0 \sim k-1$ 位都是 0 。

在上面的取反加 1 操作后, $n$ 的第 $k+1$ 到最高位恰好与原来相反, 所以 $n \;\&\;(\sim n+1)$ 仅有第 $k$ 位为 1 , 其余位都是 0 。而在补码表示下, $\sim n=-1-n$ , 因此:

$$\operatorname{lowbit}(n)=n \; \& \; (\sim n+1)=n \;\&\;(-n)$$

lowbit 运算配合 Hash 可以找出整数二进制表示下所有是 1 的位, 所花费的时间与 1 的个数同级。为了达到这一目的, 我们只需不断把 $n$ 赋值为 $n- \operatorname{lowbit}(n)$, 直至 $n=0$ 。例如 $n=9=(1001)_{2}$ , 则 $\operatorname{lowbit}(9)=1$ 。把 $n$ 赋值为 $9- \operatorname{lowbit}(9)=8=(1000)_{2}$ , 则 $\operatorname{lowbit}(8)=8=(1000)_{2}$ 。此时 $8-\operatorname{lowbit}(8)=0$ , 停止循环。在整个过程中我们减掉了 1 和 $8=(1000)_{2}$ 两个数, 它们恰好是 $n$ 每一位上的 1 后面补 0 得到的数值。取 1 和 8 的对数 $\log _{2} 1$ 和 $\log _{2} 8$, 即可得知 $n$ 的第 0 位和第 3 位是 1。因为 C++math.h 库的 $\log$ 函数是以 $\mathrm{e}$ 为底的实数运算, 并且复杂度常数较大, 所以我们需要预处理一个数组, 通过 Hash 的方法代替 $\log$ 运算。当 $n$ 较小时, 最简单的方法是直接建立一个数组 $H$, 令 $H\left[2^{k}\right]=k$, 如下面的程序所示。

const MAX_N = 1 << 20;
int H[MAX_N + 1];

for (int i = 0; i <= 20; ++i) H[1 << i] = i; //预处理

while (cin >> n) { // 对多次询问进行求解
	while (n > 0) {
		cout << H[n & -n] << ' ';
		n -= n & -n;
	}
	cout << endl;
}

稍微复杂但效率更高的方法是建立一个长度为 37 的数组 $H$, 令 $H\left[2^{k} \bmod 37\right]=$ $k$ 。这里利用了一个小的数学技巧: $\forall k \in[0,35], 2^{k} \bmod 37$ 互不相等, 且恰好取遍整数 1 ~ 36。修改之后的程序为:

// lowbit运算，找到二进制下所有是1的位
int H[37];
// 预处理
for (int i = 0; i < 36; i++) H[(1ll << i) % 37] = i;
// 对多次询问进行求解
while (cin >> n) {
	while (n > 0) {
		cout << H[(n & -n) % 37] << ' ';
		n -= n & -n;
	}
	cout << endl;
}

值得指出的是, lowbit 运算也是树状数组中的一个基本运算。

GCC 编译器还提供了一些内置函数, 可以高效计算 lowbit 以及二进制数中 1 的个数。不过, 这些函数并非 C 语言标准, 有的函数更是与机器或编译器版本相关的。另外, 部分竞赛禁止使用下划线开头的库函数, 故这些内置函数尽量不要随便使用。

//返回 x 的二进制表示下最低位的 1 后边有多少个 0
int __builtin_ctz(unsigned int x)
int __builtin_ctzll(unsigned long long x)

//返回 x 的二进制表示下有多少位为 1
int __builtin_popcount(unsigned int x)
int __builtin_popcountll(unsigned long long x)