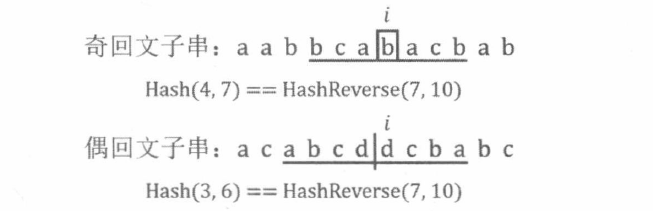基本数据结构 | Hash 哈希

参考《算法竞赛进阶指南》、AcWing题库

// 自定义 PairHash
struct PairHash {
    template<typename T, typename U> 
    size_t operator() (const pair<T, U> &v) const {
        size_t seed = 0;
        seed ^= hash<T>()(v.first) + 0x9e3779b9 + (seed << 6) + (seed >> 2);
        seed ^= hash<U>()(v.second) + 0x9e3779b9 + (seed << 6) + (seed >> 2);
        return seed;
    }
};

// 自定义 VectorHash
struct VectorHash {
    template<typename T> 
    size_t operator() (const vector<T> &v) const {
        size_t seed = 0;
        hash<T> hasher;
        for (auto x : v) {
            seed ^= hasher(x) + 0x9e3779b9 + (seed << 6) + (seed >> 2);
        }
        return seed;
    }
};

Hash

Hash 表又称为散列表, 一般由 Hash 函数 (散列函数) 与链表结构共同实现。与离散化思想类似, 当我们要对若干复杂信息进行统计时, 可以用 Hash 函数把这些复杂信息映射到一个容易维护的值域内。因为值域变简单、范围变小, 有可能造成两个不同的原始信息被 Hash 函数映射相同的值, 所以我们需要处理这种冲突情况。有一种称为 “开散列” 的解决方案是, 建立一个邻接表结构, 以 Hash 函数的值域作为表头数组 head, 映射后的值相同的原始信息被分到同一类, 构成一个链表接在对应的表头之后, 链表的节点上可以保存原始信息和一些统计数据。

Hash 表主要包括两个基本操作:

1. 计算 Hash 函数的值。
2. 定位到对应链表中依次遍历、比较。

无论是检查任意一个给定的原始信息在 Hash 表中是否存在, 还是更新它在 Hash 表中的统计数据, 都需要基于这两个基本操作进行。

当 Hash 函数设计较好时, 原始信息会被比较均匀地分配到各个表头之后, 从而使每次查找、统计的时间降低到 “原始信息总数除以表头数组长度”。若原始信息总数与表头数组长度都是 $\mathrm{O}(N)$ 级别且 Hash 函数分散均匀, 几乎不产生冲突, 那么每次查找、统计的时间复杂度期望为 $O(1)$ 。

例如, 我们要在一个长度为 $N$ 的随机整数序列 $A$ 中统计每个数出现了多少次。当 数列 $A$ 中的值都比较小时, 我们可以直接用一个数组计数（建立一个大小等于值域的数组进行统计和映射, 其实就是最简单的 Hash 思想)。当数列 $A$ 中的值很大时, 我们可以把 $A$ 排序后扫描统计。这里我们换一种思路, 尝试一下 Hash 表的做法。

设计 Hash 函数为 $H(x)=(x \bmod P)+1$, 其中 $P$ 是一个比较大的质数, 但不超过 $N$ 。显然, 这个 Hash 函数把数列 $A$ 分成 $P$ 类, 我们可以依次考虑数列中的每个数 $A[i]$, 定位到 $head[H(A[i])]$ 这个表头所指向的链表。如果该链表中不包含 $A[i]$, 我们就在表头后揷入一个新节点 $A[i]$, 并在该节点上记录 $A[i]$ 出现了 1 次, 否则我们就直接找到已经存在的 $A[i]$ 节点将其出现次数加 1 。因为整数序列 $A$ 是随机的, 所以最终所有的 $A[i]$ 会比较均匀地分散在各个表头之后, 整个算法的时间复杂度可以近似达到 $O(N)$ 。

上面的例子是一个非常简单的 Hash 表的直观应用。对于非随机的数列, 我们可以 设计更好的 Hash 函数来保证其时间复杂度。同样地, 如果我们需要维护的是比大整数复杂得多的信息的某些性质 (如是否存在、出现次数等), 也可以用 Hash 表来解决。 字符串就是一种比较一般化的信息, 在本节的后半部分, 我们将会介绍一个程序设计竞赛中极其常用的字符串 Hash 算法。

---

例题

137. 雪花雪花雪花

有 $N$ 片雪花，每片雪花由六个角组成，每个角都有长度。

第 $i$ 片雪花六个角的长度从某个角开始顺时针依次记为 $a_{i,1},a_{i,2},…,a_{i,6}$。

因为雪花的形状是封闭的环形，所以从任何一个角开始顺时针或逆时针往后记录长度，得到的六元组都代表形状相同的雪花。

例如 $a_{i,1},a_{i,2},…,a_{i,6}$ 和 $a_{i,2},a_{i,3},…,a_{i,6}，a_{i,1}$ 就是形状相同的雪花。

$a_{i,1},a_{i,2},…,a_{i,6}$ 和 $a_{i,6},a_{i,5},…,a_{i,1}$ 也是形状相同的雪花。

我们称两片雪花形状相同，当且仅当它们各自从某一角开始顺时针或逆时针记录长度，能得到两个相同的六元组。

求这 $N$ 片雪花中是否存在两片形状相同的雪花。

输入格式

第一行输入一个整数 $N$，代表雪花的数量。

接下来 $N$ 行，每行描述一片雪花。

每行包含 $6$ 个整数，分别代表雪花的六个角的长度（这六个数即为从雪花的随机一个角顺时针或逆时针记录长度得到）。

同行数值之间，用空格隔开。

输出格式

如果不存在两片形状相同的雪花，则输出：

No two snowflakes are alike.

如果存在两片形状相同的雪花，则输出：

Twin snowflakes found.

数据范围

$1 \le N \le 100000$,
$0 \le a_{i,j} <10000000$

输入样例：

2
1 2 3 4 5 6
4 3 2 1 6 5 

输出样例：

Twin snowflakes found. 

算法分析

定义 Hash 函数 $H\left(a_{i, 1}, a_{i, 2}, \cdots, a_{i, 6}\right)=\left(\sum_{j=1}^{6} a_{i, j}+\prod_{j=1}^{6} a_{i, j}\right) \bmod P$, 其中 $P$ 是我们自己选取的一个较大的质数。显然, 对于两片形状相同的雪花, 它们六个角的长度之和、长度之积都相等, 因此它们的 Hash 函数值也相等。

建立一个 Hash 表, 把 $N$ 片雪花依次揷入。对于每片雪花 $a_{i, 1}, a_{i, 2}, \cdots, a_{i, 6}$, 我们直接扫描表头 $H\left(a_{i, 1}, a_{i, 2}, \cdots, a_{i, 6}\right)$ 对应的链表, 检查是否存在与 $a_{i, 1}, a_{i, 2}, \cdots, a_{i, 6}$ 形状相同的雪花即可。对于随机数据, 期望的时间复杂度为 $O\left(N^{2} / P\right)$; 取 $P$ 为最接近 $N$ 的质数, 期望的时间复杂度为 $O(N)$ 。在下一节中, 我们将学习循环同构串的 “最小表示法”, 进一步提高判断两片雪花形状是否相同的效率。

Solution

---

字符串哈希

下面介绍的字符串 Hash 函数把一个任意长度的字符串映射成一个非负整数, 并且其冲突概率几乎为零。

取一固定值 $P$, 把字符串看作 $P$ 进制数, 并分配一个大于 0 的数值, 代表每种字符。一般来说, 我们分配的数值都远小于 $P$ 。例如, 对于小写字母构成的字符串, 可以 令 $a=1, b=2, \cdots, z=26$ 。取一固定值 $M$, 求出该 $P$ 进制数对 $M$ 的余数, 作为该字符串的 Hash 值。

一般来说, 我们取 $P=131$ 或 $P=13331$, 此时 Hash 值产生冲突的概率极低, 只要 Hash 值相同, 我们就可以认为原字符串是相等的。通常我们取 $M=2^{64}$, 即直接使用 unsigned long long 类型存储这个 Hash 值, 在计算时不处理算术溢出问题, 产生溢出时相当于自动对 $2^{64}$ 取模, 这样可以避免低效的取模 (mod) 运算。

除了在极特殊构造的数据上, 上述 Hash 算法很难产生冲突, 一般情况下上述 Hash 算法完全可以出现在题目的标准解答中。我们还可以多取一些恰当的 $P$ 和 $M$ 的值（例如大质数), 多进行几组 Hash 运算, 当结果都相同时才认为原字符串相等, 就更加难 以构造出使这个 Hash 产生错误的数据。

对字符串的各种操作, 都可以直接对 $P$ 进制数进行算术运算反映到 Hash 值上。如果我们已知字符串 $S$ 的 Hash 值为 $H(S)$, 那么在 $S$ 后添加一个字符 $c$ 构成 的新字符串 $S+c$ 的 Hash 值就是 $H(S+c)=(H(S) * P+ value [c]) \bmod M$ 。其中乘 $P$ 就相当于 $P$ 进制下的左移运算, $value [c]$ 是我们为 $c$ 选定的代表数值。

如果我们已知字符串 $S$ 的 Hash 值为 $H(S)$, 字符串 $S+T$ 的 Hash 值为 $H(S+$ $T$ ), 那么字符串 $T$ 的 Hash 值 $H(T)=\left(H(S+T)-H(S) * P^{\text {length }(T)}\right) \bmod M$ 。这就相当于通过 $P$ 进制下在 $S$ 后边补 0 的方式, 把 $S$ 左移到与 $S+T$ 的左端对齐, 然后 二者相减就得到了 $H(T)$ 。

例如, $S=\text{``abc"}$ , $c=\text{``d"}$ , $T=\text{``xyz"}$ , 则:

$S$ 表示为 $P$ 进制数: 123

$H(S)=1 * P^{2}+2 * P+3$

$H(S+c)=1 * P^{3}+2 * P^{2}+3 * P+4=H(S) * P+4$

$S+T$ 表示为 $P$ 进制数: 123242526

$H(S+T)=1 * P^{5}+2 * P^{4}+3 * P^{3}+24 * P^{2}+25 * P+26$

$S$ 在 $P$ 进制下左移 $length(T)$ 位: 123000

二者相减就是 $T$ 表示为 $P$ 进制数: 242526

$H(T)=\left(H(S+T)-H(S) * P^{\text {length }(T)}\right)=H(S+T)-\left(1 * P^{2}+2 * P+3\right) * P^{3}=24 * P^{2}+25 * P+26$

根据上面两种操作, 我们可以通过 $O(N)$ 的时间预处理字符串所有前缀 Hash 值, 并在 $O(1)$ 的时间内查询它的任意子串的 Hash 值。

字符串哈希例题

138. 兔子与兔子

很久很久以前，森林里住着一群兔子。

有一天，兔子们想要研究自己的 DNA 序列。

我们首先选取一个好长好长的 DNA 序列（小兔子是外星生物，DNA 序列可能包含 $26$ 个小写英文字母）。

然后我们每次选择两个区间，询问如果用两个区间里的 DNA 序列分别生产出来两只兔子，这两个兔子是否一模一样。

注意两个兔子一模一样只可能是他们的 DNA 序列一模一样。

输入格式

第一行输入一个 DNA 字符串 $S$。

第二行一个数字 $m$，表示 $m$ 次询问。

接下来 $m$ 行，每行四个数字 $l_1, r_1, l_2, r_2$，分别表示此次询问的两个区间，注意字符串的位置从 $1$ 开始编号。

输出格式

对于每次询问，输出一行表示结果。

如果两只兔子完全相同输出 Yes，否则输出 No（注意大小写）。

数据范围

$1 \le length(S),m \le 1000000$

输入样例：

aabbaabb
3
1 3 5 7
1 3 6 8
1 2 1 2 

输出样例：

Yes
No
Yes 

算法分析

记我们选取的 DNA 序列为 $S$, 根据我们刚才提到的字符串 Hash 算法, 设 $F[i]$ 表示前缀子串 $S[1 \sim i]$ 的 Hash 值, 有 $F[i]=F[i-1] * 131+\left(S[i]- \text{`a'} +1\right)$ 。

于是可以得到任一区间 $[l, r]$ 的 Hash 值为 $F[r]-F[l-1] * 131^{r-l+1}$ 。当两个区间的 Hash 值相同时, 我们就认为对应的两个子串相等。整个算法的时间复杂度为 $\mathrm{O}(|S|+Q)$ 。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
char s[1000010]; 
unsigned long long f[1000010], p[1000010];
int main() {
	scanf("%s", s + 1);
	int n, q;
	n = strlen(s + 1);
	cin >> q;
	p[0] = 1; // 131^0
	for (int i = 1; i <= n; i++) {
		f[i] = f[i-1] * 131 + (s[i]-'a'+1); // hash of 1~i
		p[i] = p[i-1] * 131; // 131^i
	}
	for (int i = 1; i <= q; i++) {
		int l1, r1, l2, r2;
		scanf("%d%d%d%d", &l1, &r1, &l2, &r2);
		if (f[r1] - f[l1-1] * p[r1-l1+1] == // hash of l1~r1
			f[r2] - f[l2-1] * p[r2-l2+1]) { // hash of l2~r2
			puts("Yes");
		} else {
			puts("No");
		}
	}
}

Solution

---

139. 回文子串的最大长度

如果一个字符串正着读和倒着读是一样的，则称它是回文的。

给定一个长度为 $N$ 的字符串 $S$，求他的最长回文子串的长度是多少。

输入格式

输入将包含最多 $30$ 个测试用例，每个测试用例占一行，以最多 $1000000$ 个小写字符的形式给出。

输入以一个以字符串 END 开头的行表示输入终止。

输出格式

对于输入中的每个测试用例，输出测试用例编号和最大回文子串的长度（参考样例格式）。

每个输出占一行。

输入样例：

abcbabcbabcba
abacacbaaaab
END 

输出样例：

Case 1: 13
Case 2: 6 

算法分析

写几个回文串观察它们的性质, 我们可以发现回文串分为两类:

1. 奇回文串 $A[1 \sim M]$, 长度 $M$ 为奇数, 并且 $A[1 \sim M / 2+1]=\operatorname{reverse}(A[M / 2+1 \sim M])$, 它的中心点是一个字符。其中 $\operatorname{reverse}(A)$ 表示把字符串 $\mathrm{A}$ 倒过来。
2. 偶回文串 $B[1 \sim M]$, 长度 $M$ 为偶数, 且 $B[1 \sim M / 2]=\operatorname{reverse}(B[M / 2+1 \sim M])$, 它的中心点是两个字符之间的夹缝。

于是在本题中, 我们可以枚举 $S$ 的回文子串的中心位置 $i=1 \sim N$, 看从这个中心位置出发向左右两侧最长可以扩展出多长的回文串。也就是说:

1. 求出一个最大的整数 $p$ 使得 $S[i-p \sim i]=\operatorname{reverse}(S[i \sim i+p])$, 那么以 $i$ 为中心的最长奇回文子串的长度就是 $2 * p+1$ 。
2. 求出一个最大的整数 $q$ 使得 $S[i-q \sim i-1]=\operatorname{reverse}(S[i \sim i+q-1])$, 那么 以 $i-1$ 和 $i$ 之间的夹缝为中心的最长偶回文子串的长度就是 $2 * q$ 。

根据上一道题目, 我们已经知道在 $O(N)$ 预处理前缀 Hash 值后, 可以 $O(1)$ 计算任意子串的 Hash 值。类似地, 我们可以倒着做一遍预处理, 就可以 $O(1)$ 计算任意子串倒着读的 Hash 值。于是我们可以对 $p$ 和 $q$ 进行二分答案, 用 Hash 值 $\mathrm{O}(1)$ 比较一个正着读的子串和一个倒着读的子串是否相等, 从而在 $\mathrm{O}(\log N)$ 时间内求出最大的 $p$ 和 $q$ 。在枚举过的所有中心位置对应的奇、偶回文子串长度中取 max 就是整道题目的答案, 时间复杂度为 $\mathrm{O}(N \log N)$ 。

有一个名为 Manacher 的算法可以 $O(N)$ 求解该问题, 感兴趣的读者可以自行查阅相关资料。

Solution

---

140. 后缀数组

后缀数组 (SA，Suffix Array) 是一种重要的数据结构，通常使用倍增或者 DC3 算法实现，这超出了我们的讨论范围。

在本题中，我们希望使用快排、Hash 与二分实现一个简单的 $O(nlog^2n)$ 的后缀数组求法。

详细地说，给定一个长度为 $n$ 的字符串 $S$（下标 $0 \sim n-1$），我们可以用整数 $k$($0 \le k < n$) 表示字符串 $S$ 的后缀 $S(k \sim n-1)$。

把字符串 $S$ 的所有后缀按照字典序排列，排名为 $i$ 的后缀记为 $SA[i]$。

额外地，我们考虑排名为 $i$ 的后缀与排名为 $i-1$ 的后缀，把二者的最长公共前缀的长度记为 $Height[i]$。

我们的任务就是求出 $SA$ 与 $Height$ 这两个数组。

输入格式

输入一个字符串，其长度不超过 $30$ 万。

字符串由小写字母构成。

输出格式

第一行为数组 $SA$，相邻两个整数用 $1$ 个空格隔开。

第二行为数组 $Height$，相邻两个整数用 $1$ 个空格隔开，我们规定 $Height[1]=0$。

输入样例：

ponoiiipoi 

输出样例：

9 4 5 6 2 8 3 1 7 0
0 1 2 1 0 0 2 1 0 2 

算法分析

$S$ 的所有后缀的总长度在 $O\left(n^{2}\right)$ 级别, 如果我们直接对这 $n$ 个后缀进行快排, 对 于两个字符串的大小比较采取逐字符扫描的方式, 最坏情况下时间复杂度将达到 $O\left(n^{2} \log n\right)$ 。

在上一道题目中, 我们已经知道如何求出一个字符串的所有前缀 Hash 值, 并进一步在 $O(1)$ 的时间内查询任意一个区间子串的 Hash 值。所以在快速排序需要比较两个后缀 $p$ 和 $q$ 时, 我们就可以使用二分法, 每次二分时利用 Hash 值 $O(1)$ 地比较 $S[p \sim p+m i d-1]$ 与 $S[q \sim q+m i d-1]$ 这两段是否相等, 最终求出 $S[p \sim n]$ 与 $S[q \sim n]$ 的最长公共前缀的长度, 记为 $len$ 。于是 $S[p+l e n]$ 和 $S[q+l e n]$ 就是这两个后缀第一个不相等的位置, 直接比较这两个字符的大小就可以确定 $S[p \sim n]$ 与 $S[q \sim n]$ 的大小关系。从而每次比较的总复杂度就是 $O(\log n)$, 整个快排求出 $SA$ 数组的过程的复杂度就是 $O\left(n \log ^{2} n\right)$ 。在排序完成后, 我们对于每对排名相邻的后缀执行与上述相同的二分过程, 就可以求出 $Height$ 数组了。

Solution