算法代码笔记

算法基础

快速排序

void quick_sort(int q[], int l, int r) {
  if (l >= r) return;
  int i = l - 1, j = r + 1;  //注意i,j起始位置是在l,r的越界位置
  int x = q[l + r >> 1];
  while (i < j) {
    do ++i; while (q[i] < x);
    do --j; while (q[j] > x);
    if (i < j) swap(q[i], q[j]);
  }
  quick_sort(q, l, j);
  quick_sort(q, j + 1, r);
}

void quickSort(int q[], int l, int r) {
  if (l >= r) return;
  int i = l - 1, j = r + 1;
  int x = q[l + r >> 1];
  while (i < j) {
    while (q[++i] < x);
    while (q[--j] > x);
    if (i < j) swap(q[i], q[j]);
  }
  quickSort(q, l, j);
  quickSort(q, j + 1, r);
}

快速选择

int quick_select(int q[], int l, int r, int k) {
  if (l >= r) return q[l];
  int i = l - 1, j = r + 1;
  int x = q[l + r >> 1];
  while (i < j) {
    while (q[++i] < x);
    while (q[--j] > x);
    if (i < j) swap(q[i], q[j]);
  }
  int n = j - l + 1;  // 已确定最小的n个数，在q[l~j]里面
  if (n >= k) return quick_select(q, l, j, k);
  return quick_select(q, j + 1, r, k - n);  //还差k-n个数需要确定
}

归并排序

class Solution {
public:
    vector<int> temp;
    vector<int> sortArray(vector<int>& nums) {
        temp.resize(nums.size());
        mergeSort(nums, 0, nums.size() - 1);
        return nums;
    }
    void mergeSort(vector<int>&nums, int l, int r){
        if (l >= r) return;

        int mid = l + r >> 1;
        mergeSort(nums, l, mid);
        mergeSort(nums, mid + 1, r);

        
        int i = l, j = mid + 1, k = l;
        while (i <= mid && j <= r) {
            if (nums[i] <= nums[j]) temp[k++] = nums[i++]; 
            else temp[k++] = nums[j++];
        }
        while (i <= mid) temp[k++] = nums[i++];
        while (j <= r) temp[k++] = nums[j++];

        for (int i = l; i <= r; ++i) nums[i] = temp[i];
    }
};

整数二分

bool check(int x) { /* ... */
}  // 检查x是否满足某种性质

// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用：
int bsearch_1(int l, int r) {
  while (l < r) {
    int mid = l + r >> 1;
    if (check(mid))
      r = mid;  // check()判断mid是否满足性质
    else
      l = mid + 1;
  }
  return l;
}
// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用：
int bsearch_2(int l, int r) {
  while (l < r) {
    int mid = l + r + 1 >> 1;
    if (check(mid))
      l = mid;
    else
      r = mid - 1;
  }
  return l;
}

浮点数二分

bool check(double x) { /* ... */
}  // 检查x是否满足某种性质

double bsearch_3(double l, double r) {
  const double eps = 1e-6;  // eps 表示精度，取决于题目对精度的要求
  while (r - l > eps) {
    double mid = (l + r) / 2;
    if (check(mid))
      r = mid;
    else
      l = mid;
  }
  return l;
}

高精度加法

vector存储数时，低位在头，高位在尾，这样有进位时push_back()效率高

// C = A + B, A >= 0, B >= 0
vector<int> add(vector<int> &A, vector<int> &B) {
  if (A.size() < B.size()) return add(B, A);

  vector<int> C;
  int t = 0;
  for (int i = 0; i < A.size(); i++) {
    t += A[i];
    if (i < B.size()) t += B[i];
    C.push_back(t % 10);
    t /= 10;
  }

  if (t) C.push_back(t);
  return C;
}

高精度减法

// C = A - B, 满足A >= B, A >= 0, B >= 0
vector<int> sub(vector<int> &A, vector<int> &B) {
  vector<int> C;
  for (int i = 0, t = 0; i < A.size(); i++) {
    t = A[i] - t;
    if (i < B.size()) t -= B[i];
    C.push_back((t + 10) % 10);
    if (t < 0)
      t = 1;
    else
      t = 0;
  }

  while (C.size() > 1 && C.back() == 0) C.pop_back();
  return C;
}

高精度*低精度

// C = A * b, A >= 0, b >= 0
vector<int> mul(vector<int> &A, int b) {
  vector<int> C;

  int t = 0;
  for (int i = 0; i < A.size() || t; i++) {
    if (i < A.size()) t += A[i] * b;
    C.push_back(t % 10);
    t /= 10;
  }

  while (C.size() > 1 && C.back() == 0) C.pop_back();

  return C;
}

高精度/低精度

// A / b = C ... r, A >= 0, b > 0
vector<int> div(vector<int> &A, int b, int &r) {
  vector<int> C;
  r = 0;
  for (int i = A.size() - 1; i >= 0; i--) {
    r = r * 10 + A[i];
    C.push_back(r / b);
    r %= b;
  }
  reverse(C.begin(), C.end());
  while (C.size() > 1 && C.back() == 0) C.pop_back();
  return C;
}

一维前缀和

1
2
3

//i从1开始
S[i] = a[1] + a[2] + ... a[i]
a[l] + ... + a[r] = S[r] - S[l - 1]

二维前缀和

1
2
3

S[i, j] = 第i行j列格子左上部分所有元素的和
以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵的和为：
S[x2, y2] - S[x1 - 1, y2] - S[x2, y1 - 1] + S[x1 - 1, y1 - 1]

一维差分

//给区间[l, r]中的每个数加上c：
void insert(int l,int r,int c){
    B[l] += c; 
    B[r + 1] -= c;
}

二维差分

//给以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵中的所有元素加上c：
void insert(int x1, int y1, int x2, int y2, int c) {
  b[x1][y1] += c;
  b[x1][y2 + 1] -= c;
  b[x2 + 1][y1] -= c;
  b[x2 + 1][y2 + 1] += c;

位运算

1 2	求n的第k位数字: n >> k & 1 返回n的最后一位1：lowbit(n) = n & -n

双指针

for (int i = 0, j = 0; i < n; i ++ )
{
    while (j <= i && check(i, j)) j ++ ;

    // 具体问题的逻辑
}
寻找单调性
常见问题分类：
    (1) 对于一个序列，用两个指针维护一段区间
    (2) 对于两个序列，维护某种次序，比如归并排序中合并两个有序序列的操作

离散化

vector<int> alls;                // 存储所有待离散化的值
sort(alls.begin(), alls.end());  // 将所有值排序
alls.erase(unique(alls.begin(), alls.end()), alls.end());  // 去掉重复元素

// 二分求出x对应的离散化的值
int find(int x)  // 找到第一个大于等于x的位置
{
  int l = 0, r = alls.size() - 1;
  while (l < r) {
    int mid = l + r >> 1;
    if (alls[mid] >= x)
      r = mid;
    else
      l = mid + 1;
  }
  return r + 1;  // 映射到1, 2, ...n
}

区间合并

// 将所有存在交集的区间合并
using PII = pair<int, int>;
void mergeSegs(vector<PII> &segs) {
  sort(segs.begin(), segs.end());
  vector<PII> ans;
  int l = -2e9, r = -2e9;  // l,r初始值要小于区间可能范围
  for (auto seg : segs) {
    if (r < seg.first) {  //当前区间和[l,r]维护区间不相交
      if (l != -2e9) ans.push_back({l, r});
      l = seg.first;  //更新l
    }
    r = max(r, seg.second);  //更新r,相交不相交都会更新r
  }
  if (l != -2e9) ans.push_back({l, r});
  segs = ans;
}

数据结构

单链表

int head, e[N], ne[N], idx;
void init() {
  head = -1;
  idx = 0;
}
void insertHead(int x) {}
void insertAfter(int k, int x) {  //在第k个插入的数后插入数x
  if (k == 0) {                   //向链表头插入数x
    e[idx] = x, ne[idx] = head, head = idx++;
  }
  e[idx] = x, ne[idx] = ne[k], ne[k] = idx++;
}
void removeAfter(int k) {  //删除第k个插入的数的后面的数
  if (k == 0) {            //删除单链表头节点
    head = ne[head];
  }
  ne[k] = ne[ne[k]];
}

双链表

int e[N], l[N], r[N], idx;  // 0,1存储点分别表示头尾哨兵head,tail,数据从2开始存储
void init() {
  r[0] = 1, l[1] = 0;
  idx = 2;
}
void insertAfter(int k, int x) {  //在节点k(即存储下标k)后插入数x
  e[idx] = x, l[idx] = k, r[idx] = r[k];
  r[k] = idx, l[r[idx]] = idx;
  ++idx;
}
void removeK(int k) {
  l[r[k]] = l[k];
  r[l[k]] = r[k];
}

栈

int stk[N], tt = 0;  // tt表示栈顶，0表示栈空，从1开始存储
void push(int x) { stk[++tt] = x; }
void pop() { --tt; }
int top() { return stk[tt]; }
bool empty() { return tt == 0; }

队列

int q[N], hh = 0, tt = -1;  //从0开始存储数据
void push() { q[++tt] = x; }
void pop() { ++hh; }
void front() { return q[hh]; }
bool empty() { return hh > tt; }

循环队列

int q[N], hh = 0, tt = 0;
void push(int x) {
  q[tt++] = x;
  if (tt == N) tt = 0;
}
void pop() {
  hh++;
  if (hh == N) hh = 0;
}
int front() { return q[hh]; }
bool empty() { return hh == tt; }

单调栈

常见模型：找出每个数左边离它最近的比它大/小的数

int tt = 0;  //从1开始存储，0表示栈空
for (int i = 1; i <= n; ++i) {
    while(tt&&check(stk[tt],data[i])--tt;
    stk[++tt]=i;//一般存储的是下标
}

单调队列

int hh = 0, tt = -1;
for (int i = 0; i < n; ++i) {
  while (hh <= tt && check_out(q[hh])) ++hh;  //检查当前队列队头hh要不要更新
  while (hh <= tt && check(q[tt], data[i])) --tt;
  q[++tt] = i;
}

KMP

s是长文本串，长度为n，范围[1,2,3…n]
p是模式串，长度为m，范围[1,2,3…m]
s,p都是从下标1开始存储的！
ne[1]=0
next[j] 表示所有 p[1~j] 的相等的前缀和后最中长度的最大值

//求模式串p的next数组
for (int i = 2, j = 0; i <= m; ++i) {
  while (j && p[i] != p[j + 1]) j = ne[j];  //当前[1，j]是匹配的，长度为j
  if (p[i] == p[j + 1])
    ++j;  //找到了匹配前缀，匹配长度+1；如果没找到，则ne[i]=0
  ne[i] = j;  //更新
}
//进行匹配
for (int i = 1, j = 0; i <= n; ++i) {
  while (j && s[i] != p[j + 1]) j = ne[j];
  if (s[i] == p[j + 1]) ++j;
  if (j == m) {
    j = ne[j];  //进行下一轮匹配
                //匹配成功后的逻辑
  }
}

Trie 字典树

0号点既是根节点，又是空节点
son[ i ][ x ]存储字典树中当前节点 i 的值为x的子节点的位置
cnt[ i ]存储以当前节点 i 结尾的单词数量

int son[N][26], cnt[N], idx;
void insert(string &str) {
  int p = 0;  //从根节点开始
  for (int i = 0; i < str.size(); ++i) {
    int u = str[i] - 'a';
    if (son[p][u] == 0)
      son[p][u] = ++idx;  // son[p][u]指向空节点，即不存在，直接创建
    p = son[p][u];        //跳转
  }
  ++cnt[p];
}
int query(string &str) {
  int p = 0;
  for (int i = 0; i < str.size(); ++i) {
    int u = str[i] - 'a';
    if (son[p][u] == 0) return 0;
    p = son[p][u];
  }
  return cnt[p];
}

并查集

朴素并查集

  int fa[N];
  void init() {
      for (int i = 1; i <= n; ++i) fa[i] = i;
  }
  
  int find(int x) {
      if (fa[x] == x) return x;
      return fa[x] = find(fa[x]);
  }
  
  bool merge(int x, int y) {
      int rootx = find(x), rooty = find(y);
      if (rootx == rooty) return false;
      fa[rootx] = rooty;
      return true;
  }

- 维护size的边带权并查集

  ```CPP
  int fa[N], d[N], size[N];
  
  void init() {
    for (int i = 1; i <= n; ++i) {
      fa[i] = i;
      d[i] = 0;
      size[i] = 1;
    }
  }
  
  int find(int x) {
    if (fa[x] == x) return x;
  
    int root = find(fa[x]);  // 递归计算集合代表
    d[x] += d[fa[x]];        // 维护d数组——对边权求和
    return fa[x] = root;     // 路径压缩
  }
  
  bool merge(int x, int y) {
    x = find(x), y = find(y);
    if (x == y) return false;
  
    fa[x] = y;
    d[x] = newDist;  //根据具体问题初始化
    size[y] += size[x];
    return true;
  }

堆

h[N]存储堆中的值，范围：[1,2,3,…,n]，从1开始存储，h[1]：堆顶
节点u ：
- 左孩子：2u
- 右孩子：2u+1
- 父节点：u/2
ph[k]：存储第k个插入的点在堆heap中的位置
hp[k]：存储堆heap中下标为k的位置处的节点是第几个插入的

int h[N], ph[N], hp[N], idx;
void heapSwap(int a, int b) {
  swap(ph[hp[a]], ph[hp[b]]);
  swap(hp[a], hp[b]);
  swap(h[a], h[b]);
}
void up(int u) {
  while (u / 2 && h[u] < h[u / 2]) {
    heapSwap(u, u / 2);
    u /= 2;
  }
}
void down(int u) {
  int t = u;
  if (2 * u <= idx && h[t] > h[2 * u]) t = 2 * u;
  if (2 * u + 1 <= idx && h[t] > h[2 * u + 1]) t = 2 * u + 1;
  if (t != u) {
    heapSwap(t, u);
    down(t);
  }
}
void buildHeap() {
  for (int i = n / 2; i; i--) down(i);
}

一般哈希

拉链法

int h[N], e[N], ne[N], idx;
void insert(int x) {
  int k = (x % N + N) % N;
  e[idx] = x;
  ne[idx] = h[k];
  h[k] = idx++;
}
bool find(int x) {
  int k = (x % N + N) % N;
  for (int i = h[k]; ~i; i = ne[i]) {
    if (e[i] == x) return true;
  }
  return false;
}

开放寻址法

const int null = 0x3f3f3f3f;
int h[N];
int find(int x) {
  int t = (x % N + N) % N;
  while (h[t] != null && h[t] != x) {
    ++t;
    if (t == N) t = 0;
  }
  return t;
}
void init() { memset(h, 0x3f, sizeof(h)); }

字符串前缀哈希

核心思想：将字符串看成P进制数，P的经验值是 131或 13331，取这两个值的冲突概率低
小技巧：取模的数用 2^64，这样直接用 unsigned long long存储，溢出的结果就是取模的结果
h[0]=0，h[k]表示串长为k的前缀子串的哈希值，前缀和思想
p[k]表示p^k mod 2^64

using ULL = unsigned long long;
const int P = 131;
ULL h[N], p[N];
void init() {
  p[0] = 1;
  for (int i = 1; i <= n; ++i) {
    p[i] = p[i - 1] * P;
    h[i] = h[i - 1] * P + str[i];
  }
}
ULL hashsubstr(int l, int r) { return h[r] - h[l - 1] * p[r - l + 1]; }

C++ 常用STL

vector, 变长数组，倍增的思想

size()  返回元素个数
empty()  返回是否为空
clear()  清空
front()/back()
push_back()/pop_back()
begin()/end()
[]
支持比较运算，按字典序

pair<int, int>

1
2
3

first, 第一个元素
second, 第二个元素
支持比较运算，以first为第一关键字，以second为第二关键字（字典序）

string，字符串

size()/length()  返回字符串长度
empty()
clear()
substr(起始下标，(子串长度))  返回子串
c_str()  返回字符串所在字符数组的起始地址

queue, 队列

size()
empty()
push()  向队尾插入一个元素
front()  返回队头元素
back()  返回队尾元素
pop()  弹出队头元素

priority_queue, 优先队列，默认是大根堆

size()
empty()
push()  插入一个元素
top()  返回堆顶元素
pop()  弹出堆顶元素
定义成小根堆的方式：priority_queue<int,vector<int>, greater<int>> q;

stack, 栈

size()
empty()
push()  向栈顶插入一个元素
top()  返回栈顶元素
pop()  弹出栈顶元素

deque, 双端队列

size()
empty()
clear()
front()/back()
push_back()/pop_back()
push_front()/pop_front()
begin()/end()
[]

+ set, map, multiset, multimap, 基于平衡二叉树（红黑树），动态维护有序序列

  ```cpp
  size()
  empty()
  clear()
  begin()/end()
  ++, -- 返回前驱和后继，时间复杂度 O(logn)

size()
empty()
clear()
begin()/end()
++, -- 返回前驱和后继，时间复杂度 O(logn)

size()
empty()
clear()
begin()/end()
++, -- 返回前驱和后继，时间复杂度 O(logn)

set/multiset

insert()  插入一个数
find()  查找一个数
count()  返回某一个数的个数
erase()
    (1) 输入是一个数x，删除所有x   O(k + logn)
    (2) 输入一个迭代器，删除这个迭代器
lower_bound()/upper_bound()
    lower_bound(x)  返回大于等于x的最小的数的迭代器
    upper_bound(x)  返回大于x的最小的数的迭代器

map/multimap

insert()  插入的数是一个pair
erase()  输入的参数是pair或者迭代器
find()
[]  注意multimap不支持此操作。 时间复杂度是 O(logn)
lower_bound()/upper_bound()

unordered_set, unordered_map, unordered_multiset, unordered_multimap, 哈希表

1 2	和上面类似，增删改查的时间复杂度是 O(1) 不支持 lower_bound()/upper_bound()，迭代器的++，--

bitset, 圧位

bitset<10000> s;
~, &, |, ^
>>, <<
==, !=
[]

count()  返回有多少个1

any()  判断是否至少有一个1
none()  判断是否全为0

set()  把所有位置成1
set(k, v)  将第k位变成v
reset()  把所有位变成0
flip()  等价于~
flip(k) 把第k位取反

搜索与图论

数与图的存储

树是一种特殊的图，与图的存储方式相同。

对于无向图中的边ab，存储两条有向边a->b, b->a。因此我们可以只考虑有向图的存储。

邻接矩阵：g[a][b]

邻接表

// 对于每个点k，开一个单链表，存储k所有可以走到的点。h[k]存储这个单链表的头结点
//N是点数，M是边数,无向图M=N*2
int h[N], e[M], ne[M], idx;
void init(){
    idx = 0;
    memset(h, -1, sizeof h);  
}
void add(int a, int b){
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}

数与图的遍历

时间复杂度O(V+E)

DFS,深度优先遍历,递归

int dfs(int u){
    visited[u] = true; // visited[u] 表示点u已经被遍历过
    for (int i = h[u]; ~i; i = ne[i]){
        int j = e[i];
        if (visited[j]==false) {
            dfs(j);
        }
    }
}

BFS,广度优先遍历，队列辅助

int bfs(int u) {
  queue<int> q;
  visited[u] = true;
  q.push(u);
  while (q.size()) {
    auto t = q.front();
    q.pop();
    for (int i = h[t]; ~i; i = ne[i]) {
      int j = e[i];
      if (visited[j] == false) {
        dis[j] = dis[t] + 1;  //记录距离
        prev[j] = t;          //记录前一个点
        visited[j] = true;
        q.push(j);
      }
    }
  }
}

BFS状态转移

unordered_map<string, int> d;
unordered_map<string, bool> visited;
string start, endstr = "12345678x";
bool bfs(string start) {
  queue<string> q;
  visited[start] = true;
  d[start] = 0;
  q.push(start);
  while (q.size()) {
    auto u = q.front();
    q.pop();
    if (u == endstr) return true;  //如果已经是目标状态

    int k = u.find('x');
    int ux = k / 3, uy = k % 3;  //二维坐标转一维坐标
    //状态转移
    for (int i = 0; i < 4; ++i) {
      int vx = ux + dx[i], vy = uy + dy[i];
      if (vx >= 0 && vx < 3 && vy >= 0 && vy < 3) {
        string v = u;
        swap(v[k], v[vx * 3 + vy]);
        if (visited[v] == false) {  //如果当前状态未曾到达过
          d[v] = d[u] + 1;
          visited[v] = true;
          q.push(v);
        }
      }
    }
  }
  return false;
}

拓扑排序

BFS队列入度拓扑排序

时间复杂度 $O(V+E)$

vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {
    vector<int> ans;
	// 计算入度
    vector<int> indeg(numCourses);
    for (auto p : prerequisites) ++indeg[p[0]];
	// 建图
    vector<vector<int>> g(numCourses);
    for (auto p : prerequisites) g[p[1]].push_back(p[0]);
	// 入度 = 0 的点进队
    queue<int> q;
    for(int i = 0; i < numCourses; ++i) {
        if (indeg[i] == 0) q.push(i);
    }
	// 遍历邻接点，入度 -1，如果入度 =0，入队
    while (q.size()) {
        auto now = q.front(); q.pop();
        ans.push_back(now); // 记录答案
        for (auto nxt : g[now]) {
            if (--indeg[nxt]== 0) q.push(nxt);
        }
    }

    if (ans.size() != numCourses) return {}; // 如果小于总点数，说明有环，无法拓扑排序
    return ans;
}

bool topoSort_bfs() {
  for (int i = 1; i <= n; ++i)
    if (indeg[i] == 0) q.push(i);

  vector<int> ans;

  while (q.size()) {
    auto u = q.front(); q.pop();
    ans.push_back(u);
    for (auto v : g[u]) {
      if (--indeg[v] == 0) {
        q.push(v);
      }
    }
  }

  if (ans.size() == n) {
    for (int i = 0; i < ans.size(); ++i) {
      cout << ans[i] << " ";
    }
    return true;
  } else {
    cout << "不能拓扑排序";
    return false;
  }
}

DFS拓扑排序

class Solution {
public:
    vector<int> ans;
    vector<vector<int>> g;
    vector<int> vis;
    vector<int> findOrder(int n, vector<vector<int>>& prerequisites) {
        g = vector<vector<int>>(n);
        for (auto p : prerequisites) g[p[1]].push_back(p[0]);

        vis = vector<int>(n);
        for (int i = 0; i < n; ++i) {
            if (vis[i] == 0) {
                if (dfs(i) == false) return {};
            }
        }

        reverse(ans.begin(), ans.end());

        return ans;
    }

    bool dfs(int u) {
        vis[u] = 1;
        for (auto v : g[u]) {
            if (vis[v] == 0) {
                if (dfs(v) == false) return false;
            }
            if (vis[v] == 1) return false;
        }
        vis[u] = 2;
        ans.push_back(u);
        return true;
    }
};

enum statu { unvisited = 0, visiting = 1, visited = 2 };
statu st[N];
int stk[N], tt;
//单趟dfs拓扑排序
bool topodfs(int u) {
  st[u] = 1;  //正在遍历中
  for (int i = h[u]; ~i; i = ne[i]) {
    int j = e[i];
    if (st[j] == 0) {  //没有遍历过
      if (topodfs(j) == false) {
        return false;
      }
    } else if (st[j] == 1) {  //正在遍历中
      return false;
    }
  }
  st[u] = 2;      //已经遍历完
  stk[++tt] = u;  //入栈存储
  return true;
}

//判断整个图能否拓扑排序
bool topoSort() {
  for (int i = 1; i <= n; ++i) {
    if (st[i] == 0) {
      if (topodfs(i) == false) {
        cout << "不能拓扑排序" << endl;
        return false;
      }
    }
  }
  return true;
}

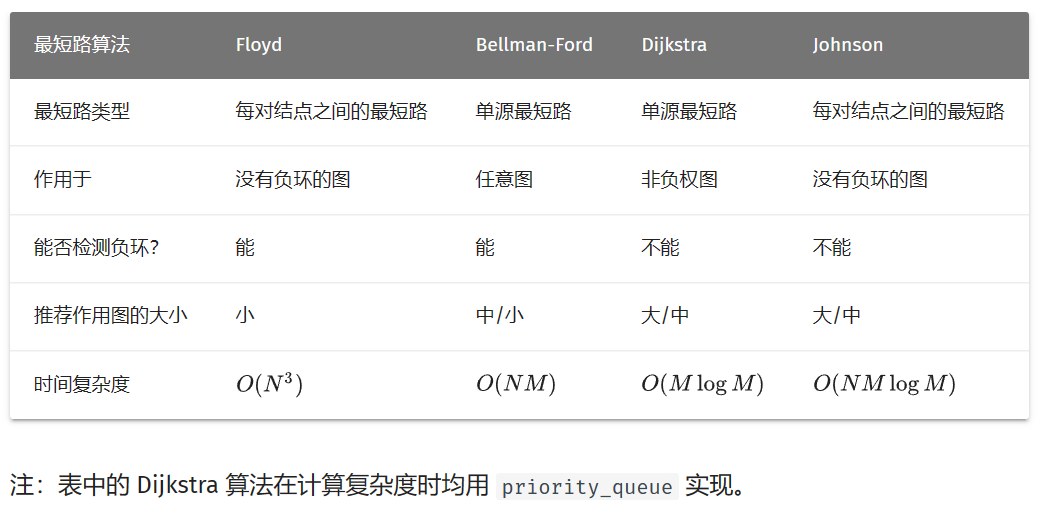
单源最短路

朴素Dijkstra算法

$O(V^2)$ $O(n^2)$

稠密图 $E\approx V^2$ 用邻接矩阵存图

集合S={当前已经确定最短距离的点}
更确切的含义：某个点是否已经更新过q
dist[1]=0,dist[其他点]=+∞
for i:1~n (循环n次)
	t<-不在S中(没有确定最短距离)的离1号最近的点
    s<-t，t就是已经确定最短距离的点了
    用t更新其他点的距离

void init() {
  memset(g, 0x3f, sizeof(g));
  memset(dist, 0x3f, sizeof(dist));
}
void add(int a, int b, int w) { g[a][b] = min(g[a][b], w); }
int dijkstra(int u) {
  dist[u] = 0;
  for (int i = 1; i < n; ++i) {
    int t = 0;
    for (int j = 1; j <= n; ++j) {
      if (st[j] == false && (t == 0 || dist[j] < dist[t])) {  //注意&&后要有括号
        t = j;
      }
    }
    st[t] = true;
    if (t == n) break;
    for (int j = 1; j <= n; ++j) {
      dist[j] = min(dist[j], dist[t] + g[t][j]);
    }
  }
  if (dist[n] == 0x3f3f3f3f) return -1;
  return dist[n];
}

堆优化版的Dijkstra算法

$O(ElogV)$ $O(mlogn)$
稀疏图 $E\approx V$ 用邻接表存图

堆实现方式：

手写堆

STL优先队列（可能有冗余）

一号点的距离初始化为零，其他点初始化成无穷大。
将一号点放入堆中。
不断循环，直到堆空。每一次循环中执行的操作为：
    弹出堆顶（与朴素版diijkstra找到S外距离最短的点相同，并标记该点）。
    用该点更新临界点的距离，若更新成功就加入到堆中。

int heapDijkstra(int u) {
  priority_queue<PII, vector<PII>, greater<PII>> heap;
  dist[u] = 0;
  heap.push({0, u});
  while (heap.size()) {
    auto t = heap.top();
    heap.pop();
    int v = t.second;
    if (st[v] == false) {
      if (v == n) break;
      st[v] = true;
      for (int i = h[v]; ~i; i = ne[i]) {
        int j = e[i], weight = w[i];
        if (dist[j] > dist[v] + weight) {
          dist[j] = dist[v] + weight;
          heap.push({dist[j], j});
        }
      }
    }
  }
  if (dist[n] == 0x3f3f3f3f) return -1;
  return dist[n];
}

Bellman-Ford

$O(VE)$ $O(mn)$
如果存在负权环路，最短路可能不存在
若最短路不存在时，只能用来判断是否存在负环
如果第n次操作仍可以更新，则存在负环
需要注意的是，以S点为源点跑 Bellman-Ford 算法时，如果没有给出存在负环的结果，只能说明从S点出发不能抵达一个负环，而不能说明图上不存在负环。因此如果需要判断整个图上是否存在负环，最严谨的做法是建立一个超级源点，向图上每个节点连一条权值为 0 的边，然后以超级源点为起点执行 Bellman-Ford 算法。

dist[1]=0,dist[其他点]=+∞
for n 次 (迭代k次涵义：从1号点经过不超过k条边的最短距离)
for 所有边 a->b w
	dist[b]=min(dist[b],dist[a]+w) 松弛操作

struct Edge {
  int a, b, w;
} edge[M];
void add(i, a, b, c) { edge[i] = {a, b, c}; }
bool bellmanford(int u, int k) {  //求出从u号点到n号点的最多经过k条边的最短距离
  memset(dist, 0x3f, sizeof dist);
  dist[u] = 0;
  for (int i = 0; i < k; ++i) {
    memcpy(backup, dist, sizeof dist);  //备份！！！
    for (int j = 0; j < m; ++j) {
      auto e = edge[j];
      dist[e.b] = min(dist[e.b], backup[e.a] + e.w);
    }
  }
  if (dist[n] > 0x3f3f3f3f / 2) return false;  //用0x3f3f3f3f/2仍是∞
  return true;
}

SPFA （Bellman-Ford队列优化版本）

一般 $O(E)$ $O(m)$ 这时候可以代替堆优化Dijkstra
最坏 $O(VE)$ $O(mn)$
图中不可以含有负权环路

Shortest Path Faster Algorithm

优化思路，当dist[a]变小时才需要更新dist[b]
借助队列来实现,队列存储更新过变小的点。(队列元素不要重复存储，入队出队时更新维护状态变量)

dist[x]表示1->x的最短距离
cnt[x]表示最短路径上的边数
cnt[x]>=n,表示至少经过了n条边，则至少经过了n+1个点，故肯定有负权环路

bool spfa(int u) {
  memset(dist, 0x3f, sizeof dist);
  queue<int> q;  //目的只是记录一下当前发生过更新的点，且不重复
  dist[u] = 0;
  q.push(u);
  st[u] = true;  //节点u在队列里面了
  while (q.size()) {
    auto v = q.front();
    q.pop();
    st[v] = false;  //出队，更新状态
    for (int i = h[v]; ~i; i = ne[i]) {
      int j = e[i], weight = w[i];
      if (dist[j] > dist[v] + weight) {
        dist[j] = dist[v] + weight;
        if (st[j] == false) {  //只有当前节点j不在队列里面才会入队
          q.push(j);           //入队
          st[j] = true;        //更新状态
        }
      }
    }
  }
  if (dist[n] == 0x3f3f3f3f) return false;
  return true;
}

bool spfaNegaCycle() {
  queue<int> q;
  for (int i = 1; i <= n; ++i) {
    q.push(i);
    st[i] = true;
  }
  while (q.size()) {
    auto v = q.front();
    q.pop();
    st[v] = false;
    for (int i = h[v]; ~i; i = ne[i]) {
      int j = e[i], weight = w[i];
      if (dist[j] > dist[v] + weight) {
        dist[j] = dist[v] + weight;
        cnt[j] = cnt[v] + 1;
        if (cnt[j] >= n) return true;
        if (st[j] == false) {
          q.push(j);
          st[j] = true;
        }
      }
    }
  }
  return false;
}

多源最短路

Floyd算法

$O(V^3)$ $O(n^3)$
邻接矩阵存图，dist[N][N]，既可以存图，也可以当点i，j距离

可以处理负权图，但不能有负权环路

d[k,i,j]表示i->1~k->j,从点i只经过1~k这些中间点到达j的最短距离
d[k,i,j]=d[k-1,i,k]+d[k-1,k,j]
d[i,j]=d[i,k]+d[k,j]
for(k=1;k<=n;++k){
	for(int i=1;i<=n;++i){
		for(int j=1;j<=n;++j){
			d[i,j]=min(d[i,j],d[i,k]+d[k,j]);
		}
	}
}
d[i,j]表示i->j的最短路长度

void init() {
  memset(dist, 0x3f, sizeof dist);
  for (int i = 1; i < N; ++i) {
    dist[i][i] = 0;  //删除自环，题目保证没有负权回路，数据中dist[a][b]>=0;
  }
}
void add(int a, int b, int c) { dist[a][b] = min(dist[a][b], c); }
void floyd() {
  for (int k = 1; k <= n; ++k) {
    for (int i = 1; i <= n; ++i) {
      for (int j = 1; j <= n; ++j) {
        dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j]);
      }
    }
  }
}

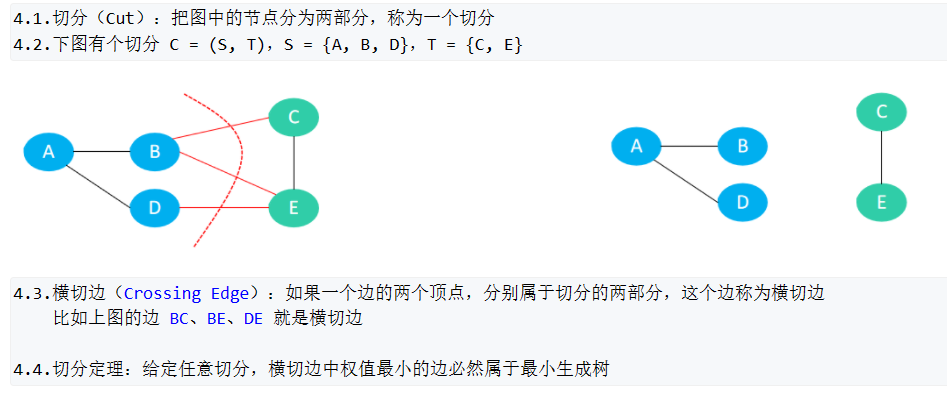
最小生成树

B站优质讲解

普利姆算法Prim

如果图的每一条边的权值都互不相同，那么最小生成树将只有一个，否则可能会有多个最小生成树
Prim算法是基于切分定理

朴素版Prim

稠密图适用
$O(n^2)$

dist[i]<-∞
集合S={当前已经在连通块中的所有点}
for(i=0;i<n;++i)
	v<-找到集合外距离最近的点
	用v更新其它点到_集合_的距离(Dijkstra算法为到源点距离)
	st[v]=true，将点v加入到集合

bool prim() {
  memset(dist, 0x3f, sizeof dist);
  for (int i = 0; i < n; ++i) {
    int t = -1;
    for (int j = 1; j <= n; ++j) {
      if (st[j] == false && (t == -1 || dist[t] > dist[j])) {
        t = j;
      }
    }
    //有点不连通的时候，不存在最小生成树
    if (i && dist[t] == INF) return false;
    // dist[t]是最小的横切边，必然属于最小生成树
    if (i) res += dist[t];
    st[t] = true;
    for (int j = 1; j <= n; ++j) {
      dist[j] = min(dist[j], g[t][j]);
    }
  }
  return true;
}

堆优化版Prim

不常用
$O(mlogn)$

克鲁斯卡尔算法Kruskal

稀疏图适用
$O(mlogm)$

将所有边按权重从小到大排序 
枚举每条边a->b,权重w
	if a,b不连通
		将这条边加入集合

struct Edge {
  int a, b, w;
  bool operator<(const Edge &e) const { return w < e.w; }
} edge[M];
bool kruskal() {
  sort(edge, edge + idx);                 //边排序
  for (int i = 1; i <= n; ++i) p[i] = i;  //初始化并查集
  for (int i = 0; i < idx; ++i) {         //枚举边
    int a = edge[i].a, b = edge[i].b, w = edge[i].w;
    int pa = findroot(a), pb = findroot(b);
    if (pa != pb) {  //不连通
      p[pa] = pb;    //合并成连通块
      res += w;
      ++cnt;                    //记录连通块中边的数量
      if (cnt == n - 1) break;  //可以提前结束
    }
  }
  if (cnt < n - 1) return false;
  return true;
}

二分图

二分图当且仅当图中不含有奇数环

染色法

$O(n+m)$

DFS版染色法

class Solution {
public:
    vector<int> color;
    bool isBipartite(vector<vector<int>>& graph) {
        int n = graph.size();
        color.resize(n);
        for (int i = 0; i < n; ++i) {
            if (color[i] == 0) { // 还没有被染色
                if (dfs(graph, i, 1) == false) return false; // 染色失败
            }
        }
        return true;
    }

    bool dfs(vector<vector<int>>& graph, int u, int c) {
        color[u] = c; // 染色
        for (auto v : graph[u]) { // 遍历所有邻接点
            if (color[v] == 0) // 如果邻接点没有被染色
                if (dfs(graph, v, 3 - c) == false) return false; // 对邻接点染色，若失败则返回
            if (color[v] == c) return false; // 如果邻接点颜色和当前颜色相同，染色失败
        }
        return true;
    }
};

bool dfs(int u, int c) {
  color[u] = c;
  for (int i = h[u]; ~i; i = ne[i]) {
    int j = e[i];
    if (color[j] == 0) {
      if (dfs(j, 3 - c) == false) return false;
    } 
    if (color[j] == c) return false;
  }
  return true;
}
bool isBipartite() {
  for (int i = 1; i <= n; ++i) {
    if (color[i] == 0) {
      if (dfs(i, 1) == false) return false;
    }
  }
  return true;
}

BFS版染色法

bool bfs(int u) {
  queue<int> q;
  color[u] = 1;
  q.push(u);
  while (q.size()) {
    auto t = q.front();
    q.pop();
    for (int i = h[t]; ~i; i = ne[i]) {
      int j = e[i];
      if (color[j] == 0) {
        color[j] = 3 - color[t];
        q.push(j);
      } 
      if (color[j] == color[t]) return false;
    }
  }
  return true;
}
bool isBipartite() {
  for (int i = 1; i <= n; ++i) {
    if (color[i] == 0) {
      if (bfs(i) == false) {
        return false;
      }
    }
  }
  return true;
}

匈牙利算法

最坏 $O(mn)$ ，实际运行时间远小于 $O(mn)$

bool findmatch(int u) {
  for (int i = h[u]; ~i; i = ne[i]) {
    int j = e[i];
    if (st[j] == false) {
      st[j] = true;
      if (match[j] == 0 || findmatch(match[j])) {
        match[j] = u;
        return true;
      }
    }
  }
  return false;
}
int Maxmatch() {
  int cnt = 0;
  for (int i = 1; i <= n1; ++i) {
    memset(st, 0, sizeof st);
    if (findmatch(i)) {
      ++cnt;
    }
  }
  return cnt;
}

数学知识

位运算

按位异或

归零率 $a\oplus a=0$
恒等率 $a\oplus0=a$
$a\oplus1=\sim a$

质数（素数）Prime

定义：质数又称素数。一个大于1的自然数，除了1和它自身外，不能被其他自然数整除的数叫做质数；否则称为合数（规定1既不是质数也不是合数）

质数的判定——试除法

“d|n"表示d能整除n
一个合数的约数总是成对出现的，若d|n，则(n/d)|n，因此我们判读一个数是否为质数的时候，只需要判断较小的那个数能否整除n就行了，即只需要枚举到d<=(n/d)，即d*d<=n，d<=sqrt(n)就行了
1
2
3
4
5
6
7
8
9
10
bool isPrime(int x){
if(x<2)return false;
int sqrtX=sqrt(x);
for(int i=2;i<=sqrtX;++i){
if(x%i==0){
return false;
}
}
return true;
}

分解质因数——试除法

算数基本定理：任何一个大于1的自然数N，如果N不为质数，那么N可以唯一分解成有限个质数的乘积。

$N=P_1^{a_1}P_2^{a_2}P_3^{a_3}...P_n^{a_n}$ ，这里 $P_1<P_2<P_3<...<P_n$ 均为质数，其中指数 $a_i$ 是正整数。

这样的分解称为N的标准分解式。

一个大于1的正整数 $N$ ，如果它的标准分解式为： $N=P_1^{a_1}P_2^{a_2}...P_n^{a_n}$ ，

正因数个数为：

$\sigma_0(N)=(1+a_1)(1+a_2)(1+a_3)...(1+a_n)$

正因数之和为： $\sigma_1(N)=(1+p_1+p_1^2+...+p_1^{a_1})(1+p_2+p_2^2+...+p_2^{a_2})...(1+p_n+p_n^2+...+p_n^{a_n})$

当 $\sigma_1=2N$ 时就称N为完全数。

整数a,b的最大公因子 $(a,b)$ 和最小公倍数 $[a,b]$ ，则 $ab=(a,b)\times[a,b]$

unordered_map<int,int> prime;
void divide(int n){
    for(int i=2;i<=n/i;++i){
        while(n%i==0){
            ++prime[i];
            n/=i;
        }
    }
    if(n>1) ++prime[n];
}

一个合数分解而成的质因数最多只包含一个大于 $sqrt(n)$ 的质因数
当枚举到一个数 $i$ 的时候， $n$ 的因子里面已经不包含 $[2,i-1]$ 里面的数（已经被除干净了）。
如果 $n\%i==0$ ，则 $i$ 的因子里面也已经不包含 $[2,i-1]$ 里面的数，因此每次枚举的数都是质数
两个没有共同质因子的正整数称为互质。因为 $1$ 没有质因子，故 $1$ 与任何正整数（包括 $1$ 本身）都是互质。
只有一个质因子的正整数也即质数。

筛质数（朴素筛法）

步骤：把 $[2,n-1]$ 中所有的数的倍数都标记上，最后没有被标记的数就是质数。
原理：假定有一个数 $p$ 未被 $[2,p-1]$ 中的数标记过，那么说明，不存在 $[2,p-1]$ 中的任何一个数的倍数时 $p$ ，也就是说 $[2,p-1]$ 中不存在 $p$ 的约数，因此，根据质数的定义可知： $p$ 是质数。

$O(nlogn)$

bool notprime[N];
int prime[N],cnt;
int getPrime(int n){
    for(int i=2;i<=n;++i){
        if(notprime[i]==false){
            prime[cnt++]=i;
        }
        for(int j=2*i;j<=n;j+=i){
            notprime[j]=true;
        }
    }
}

埃式筛法（稍加优化版的朴素筛法）

质数定理： $1\sim n$ 中有 $n\over \ln n$ 个质数。
步骤：在朴素筛法的过程中只用质数项去筛
$O(nlog(logn))$

bool composite[N];
int prime[N],cnt;
void getPrime(int n){
    for(int i=2;i<=n;++i){
        if(composite[i]==false){
            prime[cnt++]=i;
            if(i<=n/i){
                for(int j=i*i;j<=n;j+=i){
                    composite[j]=true;
                }
                //因为从2到i-1的倍数我们之前筛过了
                //这里直接从i倍开始，提高了运行速度
            }
        }
    }
}

线性筛法

若 $n\approx10^6$ ，线性筛和埃式筛的时间效率差不多，若 $n\approx10^7$ ，线性筛比埃式筛要快一倍
核心： $1\sim n$ 内的每一个合数 $p$ 只被其最小质因子筛掉
原理： $1\sim n$ 之内的任何一个合数一定会被筛掉，而且筛的时候只用最小质因子来筛，然后每一个数都只有一个最小质因子，因此每个数都只会被筛一次，因此线性筛法是线性的
当 i%primes[j]!=0时,说明此时遍历到的 primes[j]不是 i的质因子，那么 primes[j]一定小于 i的最小质因子，所以 primes[j]*i的最小质因子就是 primes[j];
当有 i%primes[j]==0时,说明 i的最小质因子是 primes[j],因此 primes[j]*i的最小质因子也就应该是
prime[j]。

之后接着用 st[primes[j+1]*i]=true去筛合数时，就不是用最小质因子去更新了,因为 i有最小质因子 primes[j],此时的 primes[j+1]不是 primes[j+1]*i的最小质因子，此时就应该退出循环，避免之后重复进行筛选。
$O(n)$

bool composite[N];
int prime[N],cnt;
void getPrime(int n){
    for(int i=2;i<=n;++i){
        if(composite[i]==false){
            prime[cnt++]=i;
        }
        for(int j=0;prime[j]<=n/i;++j){
            composite[prime[j]*i]=true;
            if(i%prime[j]==0)break;
        }
    }
}

约数（因数）Divisor（Factor）

定义：若整数 $n$ 除以整数 $d$ 的余数为0，即 $d$ 能整除 $n$ ，则称 $d$ 是 $n$ 的约数， $n$ 是 $d$ 的倍数，记为 $d|n$ 。

在算数基本定理中，若正整数 $N$ 被唯一分解为 $N=p_{1}^{c_{1}} p_{2}^{c_{2}} \cdots p_{m}^{c_{m}}$ ，其中 $c_i$ 都是正整数， $p_i$ 都是质数，且满足 $p_{1}<p_{2}<\cdots<p_{m}$ ，则 $N$ 的正约数集合可写作：

$\left\{p_{1}^{b_{1}} p_{2}^{b_{2}} \cdots p_{m}^{b_{m}}\right\}, \text { 其中 } 0 \leq b_{i} \leq c_{i}$

$N$ 的正约数个数为：

$\left(c_{1}+1\right) *\left(c_{2}+1\right) * \cdots *\left(c_{m}+1\right)=\prod_{i=1}^{m}\left(c_{i}+1\right)$

$N$ 的所有正约数的和为：

$\left(1+p_{1}+p_{1}^{2}+\cdots+p_{1}^{c_{1}}\right) * \cdots *\left(1+p_{m}+p_{m}^{2}+\cdots+p_{m}^{c_{m}}\right)=\prod_{i=1}^{m}\left(\sum_{j=0}^{c_{i}}\left(p_{i}\right)^{j}\right)$

求 $N$ 的正约数集合——试除法

若 $d \geq \sqrt{N}$ 是 $N$ 的约数，则 $N / d \leq \sqrt{N}$ 也是 $N$ 的约数。

换言之，约数总是成对出现的（除了对于完全平方数， $\sqrt{N}$ 会单独出现）。
因此，只需要扫描 $d=1 \sim \sqrt{N}$ ，尝试 $d$ 能否整除 $N$ ，若能整除，则 $N/d$ 也是 $N$ 的约数。
推论：一个整数 $N$ 的约数个数上界为 $2\sqrt{N}$ 。
$O(\sqrt{N})$

vector<int> getFactor(int n){
    vector<int> factor;
    for(int i=1;i<=n/i;++i){
        if(n%i==0){
            factor.push_back(i);
            if(i!=n/i)factor.push_back(n/i);
        }
    }
    sort(factor.begin(),factor.end());
    return factor;
}

求 $N$ 的约数个数

unordered_map<int,int> prime;
void getPrimeFactor(int n){
    for(int i=2;i<=n/i;++i){
        while(n%i==0){
            ++prime[i];
            n/=i;
        }
    }
    if(n>1) ++prime[n];
}
long long countFactor=1;
for(auto it:prime){
    countFactor=countFactor*(it.second+1)%mod;
}

求 $N$ 的约数之和

unordered_map<int,int> prime;
void getPrimeFactor(int n){
    for(int i=2;i<=n/i;++i){
        while(n%i==0){
            ++prime[i];
            n/=i;
        }
    }
    if(n>1) ++prime[n];
}
for(auto it:prime){
    long long p=it.first, index=it.second;
    long long sum=1;
    while(index--){
        sum=(sum*p+1)%mod;
    }
    res=res*sum%mod;
}

最大公约数

欧几里得算法（辗转相除法）
$gcd(a,b)=gcd(b,a\mod b)$
$O(logn)$

1
2
3

int gcd(int a,int b){
    return b?gcd(b,a%b):a;
}

int gcd(int a,int b){
    while(b){
        int r=a%b;
        a=b;
        b=r;
    }
    return a;
}

欧拉函数

定义和性质

互质： $\forall a, b \in \mathbb{N} \text {, 若 } \operatorname{gcd}(a, b)=1, \text { 则称 } a, b \text { 互质 }$

欧拉函数： $1 \sim N \text { 中与 } N \text { 互质的数的个数被称为欧拉函数, 记为 } \varphi(N)$

求欧拉函数

$O(\sqrt{n})$

int phi(int n){
    int cnt=n;
    for(int i=2;i<=n/i;++i){
        if(n%i==0){
            cnt=cnt/i*(i-1); //先除后乘防溢出
            while(n%i==0) n/=i;//注意要用while把质数i除干净
        }
    }
    if(n>1) cnt=cnt/n*(n-1);
    return cnt;
}

筛法求欧拉函数

$O(n)$

int prime[N],cnt;
bool iscomposite[N];
int e[N];
void getEulers(int n){
    e[1]=1;//注意要写上！！！
    for(int i=2;i<=n;++i){
        if(iscomposite[i]==false){
            prime[cnt++]=i;
            e[i]=i-1;
        }
        for(int j=0;prime[j]<=n/i;++j){
            int p=prime[j];
            iscomposite[p*i]=true;
            if(i%p==0){	//p是i的最小质因子
                e[p*i]=p*e[i];
                break;
            }else{	//p与i互质
                e[p*i]=e[p]*e[i];
            } 
        }
    }
}

欧拉定理

若 $\operatorname{gcd}(a, m)=1$ ，则 $a^{\varphi(m)} \equiv 1\ (\bmod m)$

扩展欧拉定理

$a^{b} \equiv \begin{cases}a^{b\;\bmod\; \varphi(m)}, & \operatorname{gcd}(a, m)=1, \\ a^{b}, & \operatorname{gcd}(a, m) \neq 1, b<\varphi(m), \quad(\bmod m) \\ a^{b\;\bmod \;\varphi(m)+\varphi(m)}, & \operatorname{gcd}(a, m) \neq 1, b \geq \varphi(m) .\end{cases}$

费马小定理

$p$ 为质数
若 $\operatorname{gcd}(a, p)=1$ ，则 $a^{p-1} \equiv 1\ (\bmod p)$
$\forall a \in \mathbb{Z}$ ，有 $a^{p} \equiv a \ (\bmod p)$

$^{b} \equiv \begin{cases}a^{b\;\bmod\;\varphi(p)}, & \operatorname{gcd}(a, p)=1, \\ a^{b}, & \operatorname{gcd}(a, p) \neq 1, b<\varphi(p) \quad(\bmod p) \\ a^{b\;\bmod \;\varphi(p)+\varphi(p)}, & \operatorname{gcd}(a, p) \neq 1, b \geq \varphi(p) \end{cases} \quad\varphi(p)=p-1$

快速幂

$\Theta(\log n)$

using LL=long long ;
LL binpow(LL a,LL n,LL p){
    a%=p;
    LL res=1;
    while(n){
        if(n&1)res=res*a%p;
        a=a*a%p;
        n>>=1;
    }
    return res;
}

裴蜀定理

设 $a,b$ 是不全为零的整数，则存在整数 $x,y$ ，使得 $ax+by=\gcd (a,b)$

扩展欧几里得算法 EXGCD

算法原理

求解 $ax+by=\gcd (a,b)$

由欧几里得定理可知： $\gcd (a,b)=\gcd(b,a\mod b)$

设 $ax_1+by_1=\gcd (a,b) =\gcd (b,a\mod b)=bx_2+(a\mod b)y_2$

$a \mod b=a-(\lfloor \frac ab\rfloor \times b) \Rightarrow$

$ax_1+by_1=bx_2+(a-\lfloor \frac ab\rfloor \times b)y_2=ay_2+b(x_2-\lfloor \frac ab \rfloor y_2)$

故 $x_1=y_2\ ,\ y_1=x_2-\lfloor \frac ab \rfloor y_2$

递归写法

int exgcd(int a,int b,int &x1,int &y1){
    if(b==0){
        x1=1,y1=0;
        return a;
    }
    int x2,y2;
    int d=exgcd(b,a%b,x2,y2);
    x1=y2,y1=x2-(a/b)*y2;
    return d;
}

矩阵解释

$\gcd(a,b)=\gcd(b,a\bmod b)$ 使用矩阵表示为

$\begin{bmatrix}b\\a\bmod b\end{bmatrix}= \begin{bmatrix}0&1\\1&-\lfloor \frac ab \rfloor\end{bmatrix} \begin{bmatrix}a\\b\end{bmatrix}$

定义变换：

$\begin{bmatrix}a\\b\end{bmatrix} \mapsto \begin{bmatrix}0&1\\1&-\lfloor \frac ab \rfloor\end{bmatrix} \begin{bmatrix}a\\b\end{bmatrix} =\begin{bmatrix}b\\a\bmod b\end{bmatrix}$

欧几里得算法即不停应用该变换

$\left( \begin{bmatrix}0&1\\1&-\lfloor \frac ab \rfloor\end{bmatrix} \cdots \begin{bmatrix}0&1\\1&-\lfloor \frac ab \rfloor\end{bmatrix} \right) \begin{bmatrix}a\\b\end{bmatrix} = \begin{bmatrix}\gcd(a,b)\\0\end{bmatrix}$

$\begin{bmatrix}x_1&x_2\\x_3&x_4\end{bmatrix} \begin{bmatrix}a\\b\end{bmatrix} = \begin{bmatrix}\gcd(a,b)\\0\end{bmatrix}$

则有 $ax_1+bx_2=\gcd(a,b)$

初始化：

$\begin{bmatrix}x_1&x_2\\x_3&x_4\end{bmatrix} = \begin{bmatrix}1&0\\0&1\end{bmatrix}$

迭代：

$\begin{bmatrix}a\\b\end{bmatrix} \mapsto \begin{bmatrix}0&1\\1&-\lfloor \frac ab \rfloor\end{bmatrix} \begin{bmatrix}a\\b\end{bmatrix} =\begin{bmatrix}b\\a\bmod b\end{bmatrix}$

$\begin{bmatrix}x_1&x_2\\x_3&x_4\end{bmatrix} \mapsto \begin{bmatrix}0&1\\1&-\lfloor \frac ab \rfloor\end{bmatrix} \begin{bmatrix}x_1&x_2\\x_3&x_4\end{bmatrix} =\begin{bmatrix}x_3&x_4\\x_1-\lfloor \frac ab \rfloor x_3&x_2-\lfloor \frac ab \rfloor x_4\end{bmatrix}$

int exgcd(int a, int b, int &x, int &y) {
    int x1=1,x2=0,x3=0,x4=1;
    while(b){
        int c=a/b,tx1=x1,tx2=x2;
        x1=x3,x2=x4,x3=tx1-c*x3,x4=tx2-c*x4;
        int r=a%b;
        a=b,b=r;
    }
    x=x1,y=x2;
    return a;
}

int exgcd(int a, int b, int &x, int &y) {
    int x1=1,x2=0,x3=0,x4=1;
    while(b){
        int c=a/b;
        tie(x1,x2,x3,x4,a,b)=make_tuple(x3,x4,x1-c*x3,x2-c*x4,b,a%b);
    }
    x=x1,y=x2;
    return a;
}

求解 $ax+by=c$

$ax+by=c$ 有解当且仅当 $\gcd(a,b)|c$

先求得 $ax_0+by_0=\gcd (a,b)=d$ 的解 $x_0,y_0$

则有特解 $x'=x_0\frac cd\;,y'=y_0\frac cd$

故通解为 $x=x_0\frac cd +k\frac bd,y=y_0\frac cd -k\frac ad$

1
2
3

int d=exgcd(a,b,x,y);
if(c%d==0) cout<<x*1LL*c/d<<endl;
else cout<<"impossible"<<endl;

求线性同余方程 $ax\equiv c\;(\bmod\;b)$

$ax\equiv c\;(\bmod\;b) \Leftrightarrow\; ax=(-y)\times b+c\;\Leftrightarrow\; ax+by=c$
有解当且仅当 $\gcd(a,b)|c$ ，特别的，当 $c=1$ ， $a$ 与 $b$ 互质时，则所求的 $x$ 为 $a$ 的逆元
1
2
3
int d=exgcd(a,b,x,y);
if(c%d==0) cout<<x*1LL*c/d<<endl;
else cout<<"impossible"<<endl;

逆元

如果一个线性同余方程 $ax\equiv 1\;(\bmod m)$ ，则 $x$ 称为 $a\bmod m$ 的逆元，记作 $a^{-1}$
$a$ 逆元存在的充要条件是 $a,m$ 互质， $\gcd(a,m)=1$
$aa^{-1}\equiv1\;(\bmod m)\;,\;bb^{-1}\equiv1\;(\bmod m)\Rightarrow aba^{-1}b^{-1} \equiv 1\;(\bmod m)\;,\;(ab)^{-1}=a^{-1}b^{-1}$

扩展欧几里得法求逆元

int exgcd(int a,int b,int &x,int &y){
    if(b==0){
        x=1,y=0;
        return a;
    }
    int d=exgcd(b,a%b,y,x);
    y-=a/b*x;
    return d;
}
int x,y;
int d=exgcd(a,m,x,y);
if(d==1) cout<<((LL)x%p+p)%p<<endl;
else cout<<"impossible";

快速幂法求逆元（模m必须为质数）

若 $m$ 为质数，则根据费马小定理有 $a^{m}\equiv a\;(\bmod m)$

因为 $ax\equiv 1\;(\bmod m)$ ，故 $a^2x\equiv a\equiv a^m\;(\bmod m)$

$a,m$ 互质，则有 $x=a^{-1}\equiv a^{m-2}\;(\bmod m)$

LL binpow(int a,int n,int p){
    a%=p;
    LL res=1;
    while(n){
        if(n&1)res=res*a%p;
        n>>=1;
        a=a*1LL*a%p;
    }
    return res;
}
//这里模m必须为质数
if(a%m) cout<<binpow(a,m-2,m)%<<endl;
else cout<<"impossible"<<endl;

中国剩余定理CRT

求解如下形式的一元线性同余方程组：

$\begin{cases} x\equiv a_1\;(\bmod m_1)\\x\equiv a_2\;(\bmod m_2)\\ \;\;\;\;\;\;\;\;\;\;\;\vdots \\x\equiv a_k\;(\bmod m_k)\end{cases}$

其中 $n_1,n_2,\cdots,n_k$ 两两互质

算法流程:

计算所有模数的积 $n=n_1\times n_2\times n_3\times\cdots\times n_k$

对于第 $i$ 个方程：

计算 $m_i=\frac n{n_i}$

计算 $m_i$ 在模 $n_i$ 意义下的逆元 $m_i^{-1}$

计算 $c_i=m_im_i^{-1}$ (不要对 $n_i$ 取模)

方程组的唯一解为： $x=\sum_{i=1}^{k}a_ic_i\;(\bmod n)$

通解为： $x+km\;(k\in\Z)$

模数不互质的情况

两个方程

$\begin{cases} x\equiv a_1\;(\bmod m_1)\\x\equiv a_2\;(\bmod m_2)\end{cases}$

转为不定方程 $x=m_1k_1+a_1=m_2k_2+a_2$ ，其中 $k_1,k_2$ 是整数

则有 $m_1k_1-m_2k_2=a_2-a_1$

由裴蜀定理，若 $\gcd(m_1,m_2)\nmid a_2-a_1$ ，不定方程无解。

若 $\gcd(m_1,m_2)\mid a_2-a_1$ ，可由扩展欧几里得算法求出一组可行解 $(k_1,k_2)$

则原方程解为 $x\equiv b\;(\bmod M)$ ，其中 $b=m_1k_1+a_1\;,\;M=\text{lcm} (m_1,m_2)$
- 欧几里得算法求解 $m_1k_{01}+m_2k_{02}=a_2-a_1$
- $d=\text{exgcd}(m_1,m_2,k_{01},k_{02})$ 得特解 $k_1'=\frac {a_2-a_1}{d} k_{01},k_2'=\frac {a_2-a_1}{d} k_{02}$
- 则有通解
  
  $k_1=k'+k\frac {m_2}{d}=\frac {a_2-a_1}{d} k_{01}+k\frac{m_2}{d}$
  
  $k_2=-(k_2'-k\frac{m_1}{d})=-\frac {a_2-a_1}{d} k_{02}+k\frac{m_1}{d}$
  
  其中 $k\in \Z$
- 为了防止计算过程中出现溢出，需要在通解 $k_1$ 中选出一个尽可能小的特解 $k_1^*$ 替代 $k_{01}$ ，此处取为最小正整数特解。
  
  C++中求 $x=x_0+kd$ 的最小正整数解：
  
  $(x\%d+d)\%d$
  
  $k_1^*=(k_1\% \frac {m_2}{d}+\frac{m_2}{d})+\frac{m_2}{d}$
  
  $k_1=k_1^*+k\frac {m_2}{d}$
- 将求出的 $k_1^{*}$ 代入原不定方程得：
  begin{align*}x&=m_{1} k_{1} + a_{1} \\&= m_{1} k_{1}^{*} + m_{1} k \frac{m_{2}}{d} + a_{1} \\&= k \frac{m_{1} m_{2}}{d} + (a_{1} + m_{1} k_{1}^{*})\end{align*}
  记 $a=a_1+m_1k_1^*\;,\;m=\frac{m_1m_2}{d}=\text{lcm}(m_1,m_2)$
  
  则原来的两个方程可以表示为：
  
  $x=km+a$ 即 $x\equiv a\;(\bmod m)$

多个方程

用上面的方法两两合并即可。

usign LL=long long;
int n; cin>>n;
LL a1,m1; cin>>m1>>a1;
bool flag=true;
while(--n){
    LL a2,m2; cin>>m2>>a2;
    LL k1,k2;
    LL d=exgcd(m1,m2,k1,k2);
    if((a2-a1)%d==0){
        k1*=(a2-a1)/d;
        LL mod=m2/d;
        k1=(k1%mod+mod)%mod;
        a1+=m1*k1;
        m1*=mod;
    }else{
        flag=false;
        break;
    }
}
if(flag) cout<<a1%m1<<endl;
else cout<<-1<<endl;

高斯消元

通过初等行变换把增广矩阵变为简化阶梯型矩阵

算法步骤：

找到当前列绝对值最大的一行
将该行与未确定阶梯型的顶行交换
对该行进行行变换使得非零首元素变为1
进行行变换使得下面所有行的当前列变成0
从下往上依次求解每个未知量

int gauss(){
    int r,c;
    // 枚举每一列
    for(r=0,c=0;c<n;++c){
        int t=r;
		// 1. 找出c这一列绝对值最大的数 所在的行
        for(int i=r;i<n;++i){// 这里i枚举的是行
            if(abs(a[i][c])>abs(a[t][c])){
                t=i;
            }
        }
        // 如果这一列上所有的数都是0的话 , 看下一列
        if(abs(a[t][c])<eps){
            continue;
        }
        // 2. 让第t行(首元素绝对值最大的那一行)与未固定的行(第r行)的第一行交换
        for(int i=c;i<=n;++i) swap(a[r][i],a[t][i]);
        // 3. 把这一行非零首元素变为1
        for(int i=n;i>=c;--i) a[r][i]/=a[r][c];
        // 4. 将下面所有行的第c列(当前枚举列)变为0
        for(int i=r+1;i<n;++i){
            if(abs(a[i][c])>eps){
                for(int j=n;j>=c;--j){
                    a[i][j]-=a[i][c]*a[r][j];
                }
            }
        }
        //该行已固定，处理下一行
        ++r;
    }
    // 通过r来观察方程解的数量
    if(r<n){
        for(int i=r;i<n;++i){
            if(abs(a[i][n])>eps) return 2;
        }
        return 1;
    }
    // 从下往上， 依次求出方程的解
    for(int i=n-1;i>=0;--i){
        for(int j=i+1;j<n;++j){
            a[i][n]-=a[j][n]*a[i][j];
        }
    }
    return 0;
}

组合数

$C_n^m=\frac {n!}{m!(n-m)!}$

$C_n^m=C_n^{n-m}$

$C_n^m=C_{n-1}^{m-1}+C_{n-1}^m$

$C_n^0+C_n^1+C_n^2+\cdots+C_n^n=2^n$

递推法 $O(n^2)$

$C_n^m=C_{n-1}^{m-1}+C_{n-1}^m$

void init(){
    for(int i=0;i<N;++i){
        for(int j=0;j<=i;++j){
            if(j==0){
                c[i][j]=1;
            }else{
                c[i][j]=(c[i-1][j-1]+c[i-1][j])%mod;
            }
        }
    }
}

预处理阶乘

用快速幂求逆元

$C_n^m=\frac {n!}{m!(n-m)!}=n!(m!)^{-1}(n-m)^{-1}$
预处理 $n!\;,\;(m!)^{-1}\;,\;(n-m)^{-1}$
$O(NlogN)$

int binpow(int a,int n,int p){
    long long res=1;
    while(n){
        if(n&1)res=res*a%mod;
        n>>=1;
        a=1LL*a*a%mod;
    }
    return res;
}
void factorial(){
    fact[0]=infact[0]=1;
    for(int i=1;i<N;++i){
        fact[i]=1LL*fact[i-1]*i%mod;
        infact[i]=1LL*infact[i-1]*binpow(i,mod-2,mod)%mod;
    }
}
int C(int n,int m){
    return 1LL*fact[n]*infact[m]%mod*infact[n-m]%mod;
}

Lucas 定理

$C_n^m \equiv C_{n/p}^{m/p}C_{n\;\bmod\;p}^{m\;\bmod\;p}\;(\bmod\;p)$
当问题规模很大，而模数是一个不大的质数的时候，就不能简单地通过递推求解来得到答案，需要用到 Lucas 定理， $p$ 一般在 $10^5$ 左右，模数 $p$ 必须为质数
$O(f(p)+g(n)\log n)$ 其中 $f(n)$ 为预处理组合数的复杂度， $g(n)$ 为单次求组合数的复杂度
$C_{n}^{m}=\frac{n!}{(n-m) ! m !}=\frac{n (n-1) (n-2) \cdots (n-m+1) (n-m) \cdots 1}{(n-m) (n-m-1) \cdots 1 \times m !}=\frac{n (n-1) (n-2) \cdots(n-m+1)}{m !}$

int binpow(int a,int n,int p){
    long long res=1;
    while(n){
        if(n&1)res=res*a%p;
        n>>=1;
        a=1LL*a*a%p;
    }
    return res;
}
int C(int a,int b,int p){
    if(a<b)return 0;
    long long res=1;
    for(int i=1,j=a;i<=b;++i,--j){
        res=res*j%p*binpow(i,p-2,p)%p;
    }
    return res; 
}
int Lucas(long long a,long long b,int p){
    if(a<p&&b<p) return C(a,b,p);
    return 1LL*C(a%p,b%p,p)*Lucas(a/p,b/p,p)%p;
}

卡特兰数

$H_0$	$H_1$	$H_2$	$H_3$	$H_4$	$H_5$	$H_6$
1	1	2	5	14	42	132

$H_n=\frac {4n-2}{n+1}H_{n-1}\;,\;H_0=1$

$H_n=C_{2n}^n-C_{2n}^{n-1}=\frac {C_{2n}^n}{n+1}=\frac{(2n)!}{n!n!}=\frac{(2n)(2n-1)\cdots(n+1)}{n!}$

int binpow(int a,int n,int p){
    long long res=1;
    while(n){
        if(n&1)res=res*a%mod;
        n>>=1;
        a=1LL*a*a%mod;
    }
    return res;
}
int catalan(int n){
    long long res=1;
    for(int i=n+1;i<=2*n;++i)res=res*i%mod;
    for(int i=1;i<=n;++i)res=res*binpow(i,mod-2,mod)%mod;
    res=res*binpow(n+1,mod-2,mod)%mod;  
    return res;
}

路径计数问题

非降路径是指只能向上或向右走的路径
从 $(0,0)$ 到 $(m,n)$ 的非降路径数等于 $m$ 个 $x$ 和 $n$ 个 $y$ 的排列数，即 $C_{m+n}^m$

$P(m,n)\rightarrow P(m+1,n-1)$

不穿过 $y=x$ 的路径条数： $C_{m+n}^{n}-C_{m+n}^{n-1}$ ， $m=n$ 时即卡特兰数 $H_n=C_{2n}^n-C_{2n}^{n-1}$

容斥原理

$\left|\bigcup_{i=1}^{n} S_{i}\right|=\sum_{m=1}^{n}(-1)^{m-1} \sum_{a_{i}<a_{i+1}}\left|\bigcap_{i=1}^{m} S_{a_{i}}\right|$

int res=0;
for(int i=1;i<(1<<m);++i){
    int t=1;
    int s=0;
    for(int j=0;j<m;++j){
        if(i>>j&1){
            if(1LL*t*p[j]>n){
                t=-1;
                break;
            }  
            ++s;
            t*=p[j];
        }
    }
    if(t!=-1){
        if(s&1)res+=n/t;
        else res-=n/t;
    }
}
cout<<res<<endl;

动态规划

背包DP

题意概要：有 $N$ 个物品和一个容量为 $V$ 的背包，每个物品有体积 $v_i$ 和价值 $w_i$ 两种属性，要求选若干物品放入背包使背包中物品的总价值最大且背包中物品的总体积不超过背包的体积

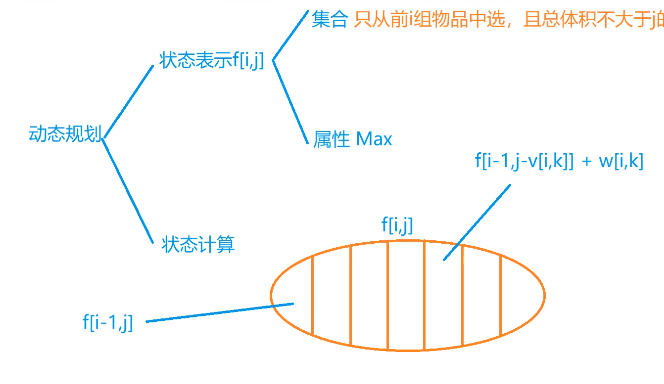
0-1背包

已知条件有第 $i$ 个物品的体积 $v_i$ ，价值 $w_i$ ，以及背包的总容量 $V$ 。设 DP 状态 $f_{i,j}$ 为在只能放前 $i$ 个物品的情况下，容量为 $j$ 的背包所能达到的最大总价值。

考虑转移：初始状态 $f_{0,j}=0$ ，假设当前已经处理好了前 $i-1$ 个物品的所有状态，那么对于第 $i$ 个物品：

选择不加入第 $i$ 个物品，背包的剩余容量不变，背包中物品的总价值也不变，此时背包的价值为 $f_{i,j}=f_{i-1,j}$
选择加入第 $i$ 个物品（若背包空间足够放下），背包的剩余容量会减小 $v_i$ ，背包中物品的总价值会增大 $w_i$ ，此时背包的价值为 $f_{i,j}=f_{i-1,j-v_i}+w_i$
故背包的最大价值为 $f_{i,j}=\max(f_{i-1,j},f_{i-1,j-v_i}+w_i)$

状态转移方程： $f_{i,j}=\max(f_{i-1,j},f_{i-1,j-v_i}+w_i)$

int N,V;
int v[M],w[M];
int f[M][M];
int main(){
    cin>>N>>V;
    for(int i=1;i<=N;++i){
        cin>>v[i]>>w[i];
    }
    for(int i=1;i<=N;++i){
        for(int j=0;j<=V;++j){
            f[i][j]=f[i-1][j];
            if(j>=v[i]) f[i][j]=max(f[i-1][j],f[i-1][j-v[i]]+w[i]);
        }
    }
    cout<<f[N][V];
    return 0;
}

**滚动数组优化：**由于对 $f_i$ 有影响的只有 $f_{i-1}$ ，可以去掉第一维，直接用 $f_j$ 来表示处理到当前物品时背包容量为 $j$ 的最大价值，得出以下方程：

$f_j=\max(f_j,f_{j-v_i}+w_i)$

$j$ 应该倒序枚举，从 $V$ 枚举到 $v_i$
时间复杂度 $O(NV)$ ，空间复杂度 $O(V)$

for(int i=1;i<=N;++i){
    for(int j=V;j>=v[i];j--){
        f[j]=max(f[j],f[j-v[i]]+w[i]);
    }
}
cout<<f[V];

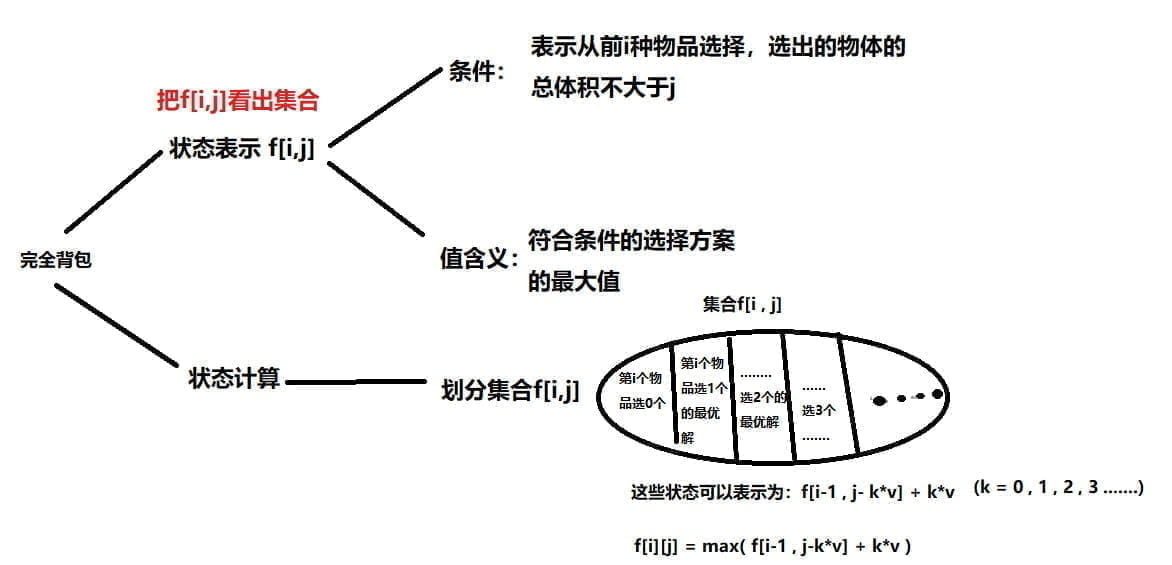
完全背包

完全背包模型与 0-1 背包类似，与 0-1 背包的区别仅在于一个物品可以选取无限次，而非仅能选取一次。

朴素做法暴力算法
- 对于第 $i$ 件物品，枚举其选了多少个来转移
- 共求解 $O(NV)$ 个状态，求解状态 $f_{i,j}$ 的时间是 $O(j/v_i)$ ，时间复杂度 $O(V\sum_{i=1}^N\frac{V}{v_i})$
$\begin{align*}f_{i, j}&=\max _{k=0}^{\lfloor\frac{j}{v_i}\rfloor}\left(f_{i-1, j-k \times v_{i}}+w_{i} \times k\right)\\ &=\max(f_{i-1,j}\;,\;f_{i-1,j-v_i}+w_i\;,\;f_{i-1,j-2v_i}+2w_i\;,\;\cdots\;,\;f_{i-1,j-\lfloor\frac{j}{v_i}\rfloor v_i}+\lfloor\frac{j}{v_i}\rfloor w_i)\end{align*}$

优化时间 $O(NV)$

$\begin{align*} f_{i, j}&=\max(f_{i-1,j}\;,\;f_{i-1,j-v_i}+w_i\;,\;f_{i-1,j-2v_i}+2w_i\;,\;\cdots\;,\;f_{i-1,j-\lfloor\frac{j}{v_i}\rfloor v_i}+\lfloor\frac{j}{v_i}\rfloor w_i)\\ f_{i, j-v_i}&=\max(f_{i-1,j-v_i}\;,\;f_{i-1,j-2v_i}+w_i\;,\;f_{i-1,j-3v_i}+2w_i\;,\;\cdots\;,\;f_{i-1,j-v_i-\lfloor\frac{j-v_i}{v_i}\rfloor v_i}+\lfloor\frac{j-v_i}{v_i}\rfloor w_i)\\ &=\max(f_{i-1,j-v_i}\;,\;f_{i-1,j-2v_i}+w_i\;,\;f_{i-1,j-3v_i}+2w_i\;,\;\cdots\;,\;f_{i-1,j-\lfloor\frac{j}{v_i}\rfloor v_i}+(\lfloor\frac{j}{v_i}\rfloor -1)w_i) \end{align*}$

则有

$\begin{align*} f_{i, j}&=\max _{k=0}^{\lfloor\frac{j}{v_i}\rfloor}\left(f_{i-1, j-k \times v_{i}}+w_{i} \times k\right)\\ &=\max(f_{i-1,j}\;,\;f_{i-1,j-v_i}+w_i\;,\;f_{i-1,j-2v_i}+2w_i\;,\;\cdots\;,\;f_{i-1,j-\lfloor\frac{j}{v_i}\rfloor v_i}+\lfloor\frac{j}{v_i}\rfloor w_i)\\ &=\max(f_{i-1,j}\;,\;\max(f_{i-1,j-v_i}+w_i\;,\;f_{i-1,j-2v_i}+2w_i\;,\;\cdots\;,\;f_{i-1,j-\lfloor\frac{j}{v_i}\rfloor v_i}+\lfloor\frac{j}{v_i}\rfloor w_i)) \end{align*}$

即

$f_{i,j}=\max(f_{i-1,j}\;,\;f_{i,j-v_i}+w_i)$

int N,V;
const int M=1010;
int v[M],w[M];
int f[M][M];
int main(){
    cin>>N>>V;
    for(int i=1;i<=N;++i){
        cin>>v[i]>>w[i];
    }
    for(int i=1;i<=N;++i){
        for(int j=0;j<=V;++j){
            f[i][j]=f[i-1][j];
            if(j>=v[i]) f[i][j]=max(f[i-1][j],f[i][j-v[i]]+w[i]);
        }
    }
    cout<<f[N][V];
    return 0;
}

滚动数组优化空间到一维

$f_{j}=\max(f_{j},f_{j-v_i}+w_i)\\ j\;\text{从小到大正向枚举}$
1
2
3
4
5
6
for(int i=1;i<=N;++i){
for(int j=v[i];j<=V;++j){
f[j]=max(f[j],f[j-v[i]]+w[i]);
}
}
cout<<f[V];

多重背包

多重背包也是 0-1 背包的一个变式。与 0-1 背包的区别在于每种物品有 $s_i$ 个，而非一个。

朴素做法 $O(V\sum_{i=1}^Ns_i)$

把「每种物品选 $s_i$ 次」等价转换为「有 $s_i$ 个相同的物品，每个物品选一次」。

这样就转换成了一个 0-1 背包模型。

状态转移方程：

$\begin{align*} f_{i,j}&=\max(f_{i-1,j}\;,\;f_{i-1,j-v_i}+w_i\;,\;f_{i-1,j-2v_i}+2w_i\;,\;\cdots\;,\;f_{i-1,j-s_iv_i}+s_iw_i)\\ &=\max_{k=0}^{s_i}(f_{i-1,j-kv_i}+kw_i) \end{align*}$

int N,V;
int v[M],w[M],s[M];
int f[M][M];
int main(){
    cin>>N>>V;
    for(int i=1;i<=N;++i){
        cin>>v[i]>>w[i]>>s[i];
    }
    for(int i=1;i<=N;++i){
        for(int j=0;j<=V;++j){
            for(int k=0;k<=s[i]&&k*v[i]<=j;++k){
                f[i][j]=max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]);
            }
        }
    }
    cout<<f[N][V];
    return 0;
}

二进制分组优化

利用二进制的思想, 我们把第 $i$ 种物品换成若干件物品, 使得原问题中第 $i$ 种物品可取的每种策略「取 $0\cdots s_{i}$ 件」均能等价于取若干件代换以后的物品。另外, 取超过 $s_{i}$ 件的策略必不能出现。
方法是：将第 $i$ 种物品分成若干件 01 背包中的物品, 其中每件物品有一个系数。这件物品的费用和价值均是原来的费用和价值乘以这个系数。
- 令这些系数分别为 $1,2^1,2^{2}, \cdots ,2^{k-1}, s_{i}-2^{k}+1$ , 且 $k$ 是满足 $1+2^1+2^2+\cdots+2^{k-1}=2^{k}-1\leq s_{i}$ 的最大整数，即 $k=\lfloor \log_2(s_i+1) \rfloor$ 。
- 分成的这几件物品的系数和为 $s_{i}$ , 表明不可能取多于 $s_{i}$ 件的第 $i$ 种物品。
- 另外这种方法也能保证对于 $0 \ldots s_{i}$ 间的每一个整数，均可以用若干个系数的和表示。这里算法正确性的证明可以分 $0 \ldots 2^{k-1}$ 和 $2^{k} \cdots s_{i}$ 两段来分别讨论得出。
这样就将第 $i$ 个物品分成了 $O(\log{s_i})$ 个物品，复杂度降为 $O(V\sum_{i=1}^N\log{s_i})$

int N,V;
int v[M],w[M],idx;
int f[MM];
int main(){
    cin>>N>>V;
    for(int i=1;i<=N;++i){
        int a,b,s;
        cin>>a>>b>>s;
        int k=1;
        while(k<s){
            v[++idx]=k*a;
            w[idx]=k*b;
            s-=k;
            k*=2;
        }
        if(s){
            v[++idx]=s*a;
            w[idx]=s*b;
        }
    }
    for(int i=1;i<=idx;++i){
        for(int j=V;j>=v[i];--j){
            f[j]=max(f[j],f[j-v[i]]+w[i]);
        }
    }
    cout<<f[V];
    return 0;
}

分组背包

所谓分组背包，就是将物品分组，每组的物品相互冲突，最多只能选一个物品放进去。

捕获.PNG

其实是从「在所有物品中选择一件」变成了「从当前组中选择一件」，于是就对每一组进行一次 0-1 背包就可以了。
如何进行存储。用 $v_{i,k}\;,\;w_{i,k}$ 分别表示第 $i$ 组的第 $k$ 件物品的体积和价值，再用 $s_i$ 表示第 $i$ 组物品有多少个。

int N,V;
int v[M][M],w[M][M],s[M];
int f[M];
int main(){
    cin>>N>>V;
    for(int i=1;i<=N;++i){
        cin>>s[i];
        for(int k=1;k<=s[i];++k){
            cin>>v[i][k]>>w[i][k];
        }
    }
    for(int i=1;i<=N;++i){
        for(int j=V;j>=0;--j){
            for(int k=1;k<=s[i];++k){
                if(j>=v[i][k]) f[j]=max(f[j],f[j-v[i][k]]+w[i][k]);
            }
        }
    }
    cout<<f[V];
    return 0;
}

初始化细节

要求恰好装满背包,那么在初始化时除了 $F[0]$ 为 0，其它 $F[1\cdots V]$ 均设为 $-\infty$ ，这样就可以保证最终得到的 $F[V]$ 是一种恰好装满背包的最优解。
如果并没有要求必须把背包装满, 而是只希望价格尽量大, 初始化时应该将 $F[0][0\cdots V]$ 全部设为 0 。
初始化的 $F$ $F$ 数组事实上就是在没有任何物品可以放入背包时的合法状态。
- 如果要求背包恰好装满, 那么此时只有容量为 0 的背包可以在什么也不装且价值为 0 的情况下被“恰好装满”，其它容量的背包均没有合法的解，属于未定义的状态，应该被赋值为 $-\infty$ 了。
- 如果背包并非必须被装满，那么任何容量的背包，都有一个合法解“什么都不装”，这个解的价值为 0 ，所以初始时状态的值也就全部为 0 了。

线性DP

数字三角形

#include<iostream>
#include<cstring>
using namespace std;
const int N=510;
int n;
int f[N][N],a[N][N];
int main(){
    cin>>n;
    for(int i=1;i<=n;++i){
        for(int j=1;j<=i;++j){
            cin>>a[i][j];
        }
    }
    memset(f,0xc0,sizeof f);
    f[1][1]=a[1][1];
    for(int i=2;i<=n;++i){
        for(int j=1;j<=i;++j){
            f[i][j]=max(f[i-1][j-1],f[i-1][j])+a[i][j];
        }
    }
    int res=0xc0c0c0c0;
    for(int i=1;i<=n;++i) res=max(res,f[n][i]);
    cout<<res;
    return 0;
}

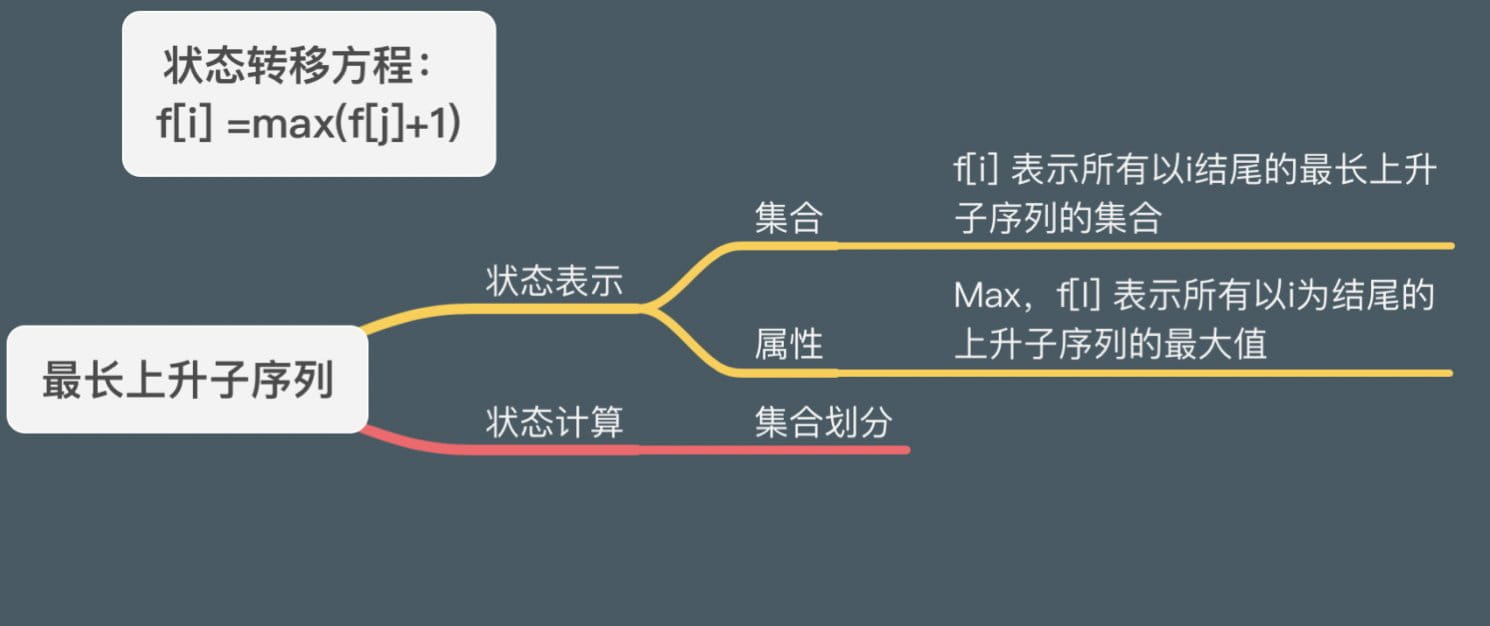
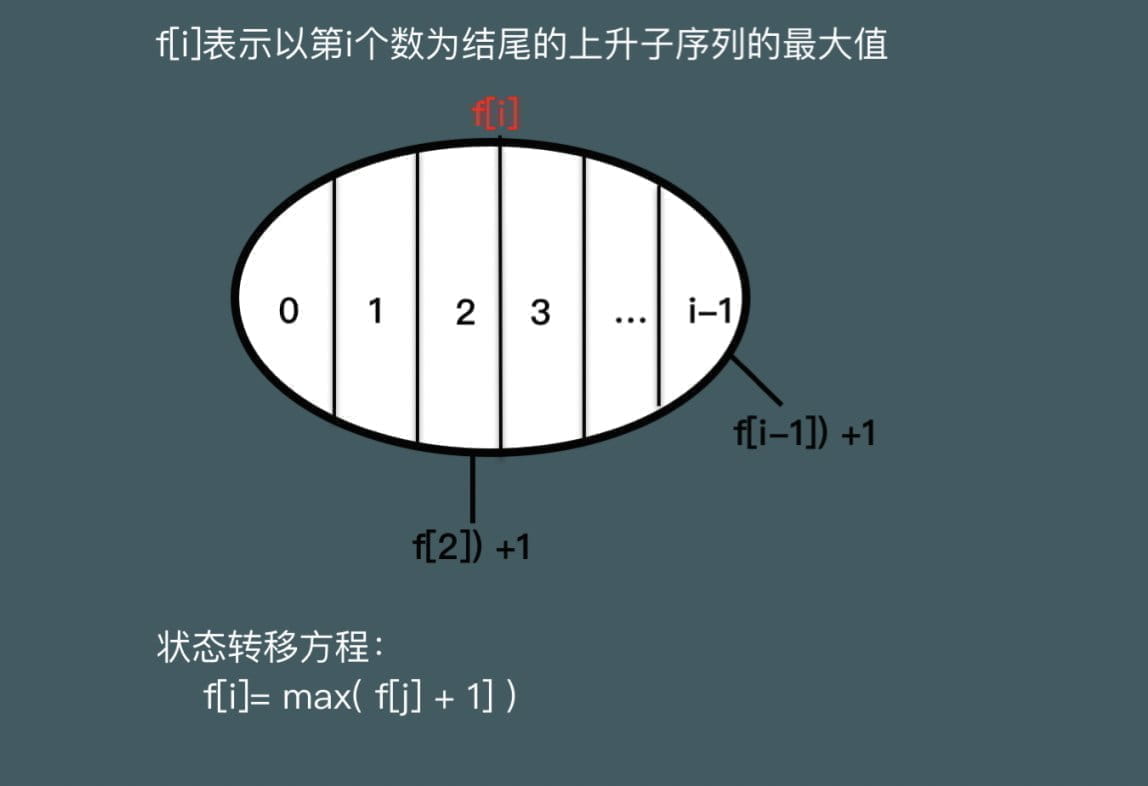
最长上升子序列

int n;
int f[N],a[N],path[N];
int main(){
    cin>>n;
    for(int i=1;i<=n;++i)cin>>a[i];
    int t=1;
    for(int i=1;i<=n;++i){
        for(int j=0;j<i;++j){
            if(j==0||a[j]<a[i]){
                if(f[i]<f[j]+1){
                    f[i]=f[j]+1;
                    path[i]=j;
                }
            }
        }
        if(f[i]>f[t]) t=i;
    }
    cout<<"Length:"<<f[t]<<endl<<"Path:";
    while(t){
        cout<<a[t]<<" ";
        t=path[t];
    }
}

int n,a[N],stk[N],tt;
int main(){
    cin>>n;
    for(int i=1;i<=n;++i){
        cin>>a[i];
        int l=1,r=tt+1;//扩大右边界至越界下标
        while(l<r)
            int mid=l+r>>1;
            if(stk[mid]>=a[i]){
                r=mid;
            }else{
                l=mid+1;
            }
        }
        if(r==tt+1)stk[++tt]=a[i];//越界，则不存在>=a[i]的值
        else stk[r]=a[i];//stk[r]为>=a[i]的最小值
    }
    cout<<tt<<endl;
}

最短编辑距离

char a[N],b[N];
int f[N][N];
int main(){
    int n,m;
    cin>>n>>a+1>>m>>b+1;
    for(int i=1;i<=n;++i)f[i][0]=i;
    for(int j=1;j<=m;++j)f[0][j]=j;
    for(int i=1;i<=n;++i){
        for(int j=1;j<=m;++j){
            f[i][j]=min(f[i-1][j],f[i][j-1])+1;
            f[i][j]=min(f[i][j],f[i-1][j-1]+(a[i]!=b[j]));
        }
    }
    cout<<f[n][m];

}

零散知识点

模 $1e9+7$

$1e9+7$ 是质数，且小于 $2^{30}$
如果原数是 $int$ ，那么所有模过的数之间的加法操作必然不会溢出 $int$
如果原数是 $long\;long$ ，那么所有模过的数两两相乘必然不会溢出 $long\;long$

无穷大无穷小

#include<cstring>
const int INF=0x3f3f3f3f;
const int nINF=0xc0c0c0c0;
int a[10],b[10];
memset(a,0x3f,sizeof a);
memset(b,0xc0,sizeof b);

取整

$>>1$ 等于÷2，是向下取整
/2是向0取整
$\lceil \frac{m}{n} \rceil=\left\lfloor\frac{m-1}{n}\right\rfloor+1$
$\left\lfloor\frac{m}{n}\right\rfloor=\lceil \frac{m+1}{n} \rceil -1$

调和级数

$\sum_{k=1}^n\frac{1}{k}=\ln{n}+C=O(\log{n})$

判断奇偶

if (x & 1) {
    cout << "x是奇数" << endl;
} else {
    cout << "x是偶数" << endl;
}

$2^n$

1	int x = 1 << n;

位运算

<< >> 位移运算符优先级小于±*/
数异或0等于自身，异或1…1等取反
将数n的第j位取反：n^(1<<j)
获取数n的第j位 n>>j&1
返回n的最后一位1：lowbit(n) = n & -n

ListNode* 小顶堆

struct cmp {
	bool operator()(const ListNode* a, const ListNode* b) const {
		return a->val > b->val;
	}
};
priority_queue<ListNode*, vector<ListNode*>, cmp> heap;

遍历转移

1 2	while (k && nums[k - 1] >= x) --k; while (t + 1 < nums.size() && nums[t + 1] > x) ++t;

去重

1
2
3

sort(a.begin(), a.end());
auto newend = unique(a.begin(), a.end());
a.erase(unique(newend, a.end());