参考《算法竞赛进阶指南》 、AcWing题库
区间DP
到目前为止, 我们介绍的线性 DP一般从初态开始, 沿着阶段的扩张向某个方向递 推, 直至计算出目标状态。区间 DP 也属于线性 DP 中的一种, 它以 “区间长度” 作为 DP 的 “阶段”, 使用两个坐标 (区间的左、右端点) 描述每个维度。在区间 DP 中, 一个状态由若干个比它更小且包含于它的区间所代表的状态转移而来, 因此区间 DP 的 决策往往就是划分区间的方法。区间 DP 的初态一般就由长度为 1 的 “元区间” 构成。 这种向下划分、再向上递推的模式与某些树形结构, 例如第 0 × 43 0 \times 43 0 × 43
题目描述
设有 N N N 1 , 2 , 3 , … , N 1,2,3,…,N 1 , 2 , 3 , … , N
每堆石子有一定的质量,可以用一个整数来描述,现在要将这 N N N
每次只能合并相邻的两堆,合并的代价为这两堆石子的质量之和,合并后与这两堆石子相邻的石子将和新堆相邻,合并时由于选择的顺序不同,合并的总代价也不相同。
例如有 4 4 4 1 3 5 2, 我们可以先合并 1 、 2 1、2 1 、 2 4 4 4 4 5 2, 又合并 1 , 2 1,2 1 , 2 9 9 9 9 2 ,再合并得到 11 11 11 4 + 9 + 11 = 24 4+9+11=24 4 + 9 + 11 = 24
如果第二步是先合并 2 , 3 2,3 2 , 3 7 7 7 4 7,最后一次合并代价为 11 11 11 4 + 7 + 11 = 22 4+7+11=22 4 + 7 + 11 = 22
问题是:找出一种合理的方法,使总的代价最小,输出最小代价。
输入格式
第一行一个数 N N N N N N
第二行 N N N 1000 1000 1000
输出格式
输出一个整数,表示最小代价。
数据范围
1 ≤ N ≤ 300 1 \le N \le 300 1 ≤ N ≤ 300
输入样例 :
输出样例 :
算法分析
若最初的第 l l l r r r l ∼ r l \sim r l ∼ r l l l r r r [ l , r ] [l, r] [ l , r ] l ∼ r l \sim r l ∼ r ∑ i = l r A i \sum_{i=l}^{r} A_{i} ∑ i = l r A i k ( l ≤ k < r ) k(l \leq k<r) k ( l ≤ k < r ) l ∼ k l \sim k l ∼ k [ l , k ] ) [l, k]) [ l , k ]) k + 1 ∼ r k+1 \sim r k + 1 ∼ r [ k + 1 , r ] ) [k+1, r]) [ k + 1 , r ]) [ l , r ] [l, r] [ l , r ]
对应到动态规划中, 就意味着两个长度较小的区间上的信息向一个更长的区间发 生了转移,划分点 k k k l e n len l e n l e n = r − l + 1 l e n=r-l+1 l e n = r − l + 1
设 F [ l , r ] F[l, r] F [ l , r ] l l l r r r
F [ l , r ] = min l ≤ k < r { F [ l , k ] + F [ k + 1 , r ] } + ∑ i = l r A i F[l, r]=\min _{l \leq k<r}\{F[l, k]+F[k+1, r]\}+\sum_{i=l}^{r} A_{i}
F [ l , r ] = l ≤ k < r min { F [ l , k ] + F [ k + 1 , r ]} + i = l ∑ r A i
初值: ∀ l ∈ [ 1 , N ] , F [ l , l ] = A l \forall l \in[1, N], F[l, l]=A_{l} ∀ l ∈ [ 1 , N ] , F [ l , l ] = A l
目标: F [ 1 , N ] F[1, N] F [ 1 , N ]
我们在分组背包最后强调, 编程实现动态规划的状态转移方程时, 务必分清阶段、状态与决策, 三者应该按照从外到内的顺序依次循环。对于 ∑ i = l r A i \sum_{i=l}^{r} A_{i} ∑ i = l r A i
Solution
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 #include <iostream> #include <cstring> using namespace std;const int N = 310 ;int f[N][N];int a[N],s[N];int main () int n; cin >> n; for (int i = 1 ; i <= n; ++i) cin >> a[i]; memset (f, 0x3f , sizeof f); for (int i = 1 ; i <= n; ++i) { s[i] = s[i - 1 ] + a[i]; f[i][i] = 0 ; } for (int len = 2 ; len <= n; ++len) { for (int l = 1 ; l + len - 1 <= n; ++l) { int r = l + len - 1 ; for (int k = l; k < r; ++k) { f[l][r] = min (f[l][r], f[l][k] + f[k + 1 ][r]); } f[l][r] += s[r] - s[l - 1 ]; } } cout << f[1 ][n]; }
题目描述
将 n n n
规定每次只能选相邻的两堆合并成新的一堆,并将新的一堆的石子数记做该次合并的得分。
请编写一个程序,读入堆数 n n n
选择一种合并石子的方案,使得做 n − 1 n-1 n − 1
选择一种合并石子的方案,使得做 n − 1 n-1 n − 1
输入格式
第一行包含整数 n n n n n n
第二行包含 n n n
输出格式
输出共两行:
第一行为合并得分总和最小值,
第二行为合并得分总和最大值。
数据范围
1 ≤ n ≤ 200 1 \le n \le 200 1 ≤ n ≤ 200
输入样例 :
输出样例 :
算法分析
拓展:
如果每轮合并的石子 可以是任意 的 两堆 石子,那么用到的就是经典的 Huffman Tree 的二叉堆模型
如果每轮合并的石子 可以是任意 的 n n n Huffman Tree 的 n n n
以上两种题型可以参考:
二叉堆:148. 合并果子
n n n 149. 荷马史诗
回归本题,本题要求每轮合并的石子 必须是相邻的 两堆石子,因此不能采用 Huffman Tree 的模型
这类限制只能合并相邻两堆石子的模型,用到的是经典的 区间DP 模型
考虑如何设定 动态规划 的阶段,既可以表示出初始每个石子的费用,也可以表示出合并后整个堆的费用
不妨把当前合并的石子堆的大小作为DP的阶段
这样 l e n = 1 len=1 l e n = 1 l e n = n len=n l e n = n
这种阶段设置方法保证了我们每次合并两个区间时,他们的所有子区间的合并费用都已经被计算出来了
阶段设定好后,考虑如何记录当前的状态,无外乎就两个参数:
石子堆的左端点 l l l
石子堆的右端点 r r r
状态表示—集合f l e n , l , r : f_{len,l,r}: f l e n , l , r : 当前合并的石子堆的大小为 l e n len l e n l l l r r r
状态表示—属性f l e n , l , r : f_{len,l,r}: f l e n , l , r : 方案的费用最大/最小(本题两者都要求)
状态计算—f l e n , l , r : f_{len,l,r}: f l e n , l , r :
{ 计算最大值的转移: f l e n , l , r = m a x ( f k − l + 1 , l , k + f l e n − ( k − l + 1 ) , k + 1 , r + c o s t l , r ) ( l ≤ k < r ) 计算最小值的转移: f l e n , l , r = m i n ( f k − l + 1 , l , k + f l e n − ( k − l + 1 ) , k + 1 , r + c o s t l , r ) ( l ≤ k < r ) \begin{cases} 计算最大值的转移:f_{len,l,r} = max(f_{k-l+1,l,k} + f_{len-(k-l+1),k+1,r} + cost_{l,r}) \quad (l \le k \lt r) \\ 计算最小值的转移:f_{len,l,r} = min(f_{k-l+1,l,k} + f_{len-(k-l+1),k+1,r} + cost_{l,r}) \quad (l \le k \lt r) \end{cases}
{ 计算最大值的转移: f l e n , l , r = ma x ( f k − l + 1 , l , k + f l e n − ( k − l + 1 ) , k + 1 , r + cos t l , r ) ( l ≤ k < r ) 计算最小值的转移: f l e n , l , r = min ( f k − l + 1 , l , k + f l e n − ( k − l + 1 ) , k + 1 , r + cos t l , r ) ( l ≤ k < r )
初始状态: f 1 , i , i ( 1 ≤ i ≤ n ) f_{1,i,i} \quad (1\le i \le n) f 1 , i , i ( 1 ≤ i ≤ n )
目标状态: f n , 1 , n f_{n,1,n} f n , 1 , n
在区间DP中,我们也常常省去 l e n len l e n
因为 r − l + 1 = l e n r-l+1 = len r − l + 1 = l e n l l l r r r
根据线性代数中方程的解的基本概念,我们就可以删掉 l e n len l e n
但为了方便读者理解,以及介绍区间DP的阶段是如何划分的,我还是写了出来
以上就是所有有关石子合并的区间DP分析
在考虑一下本题的 环形相邻 情况如何解决,方案有如下两种:
我们可以枚举环中分开的位置,将环还原成链,这样就需要枚举 n n n O ( n 4 ) O(n^4) O ( n 4 )
我们可以把链延长两倍,变成 2 n 2n 2 n i i i i + 1 i+1 i + 1 区间DP 模板,但对于 阶段 l e n len l e n n n n 状态的定义 ,最终可以得到所求的方案,时间复杂度为 O ( n 3 ) O(n^3) O ( n 3 )
一般常用的都是第二种方法,我也只会演示第二种方法的写法,对第一种有兴趣的读者可以自行尝试
时间复杂度:O ( n 3 ) O(n^3) O ( n 3 )
Solution
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 #include <iostream> #include <cstring> using namespace std;const int N = 205 ;int maxf[N * 2 ][N * 2 ];int minf[N * 2 ][N * 2 ];int a[N * 2 ], s[N * 2 ];int main () int n; cin >> n; for (int i = 1 ; i <= n; ++i) cin >> a[i], a[i + n] = a[i]; memset (maxf, 0xc0 , sizeof maxf); memset (minf, 0x3f , sizeof minf); for (int i = 1 ; i <= 2 * n; ++i) { maxf[i][i] = minf[i][i] = 0 ; s[i] = s[i - 1 ] + a[i]; } for (int len = 2 ; len <= n; ++len) { for (int l = 1 ; r = l + len - 1 , r <= 2 * n; ++l) { for (int k = l; k < r; ++k) { minf[l][r] = min (minf[l][r], minf[l][k] + minf[k + 1 ][r]); maxf[l][r] = max (maxf[l][r], maxf[l][k] + maxf[k + 1 ][r]); } minf[l][r] += s[r] - s[l - 1 ]; maxf[l][r] += s[r] - s[l - 1 ]; } } int minv = 0x3f3f3f3f , maxv = 0xc0c0c0c0 ; for (int l = 1 ; l + n - 1 <= 2 * n; ++l) { int r = l + n - 1 ; minv = min (minf[l][r], minv); maxv = max (maxf[l][r], maxv); } cout << minv << endl << maxv << endl; }
题目描述
在 Mars 星球上,每个 Mars 人都随身佩带着一串能量项链,在项链上有 N N N
能量珠是一颗有头标记与尾标记的珠子,这些标记对应着某个正整数。
并且,对于相邻的两颗珠子,前一颗珠子的尾标记一定等于后一颗珠子的头标记。
因为只有这样,通过吸盘(吸盘是 Mars 人吸收能量的一种器官)的作用,这两颗珠子才能聚合成一颗珠子,同时释放出可以被吸盘吸收的能量。
如果前一颗能量珠的头标记为 m m m r r r r r r n n n m × r × n m \times r \times n m × r × n m m m n n n
需要时,Mars 人就用吸盘夹住相邻的两颗珠子,通过聚合得到能量,直到项链上只剩下一颗珠子为止。
显然,不同的聚合顺序得到的总能量是不同的,请你设计一个聚合顺序,使一串项链释放出的总能量最大。
例如:设 N = 4 N=4 N = 4 4 4 4 ( 2 , 3 ) ( 3 , 5 ) ( 5 , 10 ) ( 10 , 2 ) (2,3) (3,5) (5,10) (10,2) ( 2 , 3 ) ( 3 , 5 ) ( 5 , 10 ) ( 10 , 2 )
我们用记号 ⊕ ⊕ ⊕ ( j ⊕ k ) (j⊕k) ( j ⊕ k ) j j j k k k
第 4 、 1 4、1 4 、 1 ( 4 ⊕ 1 ) = 10 × 2 × 3 = 60 (4⊕1)=10 \times 2 \times 3=60 ( 4 ⊕ 1 ) = 10 × 2 × 3 = 60
这一串项链可以得到最优值的一个聚合顺序所释放的总能量为 ( ( 4 ⊕ 1 ) ⊕ 2 ) ⊕ 3 ) = 10 × 2 × 3 + 10 × 3 × 5 + 10 × 5 × 10 = 710 ((4 \oplus 1) \oplus 2) \oplus 3) = 10 \times 2 \times 3+10 \times 3 \times 5+10 \times 5 \times 10=710 (( 4 ⊕ 1 ) ⊕ 2 ) ⊕ 3 ) = 10 × 2 × 3 + 10 × 3 × 5 + 10 × 5 × 10 = 710
输入格式
输入的第一行是一个正整数 N N N
第二行是 N N N 1000 1000 1000 i i i i i i i < N i<N i < N i i i i + 1 i+1 i + 1 N N N 1 1 1
至于珠子的顺序,你可以这样确定:将项链放到桌面上,不要出现交叉,随意指定第一颗珠子,然后按顺时针方向确定其他珠子的顺序。
输出格式
输出只有一行,是一个正整数 E E E
数据范围
4 ≤ N ≤ 100 4 \le N \le 100 4 ≤ N ≤ 100 1 ≤ E ≤ 2.1 × 1 0 9 1 \le E \le 2.1 \times 10^9 1 ≤ E ≤ 2.1 × 1 0 9
输入样例 :
输出样例 :
算法分析
给定 N N N ( w i , 1 , w i , 2 ) (w_{i,1}, w_{i,2}) ( w i , 1 , w i , 2 )
其中 w i , 1 w_{i,1} w i , 1 i i i i − 1 i-1 i − 1 能量 的其中一个参数
当然 w i , 2 w_{i,2} w i , 2 i i i i + 1 i+1 i + 1 能量 的其中一个参数
魔法石是顺序 且环形 摆放的,每次可以融合相邻 两个魔法石
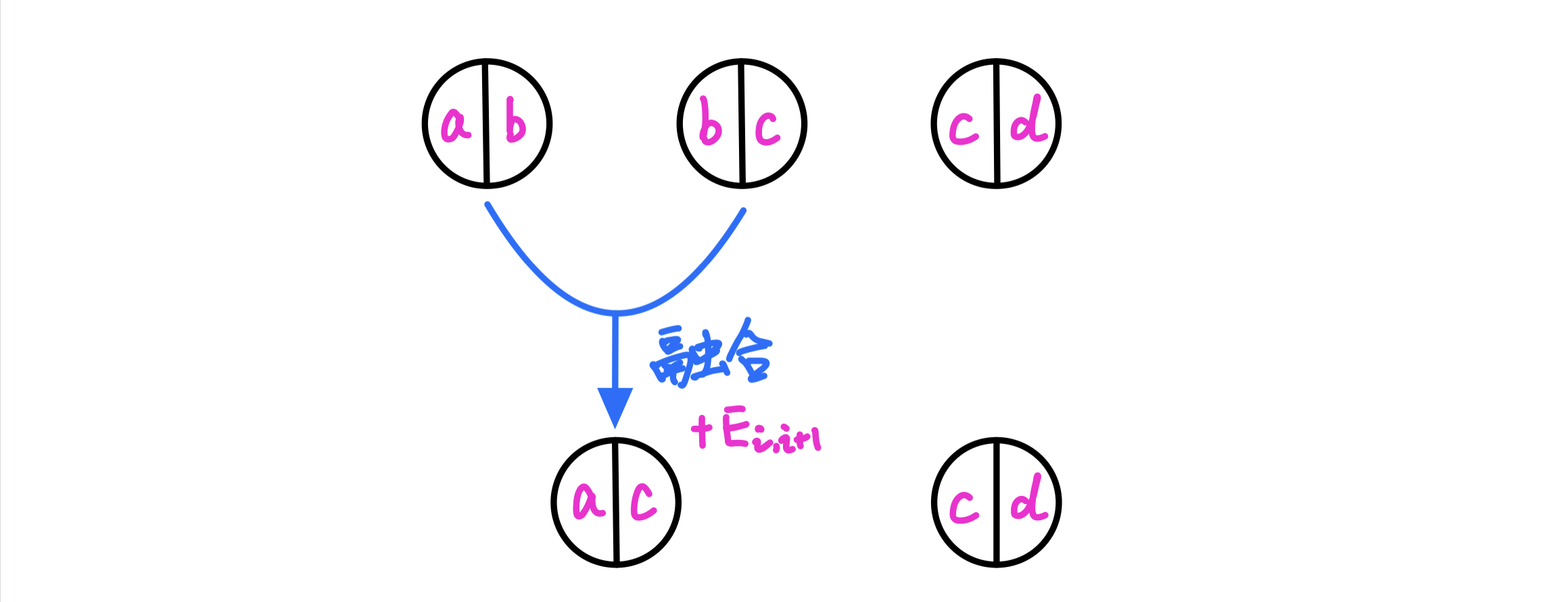
融合两个能量石 i , i + 1 i,i+1 i , i + 1
E i , i + 1 = w i , 1 × ( w i , 2 或 w i + 1 , 1 ) × w i + 1 , 1 E_{i,i+1} = w_{i,1} \times (w_{i,2} 或 w_{i+1,1}) \times w_{i+1,1}
E i , i + 1 = w i , 1 × ( w i , 2 或 w i + 1 , 1 ) × w i + 1 , 1
融合后左侧 魔法石的第一个参数 和右侧 魔法石的第二个参数 合并成为一颗新的 魔法石
具体如下图所示:
求最终把所有石头融合成一个石头时,产生的最大能量值
本题可以把区间长度作为搜索的阶段来进行记忆话搜索,因此我们也可以采用 区间DP 的方式来处理
这题和 环形石子合并 十分相似,但又不尽相同
在 环形石子 中,每个石头只有单一的参数,而本题有两个参数,也就意味着我们需要在细节上做出改变
经过观察我们发现,合并两个石头 ( a , b ) , ( b , c ) (a,b),(b,c) ( a , b ) , ( b , c ) ( a , c ) (a,c) ( a , c )
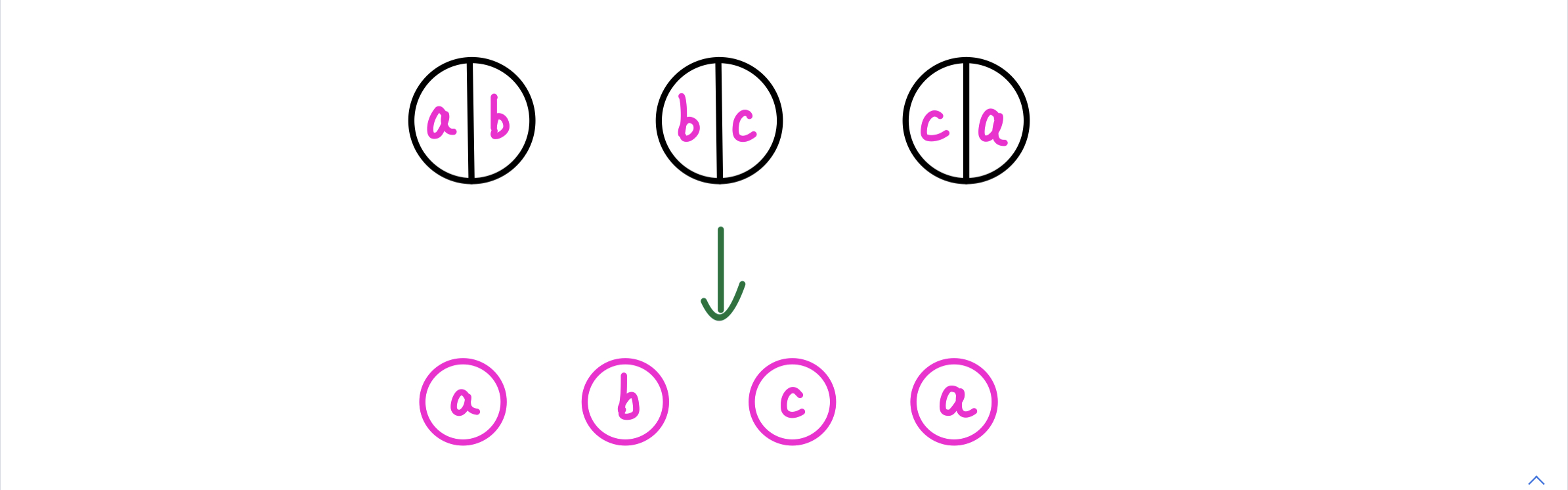
因此我们可以离散的来存储每个参数,具体如下所示:
这样 状态表示 就更新为:当前合并的石子堆的左端石头的左参数是 l l l r r r
这样对应的 初始状态 本来应该是一个有着 二元属性 的石头,现在就变成了长度为 2 2 2
这样合并区间后,需要记录的新石头的参数也刚好是 区间的两端 对应的参数,如下图所示:
而且这里我们的转移方程也要修改为 f l , r = m a x ( f l , k + f k , r + E l , r ) f_{l,r} = max(f_{l,k} + f_{k,r} + E_{l,r}) f l , r = ma x ( f l , k + f k , r + E l , r )
以往的 区间DP 我们是把区间 [ a , b ] [a,b] [ a , b ] [ a , k ] 和 [ k + 1 , b ] [a,k] 和 [k+1,b] [ a , k ] 和 [ k + 1 , b ]
因为 同一个石子 只会被合并到 一个石子堆 里
但本题合并魔法石时,分割点 k k k 左侧石子堆的右端点 和 右侧石子堆的左端点 中
因此,参数 k k k [ a , k ] [a,k] [ a , k ] [ k , b ] [k,b] [ k , b ]
此外我们原来只需要合并 n n n n + 1 n+1 n + 1
状态表示—集合f l , r : f_{l,r}: f l , r : 当前合并的石子堆的左端石头的左参数是 l l l r r r
状态表示—属性f l , r : f_{l,r}: f l , r : 方案的费用最大
状态计算—f l , r : f_{l,r}: f l , r :
f l , r = m a x ( f l , k + f k , r + E l , r ) ( l < k < r ) f_{l,r} = max(f_{l,k} + f_{k,r} + E_{l,r}) \quad (l \lt k \lt r)
f l , r = ma x ( f l , k + f k , r + E l , r ) ( l < k < r )
初始状态: f l , l + 1 = 0 ( 1 ≤ l ≤ n ) f_{l,l+1} = 0 \quad(1\le l \le n) f l , l + 1 = 0 ( 1 ≤ l ≤ n )
目标状态: f 1 , n + 1 f_{1,n + 1} f 1 , n + 1
时间复杂度: O ( n 3 ) O(n^3) O ( n 3 )
Solution
预处理每个能量珠,整合成一个物体
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 #include <iostream> #include <cstring> using namespace std;const int N = 105 ;int f[2 * N][2 * N];int a[2 * N];pair<int ,int > w[2 * N]; int main () int n; cin >> n; for (int i = 1 ; i <= n; ++i) cin >> a[i], a[i + n] = a[i]; for (int i = 1 ; i + 1 <= 2 * n; ++i) w[i].first = a[i], w[i].second = a[i + 1 ]; w[2 * n].first = a[2 * n], w[2 * n].second = a[1 ]; for (int len = 2 ; len <= n; ++len) { for (int l = 1 , r; r = l + len - 1 , r <= 2 * n; ++l) { if (l == r) { f[l][r] = 0 ; continue ; } for (int k = l; k < r; ++k) { f[l][r] = max (f[l][r], f[l][k] + f[k + 1 ][r] + w[l].first * w[k].second * w[r].second); } } } int maxv = 0xc0c0c0c0 ; for (int l = 1 ; l + n - 1 <= 2 * n; ++l) maxv = max (f[l][l + n - 1 ], maxv); cout << maxv; }
直接计算,要注意2个数对应一个能量珠
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 #include <iostream> #include <cstring> using namespace std;const int N = 105 ;int f[2 * N][2 * N];int a[2 * N];int main () int n; cin >> n; for (int i = 1 ; i <= n; ++i) cin >> a[i], a[i + n] = a[i]; for (int len = 3 ; len <= n + 1 ; ++len) { for (int l = 1 , r; r = l + len - 1 , r <= 2 * n; ++l) { for (int k = l + 1 ; k < r; ++k) { f[l][r] = max (f[l][r], f[l][k] + f[k][r] + a[l] * a[k] * a[r]); } } } int maxv = 0xc0c0c0c0 ; for (int l = 1 , r; r = l + (n + 1 ) - 1 , r <= 2 * n; ++l) maxv = max (f[l][r], maxv); cout << maxv; }
题目描述
设一个 n n n 1 , 2 , 3 , … , n 1,2,3,…,n 1 , 2 , 3 , … , n 1 , 2 , 3 , … , n 1,2,3,…,n 1 , 2 , 3 , … , n
每个节点都有一个分数(均为正整数),记第 i i i d i d_i d i
subtree的左子树的加分 × × × + + +
若某个子树为空,规定其加分为 1 1 1
叶子的加分就是叶节点本身的分数,不考虑它的空子树。
试求一棵符合中序遍历为(1 , 2 , 3 , … , n 1,2,3,…,n 1 , 2 , 3 , … , n
要求输出:
(1)tree的最高加分
(2)tree的前序遍历
输入格式
第 1 1 1 n n n
第 2 2 2 n n n 0 < 0< 0 < < 100 <100 < 100
输出格式
第 1 1 1 int范围)。
第 2 2 2 n n n
数据范围
n < 30 n < 30 n < 30
输入样例 :
输出样例 :
算法分析
给定一个含有 n n n 中序遍历 序列中每个节点的 权值
定义一棵 子树 的 分数 为 左子树的分数 × 右子树的分数 + 根节点的权值 左子树的分数 \times 右子树的分数 + 根节点的权值 左子树的分数 × 右子树的分数 + 根节点的权值
额外规定 空树 的 分数 为 1 1 1
求一种满足该 中序遍历 的建树方案,使得整棵树的 分数 最大
因为本题是一道与树相关的区间DP,因此本题解采用 记忆化搜索 的思想来分析,抛开常规 动态规划 思路
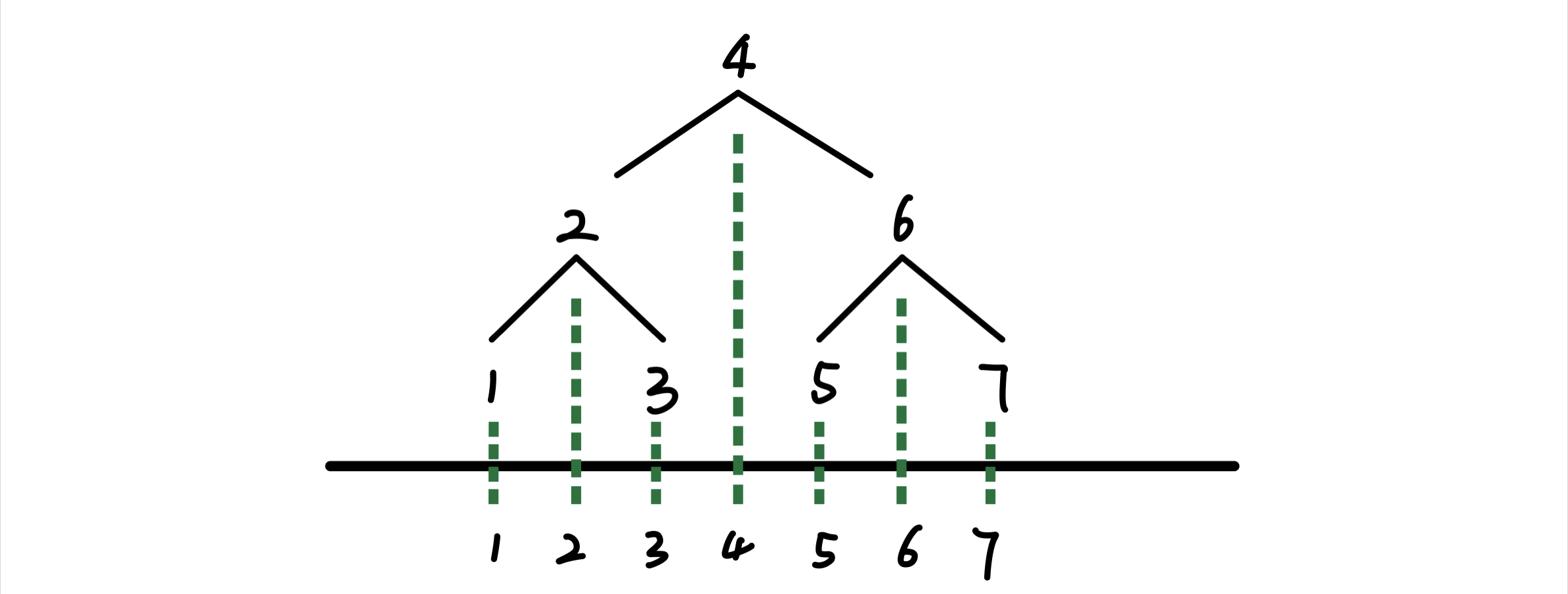
首先读者需要知道一个二叉树的小常识:
二叉树节点 向下投影 ,映射成的数组序列就是 中序遍历序列 ,入下图所示
这也是诱使我们本题采用 区间DP 的一大原因之一(但这篇题解采用 记忆化搜索 思想分析)
借助上图直观的表象,我们发现可以任意的选择 中序遍历 的某一段区间便可生成多棵子树(枚举根节点)
于是我们就会想到 分治 的思想,枚举好根节点后,递归的处理左右区间生成的 最大分数子树
回溯后,利用计算好的子树的分数 相乘,再加上根结点的 权值 ,就可以得出该方案的 最大分数
而直接递归 搜索 的时间复杂度是 O ( n ! ) O(n!) O ( n !)
n × ( n − 1 ) × ⋯ × 1 = n ! n \times (n-1) \times \cdots \times 1 = n! n × ( n − 1 ) × ⋯ × 1 = n ! 1 1 1
因为在这个递归中,有相当大的计算是去处理的 相同的区间
因此我们不妨采用 记忆化搜索 的形式优化掉这些 重复的搜索
考虑用数组 f l , r f_{l,r} f l , r l l l r r r
这样就会 剪枝 掉相当大的冗余 搜索分支
状态表示—集合f l , r : f_{l,r}: f l , r : 当前以 l l l r r r 中序遍历 ,生成树的方案
状态表示—属性f l , r : f_{l,r}: f l , r : 方案的分数最大
状态计算—f l , r : f_{l,r}: f l , r :
f l , r = m a x ( f l , k − 1 × f k + 1 , r + w k ) ( l ≤ k < r ) f_{l,r} = max(f_{l,k - 1} \times f_{k + 1, r} + w_k) \quad (l \le k \lt r)
f l , r = ma x ( f l , k − 1 × f k + 1 , r + w k ) ( l ≤ k < r )
初始状态: f l , l = w l f_{l,l} = w_l f l , l = w l
目标状态: f l , r f_{l,r} f l , r
时间复杂度:O ( n 3 ) O(n^3) O ( n 3 )
Solution
循环
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 #include <iostream> using namespace std;const int N = 35 ;int f[N][N];int a[N];int root[N][N];void dfs (int l, int r) if (l > r) return ; int k = root[l][r]; cout << k << " " ; dfs (l, k - 1 ); dfs (k + 1 , r); } int main () int n; cin >> n; for (int i = 1 ; i <= n; ++i) cin >> a[i]; for (int len = 1 ; len <= n; ++len) { for (int l = 1 ; l + len - 1 <= n; ++l) { int r = l + len - 1 ; if (len == 1 ) { f[l][r] = a[l]; root[l][r] = l; continue ; } for (int k = l; k <= r; ++k) { int left = k == l ? 1 : f[l][k - 1 ]; int right = k == r ? 1 : f[k + 1 ][r]; int score = left * right + a[k]; if (f[l][r] < score) { f[l][r] = score; root[l][r] = k; } } } } cout << f[1 ][n] << endl; dfs (1 , n); }
记忆化搜索
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 #include <iostream> #include <cstring> using namespace std;const int N = 35 ;int f[N][N];int a[N];int root[N][N];int dp (int l, int r) if (f[l][r] != -1 ) return f[l][r]; if (l == r) return root[l][r] = l, f[l][r] = a[l]; if (l > r) return f[l][r] = 1 ; int maxv = 0 ; for (int k = l; k <= r; ++k) { int score = dp (l, k - 1 ) * dp (k + 1 , r) + a[k]; if (score > maxv) { maxv = score; root[l][r] = k; } } return f[l][r] = maxv; } void dfs (int l, int r) if (l > r) return ; int k = root[l][r]; cout << k << " " ; dfs (l, k - 1 ); dfs (k + 1 , r); } int main () int n; cin >> n; for (int i = 1 ; i <= n; ++i) cin >> a[i]; memset (f, -1 , sizeof f); cout << dp (1 , n) << endl; dfs (1 , n); }
题目描述
给定一个具有 N N N 1 1 1 N N N
将这个凸多边形划分成 N − 2 N-2 N − 2
输入格式
第一行包含整数 N N N
第二行包含 N N N 1 1 1 N N N
输出格式
输出仅一行,为所有三角形的顶点权值乘积之和的最小值。
数据范围
N ≤ 50 N \le 50 N ≤ 50 1 0 9 10^9 1 0 9
输入样例 :
输出样例 :
算法分析
这是一个经典的 图形学 问题 — 三角剖分
因为我们现实中常见的一些 多边形图形 存储到计算机中,需要转存为一个个 像素点
那么如何存储一个 多边形 最简单的方案就是把它转化为 多个三角形 进行存储
也就是 三角剖分 问题,不只是 凸多边形 ,还能解决 凹多边形 , 有孔多边形 等问题
对应有 O ( n 3 ) O(n^3) O ( n 3 ) O ( n 2 ) O(n^2) O ( n 2 ) e a r c l i p p i n g ear clipping e a rc l i pp in g O ( n log n ) O(n\log n) O ( n log n ) D e l a u n a y Delaunay De l a u na y
还有很复杂的线性算法
以上和本题都没啥关系,大家有兴趣学习的可以自行翻阅文献和资料
回归本题,本题是一个给定的 凸多边形 求 三角剖分 的最小费用方案
很显然一个 凸多边形的剖分方案 并不唯一:
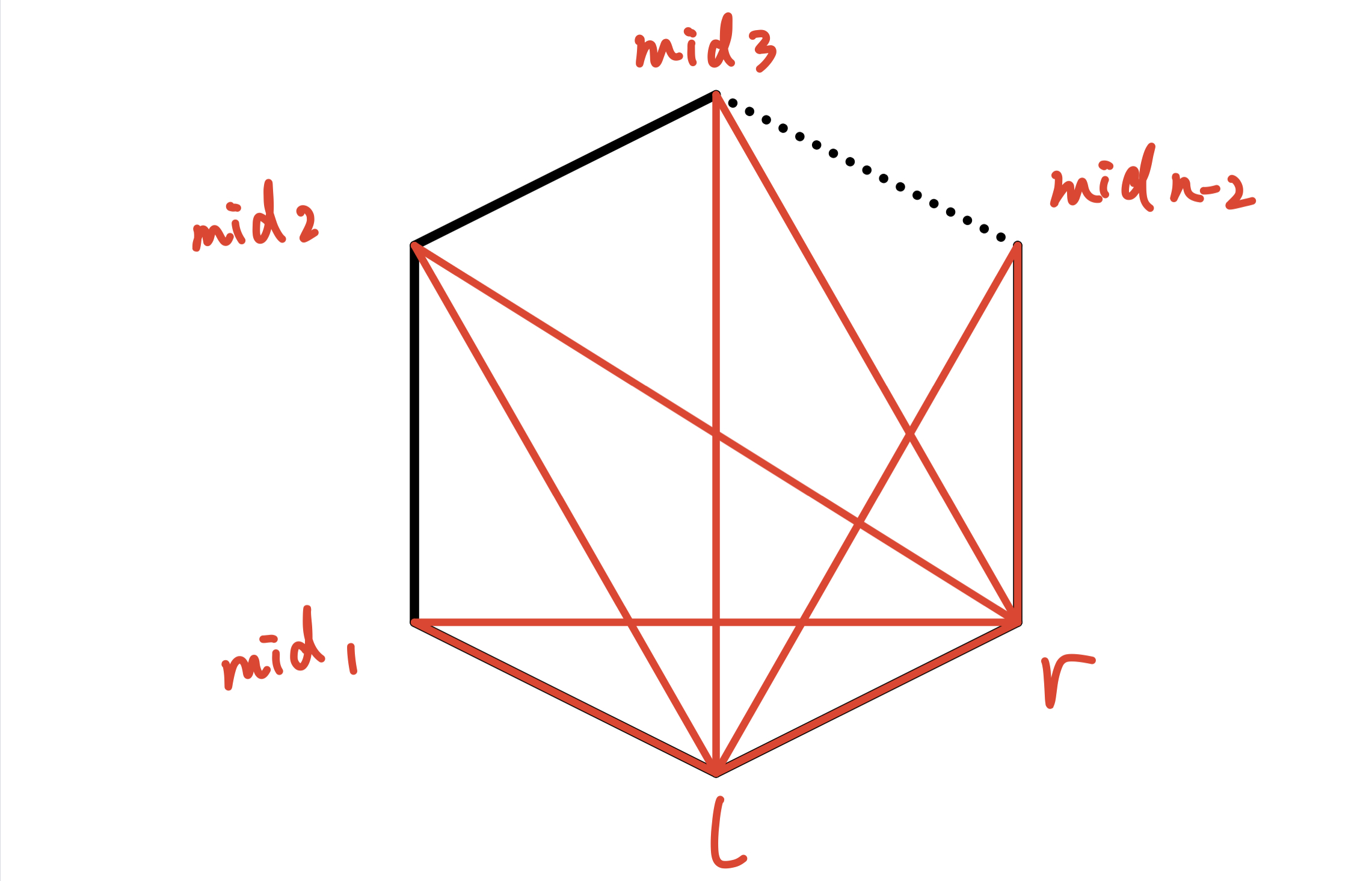
在 选定 多边形中 两个点 后,找出 三角形 的 第三个点 的方案有 n − 2 n-2 n − 2
然后还要分别 划分 他的 左右两块区域
因此我们就会想到用 记忆化搜索 或者 区间DP 来进行处理
状态表示—集合f l , r : f_{l,r}: f l , r : 当前划分到的多边形的左端点是 l l l r r r
状态表示—属性f l , r : f_{l,r}: f l , r : 方案的费用最小
状态计算—f l , r : f_{l,r}: f l , r :
f l , r = m i n ( f l , k + f k , r + w l × w k × w r ) ( l < k < r ) f_{l,r} = min(f_{l,k} + f_{k,r} + w_l \times w_k \times w_r) \quad (l \lt k \lt r)
f l , r = min ( f l , k + f k , r + w l × w k × w r ) ( l < k < r )
区间DP 在状态计算的时候一定要 认真 划分好 边界 和 转移 ,对于不同题目是不一样的
然后本题非常的嚣张,直接用样例的 5 5 5 i n t int in t l o n g l o n g long \; long l o n g l o n g
并且没有 取模 要求,那就只能上 高精度 了 ~用Python了~
时间复杂度: O ( n 3 ) O(n^3) O ( n 3 )
Solution
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 #include <iostream> #include <cstring> #include <vector> #include <algorithm> using namespace std;const int N = 55 ;vector<int > f[N][N]; int w[N];bool cmple (const vector<int > &a, const vector<int > &b) if (a.size () != b.size ()) return a.size () < b.size (); for (int i = a.size () - 1 ; i >= 0 ; --i) { if (a[i] != b[i]) return a[i] < b[i]; } return true ; } vector<int > add (const vector<int > &a, const vector<int > &b) { vector<int > c; int t = 0 ; for (int i = 0 ; i < a.size () || i < b.size (); ++i) { if (i < a.size ()) t += a[i]; if (i < b.size ()) t += b[i]; c.push_back (t % 10 ); t /= 10 ; } while (t) c.push_back (t % 10 ), t /= 10 ; return c; } vector<int > mul (const vector<int > &a, long long b) { vector<int > c; long long t = 0 ; for (int i = 0 ; i < a.size (); ++i) { t += a[i] * b; c.push_back (t % 10 ); t /= 10 ; } while (t) { c.push_back (t % 10 ); t /= 10 ; } return c; } int main () int n; cin >> n; for (int i = 1 ; i <= n; ++i) cin >> w[i]; for (int len = 3 ; len <= n; ++len) { for (int l = 1 , r; (r = l + len - 1 ) <= n; ++l) { for (int k = l + 1 ; k < r; ++k) { auto newval = mul (mul ({w[l]}, w[k]), w[r]); newval = add (add (newval, f[l][k]), f[k][r]); if (f[l][r].empty () || cmple (newval, f[l][r])) { f[l][r] = newval; } } } } auto &ans = f[1 ][n]; for (int i = ans.size () - 1 ; i >= 0 ; --i) cout << ans[i]; }
题目描述
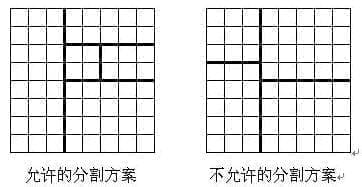
将一个 8 × 8 8 \times 8 8 × 8 ( n − 1 ) (n-1) ( n − 1 ) n n n
原棋盘上每一格有一个分值,一块矩形棋盘的总分为其所含各格分值之和。
现在需要把棋盘按上述规则分割成 n n n
均方差x i x_i x i i i i
请编程对给出的棋盘及 n n n
输入格式
第 1 1 1 n n n
第 2 2 2 9 9 9 8 8 8 100 100 100
输出格式
输出最小均方差值(四舍五入精确到小数点后三位)。
数据范围
1 < n < 15 1 < n < 15 1 < n < 15
输入样例 :
1 2 3 4 5 6 7 8 9 3 1 1 1 1 1 1 1 3 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 0 3
输出样例:
算法分析
这个题目很重要的条件就是:
每次切割都只能沿着棋盘格子的边进行。
关于这个条件的解释,题面中已经写的很清楚了,我就不赘述了。
考虑使均方差 σ = ∑ i = 1 n ( x i − x ˉ ) 2 n \sigma=\sqrt{\dfrac{\sum\limits_{i=1}^{n}(x_i-\bar{x})^2}{n}} σ = n i = 1 ∑ n ( x i − x ˉ ) 2
则考虑使标准差 α = ∑ i = 1 n ( x i − x ˉ ) 2 n \alpha=\dfrac{\sum\limits_{i=1}^{n}(x_i-\bar{x})^2}{n} α = n i = 1 ∑ n ( x i − x ˉ ) 2
分析得到 x ˉ = ∑ i = 1 n x i n \bar{x}=\dfrac{\sum\limits_{i=1}^nx_i}{n} x ˉ = n i = 1 ∑ n x i x i x_i x i x ˉ \bar{x} x ˉ ∑ i = 1 8 ∑ j = 1 8 w i , j n \dfrac{\sum\limits_{i=1}^8\sum\limits_{j=1}^8w_{i,j}}{n} n i = 1 ∑ 8 j = 1 ∑ 8 w i , j 其中 w i , j w_{i,j} w i , j 。
所以可以预处理 x ˉ \bar{x} x ˉ
此时可以发现将每个 x i x_i x i ( x i − x ˉ ) 2 n \dfrac{(x_i-\bar{x})^2}{n} n ( x i − x ˉ ) 2
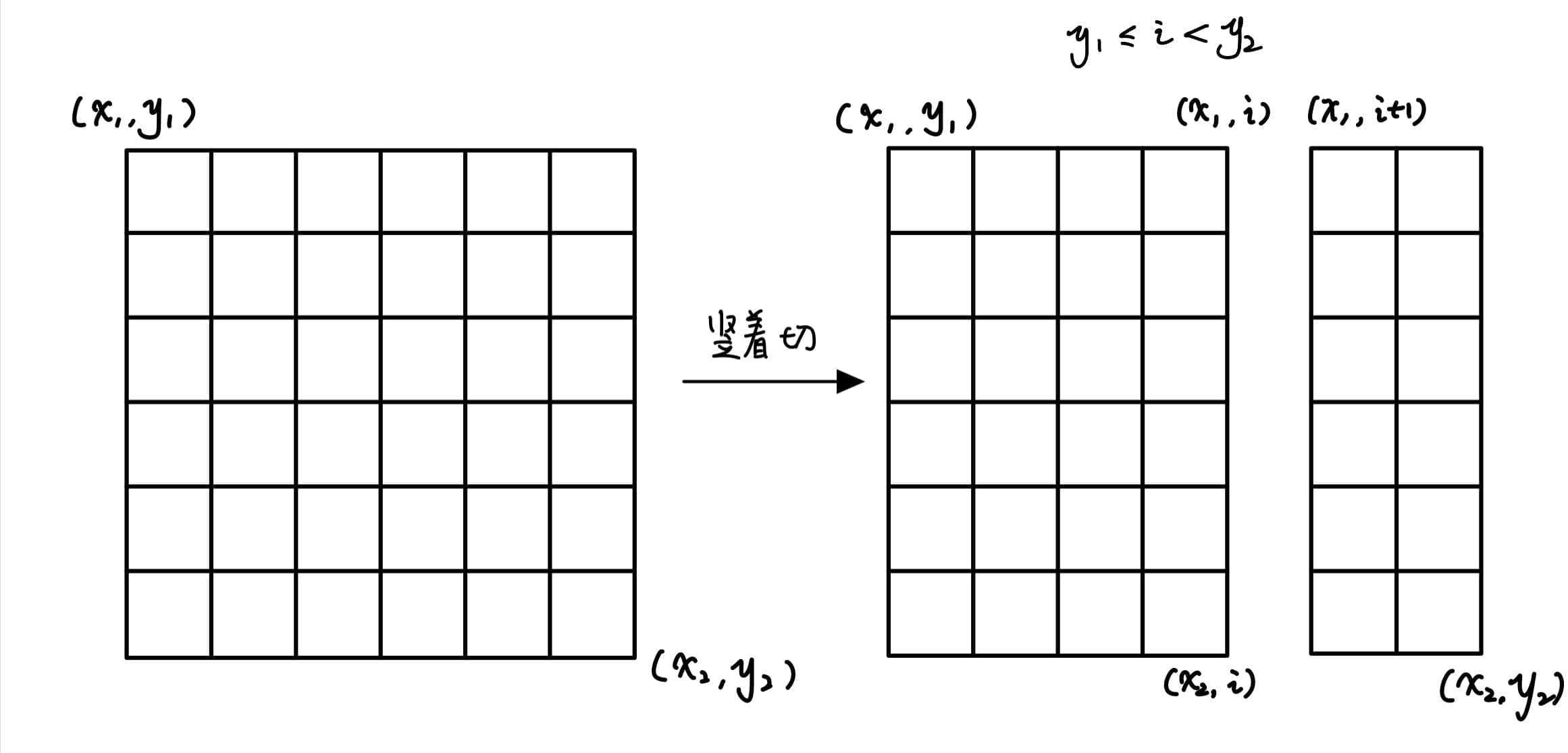
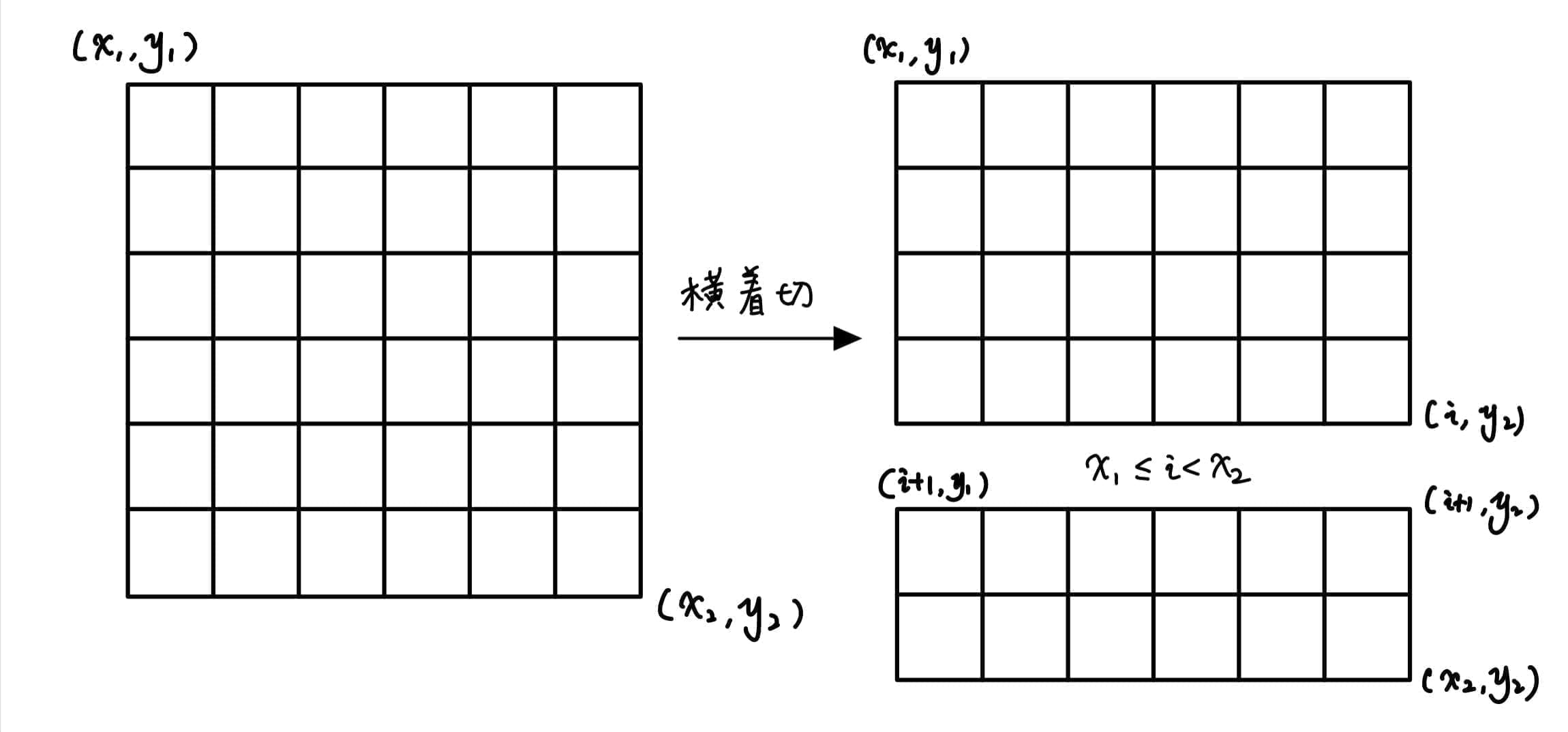
由于此题是一个比较明显的区间分割问题,考虑使用区间 DP。
令 f x 1 , y 1 , x 2 , y 2 , k f_{x_1,y_1,x_2,y_2,k} f x 1 , y 1 , x 2 , y 2 , k ( x 1 , y 1 ) ( x 2 , y 2 ) (x_1,y_1)(x_2,y_2) ( x 1 , y 1 ) ( x 2 , y 2 ) k k k 标准差 α \alpha α f 1 , 1 , 8 , 8 , n \sqrt{f_{1,1,8,8,n}} f 1 , 1 , 8 , 8 , n
边界 k = 1 k=1 k = 1 f x 1 , y 1 , x 2 , y 2 , k = ( ( ∑ i = x 1 x 2 ∑ j = y 1 y 2 w i , j ) − x ˉ ) 2 n f_{x_1,y_1,x_2,y_2,k}=\dfrac{((\sum\limits_{i=x_1}^{x_2}\sum\limits_{j=y_1}^{y_2}w_{i,j})-\bar{x})^2}{n} f x 1 , y 1 , x 2 , y 2 , k = n (( i = x 1 ∑ x 2 j = y 1 ∑ y 2 w i , j ) − x ˉ ) 2
在状态转移时,分类讨论水平切还是竖直切,枚举在哪里切,再分类讨论是要哪一块。
则可得出状态转移方程(详见代码)。
注意可用二维前缀和来维护子矩阵,从而 O ( 1 ) O(1) O ( 1 )
总时间复杂度 O ( 8 5 n ) O(8^5n) O ( 8 5 n )
由于循环太多,采用记忆化搜索写。
代码中 X 即为 x ˉ \bar{x} x ˉ get 函数是求 ( x i − x ˉ ) 2 n \dfrac{(x_i-\bar{x})^2}{n} n ( x i − x ˉ ) 2 s 即为二位前缀和数组。
再次强调 f x 1 , y 1 , x 2 , y 2 , k f_{x_1,y_1,x_2,y_2,k} f x 1 , y 1 , x 2 , y 2 , k ( x 1 , y 1 ) ( x 2 , y 2 ) (x_1,y_1)(x_2,y_2) ( x 1 , y 1 ) ( x 2 , y 2 ) k k k 标准差 α \alpha α 所以最后还要开根号!
Solution
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 #include <iostream> #include <cmath> #include <iomanip> #include <cstring> using namespace std;const int N = 10 , M = 20 ;int n;double f[N][N][N][N][M];double s[N][N];double X;double get (int x1, int y1, int x2, int y2) double sum = s[x2][y2] - s[x1 - 1 ][y2] - s[x2][y1 - 1 ] + s[x1 - 1 ][y1 - 1 ]; return (sum - X) * (sum - X) / n; } double dp (int x1, int y1, int x2, int y2, int k) double &v = f[x1][y1][x2][y2][k]; if (v >= 0 ) return v; if (k == 1 ) return v = get (x1, y1, x2, y2); v = 1e9 ; for (int i = x1; i < x2; ++i) { v = min (v, dp (x1, y1, i, y2, k - 1 ) + get (i + 1 , y1, x2, y2)); v = min (v, dp (i + 1 , y1, x2, y2, k - 1 ) + get (x1, y1, i, y2)); } for (int j = y1; j < y2; ++j) { v = min (v, dp (x1, y1, x2, j, k - 1 ) + get (x1, j + 1 , x2, y2)); v = min (v, dp (x1, j + 1 , x2, y2, k - 1 ) + get (x1, y1, x2, j)); } return v; } int main () cin >> n; for (int i = 1 ; i <= 8 ; ++i) { for (int j = 1 ; j <= 8 ; ++j) { cin >> s[i][j]; s[i][j] += s[i - 1 ][j] + s[i][j - 1 ] - s[i - 1 ][j - 1 ]; } } X = s[8 ][8 ] / n; memset (f, -1 , sizeof f); cout << fixed << setprecision (3 ) << sqrt (dp (1 , 1 , 8 , 8 , n)); }
题目描述
“多边形游戏”是一款单人益智游戏。
游戏开始时,给定玩家一个具有 N N N N N N 1 ∼ N 1 \sim N 1 ∼ N 1 1 1 N = 4 N = 4 N = 4
每个顶点上写有一个整数,每个边上标有一个运算符 +(加号)或运算符 *(乘号)。
第一步,玩家选择一条边,将它删除。
接下来在进行 N − 1 N-1 N − 1
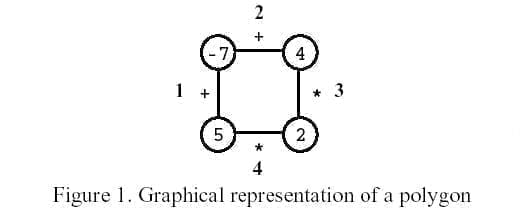
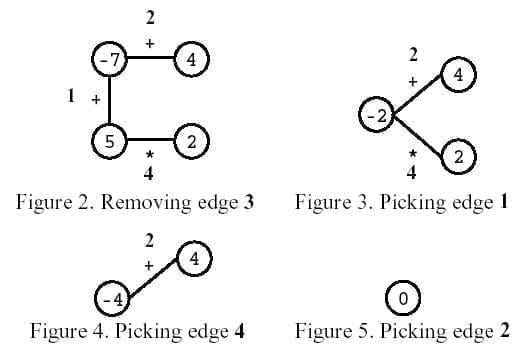
下面是用图 1 1 1
最终,游戏仅剩一个顶点,顶点上的数值就是玩家的得分,上图玩家得分为 0 0 0
请计算对于给定的 N N N
输入格式
输入包含两行,第一行为整数 N N N
第二行用来描述多边形所有边上的符号以及所有顶点上的整数,从编号为 1 1 1
其中描述顶点即为输入顶点上的整数,描述边即为输入边上的符号,其中加号用 t 表示,乘号用 x 表示。
输出格式
输出包含两行,第一行输出最高分数。
在第二行,将满足得到最高分数的情况下,所有的可以在第一步删除的边的编号从小到大输出,数据之间用空格隔开。
数据范围
3 ≤ N ≤ 50 3 \le N \le 50 3 ≤ N ≤ 50 [ − 32768 , 32767 ] [-32768,32767] [ − 32768 , 32767 ]
输入样例 :
输出样例 :
算法分析
Solution
题目描述
虽然探索金字塔是极其老套的剧情,但是有一队探险家还是到了某金字塔脚下。
经过多年的研究,科学家对这座金字塔的内部结构已经有所了解。
首先,金字塔由若干房间组成,房间之间连有通道。
如果把房间看作节点,通道看作边的话,整个金字塔呈现一个有根树结构,节点的子树之间有序,金字塔有唯一的一个入口通向树根。
并且,每个房间的墙壁都涂有若干种颜色的一种。
探险队员打算进一步了解金字塔的结构,为此,他们使用了一种特殊设计的机器人。
这种机器人会从入口进入金字塔,之后对金字塔进行深度优先遍历。
机器人每进入一个房间(无论是第一次进入还是返回),都会记录这个房间的颜色。
最后,机器人会从入口退出金字塔。
显然,机器人会访问每个房间至少一次,并且穿越每条通道恰好两次(两个方向各一次), 然后,机器人会得到一个颜色序列。
但是,探险队员发现这个颜色序列并不能唯一确定金字塔的结构。
现在他们想请你帮助他们计算,对于一个给定的颜色序列,有多少种可能的结构会得到这个序列。
因为结果可能会非常大,你只需要输出答案对1 0 9 10^9 1 0 9
输入格式
输入仅一行,包含一个字符串 S S S 300 300 300
输出格式
输出一个整数表示答案。
输入样例 :
输出样例 :
算法分析
Solution

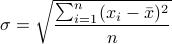 ,其中平均值
,其中平均值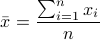 , 为第 块矩形棋盘的总分。
, 为第 块矩形棋盘的总分。