参考《算法竞赛进阶指南》 、AcWing题库
链表与邻接表
数组是一种支持随机访问, 但不支持在任意位置插入或删除元素的数据结构。与之相对应, 链表支持在任意位置插入或删除, 但只能按顺序依次访问其中的元素。我们可以用一个 struct 表示链表的节点, 其中可以存储任意数据。另外用 prev 和 next 两个指针指向前后相邻的两个节点, 构成一个常见的双向链表结构。为了避免在左右两端或者空链表中访问越界, 我们通常建立额外的两个节点 head 与 tail 代表链表头尾 , 把实际数据节点存储在 head 与 tail 之间, 来减少链表边界处的判断, 降低编程复杂度。
链表的正规形式一般通过动态分配内存、指针等实现, 为了避免内存泄露、方便调试, 使用数组模拟链表、下标模拟指针也是常见的做法。读者对于链表应该已经有所了解, 这里就不再赘述。两种实现形式的参考程序:
双向链表
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 struct Node { int value; Node *prev, *next; }; Node *head, *tail; void initialize () head = new Node (); tail = new Node (); head->next = tail; tail->prev = head; } void insert (Node *p, int value) auto q = new Node (); q->value = value; q->prev = p; q->next = p->next; p->next = q; q->next->prev = q; } void remove (Node *p) p->prev->next = p->next; p->next->prev = p->prev; delete p; } void recycle () while (head != tail) { head = head->next; delete head->prev; } delete tail; }
数组模拟链表
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 struct Node { int value; int prev, next; } node[SIZE]; int head, tail, tot;int initialize () tot = 2 ; head = 1 , tail = 2 ; node[head].next = tail; node[tail].prev = head; } int insert (int p, int value) auto q = ++tot; node[q].value = value; node[q].prev = p; node[q].next = node[p].next; node[p].next = q; node[node[q].next].prev = q; } void remove (int p) node[node[p].prev].next = node[p].next; node[node[p].next].prev = node[p].prev; } void clear () memset (node, 0 , sizeof head = tail = tot = 0 ; }
例题
给定一个长度为 n n n A A A A A A
对于 A A A A i A_i A i
min 1 ≤ j < i ∣ A i − A j ∣ \min_{1 \le j <i}|A_i-A_j| min 1 ≤ j < i ∣ A i − A j ∣
以及令上式取到最小值的 j j j P i P_i P i A j A_j A j
输入格式
第一行输入整数 n n n
第二行输入 n n n A 1 … A n A_1…A_n A 1 … A n
输出格式
输出共 n − 1 n-1 n − 1
分别表示当 i i i 2 ∼ n 2 \sim n 2 ∼ n min 1 ≤ j < i ∣ A i − A j ∣ \min_{1 \le j <i}|A_i-A_j| min 1 ≤ j < i ∣ A i − A j ∣ P i P_i P i
数据范围
n ≤ 1 0 5 n \le 10^5 n ≤ 1 0 5 ∣ A i ∣ ≤ 1 0 9 |A_i| \le 10^9 ∣ A i ∣ ≤ 1 0 9
输入样例:
输出样例:
算法分析
解法一: 平衡树 (STL set)
把 A 1 , A 2 , ⋯ , A n A_{1}, A_{2}, \cdots, A_{n} A 1 , A 2 , ⋯ , A n A i A_{i} A i 1 ≤ j < i 1 \leq j<i 1 ≤ j < i A j A_{j} A j A i A_{i} A i
若能维护一个有序集合, 则集合中与 A i A_{i} A i A i A_{i} A i A i A_{i} A i A i A_{i} A i
而二叉平衡树就是一个支持动态插入、查询前以及查询后继的数据结构。在 C++中, STL set 也为我们提供了这些功能。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 #include <set> #include <cstdio> #include <iostream> using namespace std;const int INF = 0x7f7f7f7f ;set<pair<int , int >> s; int main () int n, a; cin >> n >> a; s.insert (make_pair (a, 1 )); for (int i = 2 ; i <= n; i++) { scanf ("%d" , &a); s.insert (make_pair (a, i)); set<pair<int , int >>::iterator it = s.find (make_pair (a, i)); pair<int , int > ans; ans.first = INF; if (++it != s.end ()) ans = make_pair ((*it).first - a, (*it).second); it = s.find (make_pair (a, i)); if (it-- != s.begin () && ans.first >= a - (*it).first) ans = make_pair (a - (*it).first, (*it).second); cout << ans.first << " " << ans.second << endl; } return 0 ; }
解法二:双链表 + 存储指针
把序列 A A A B B B B i B_i B i A i A_i A i
因为链表有序, 所以在链表中, 指针 B n B_{n} B n p r e v prev p re v n e x t next n e x t A n A_n A n A n A_{n} A n A n A_{n} A n
接下来, 我们在链表中删除 B n B_{n} B n O ( 1 ) O(1) O ( 1 )
此时, 我们按同样方法考虑 B n − 1 B_{n-1} B n − 1 p r e v prev p re v n e x t next n e x t B n − 1 B_{n-1} B n − 1
依此类推, 最终即可求出与每个 A i A_{i} A i
两种解法的时间复杂度都是 O ( n log n ) O(n \log n) O ( n log n )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 #include <cstdio> #include <iostream> #include <algorithm> using namespace std;const int N = 100006 ;struct A { int a, w, prv, nxt; bool operator < (const A x) const { return a < x.a; } } a[N]; int n, b[N];struct ANS { int x, k; } ans[N]; int main () cin >> n; for (int i = 1 ; i <= n; i++) { scanf ("%d" , &a[i].a); a[i].w = i; } sort (a + 1 , a + n + 1 ); for (int i = 1 ; i <= n; i++) { b[a[i].w] = i; a[i].prv = i - 1 ; a[i].nxt = i + 1 ; } int l = 1 , r = n; for (int i = n; i > 1 ; i--) { if (b[i] == r) { ans[i].x = a[r].a - a[a[r].prv].a; ans[i].k = a[a[r].prv].w; r = a[r].prv; } else if (b[i] == l) { ans[i].x = a[a[l].nxt].a - a[l].a; ans[i].k = a[a[l].nxt].w; l = a[l].nxt; } else { ans[i].x = a[a[b[i]].nxt].a - a[b[i]].a; ans[i].k = a[a[b[i]].nxt].w; if (a[b[i]].a - a[a[b[i]].prv].a <= ans[i].x) { ans[i].x = a[b[i]].a - a[a[b[i]].prv].a; ans[i].k = a[a[b[i]].prv].w; } } a[a[b[i]].prv].nxt = a[b[i]].nxt; a[a[b[i]].nxt].prv = a[b[i]].prv; } for (int i = 2 ; i <= n; i++) printf ("%d %d\n" , ans[i].x, ans[i].k); return 0 ; }
Solution
依次读入一个整数序列,每当已经读入的整数个数为奇数时,输出已读入的整数构成的序列的中位数。
输入格式
第一行输入一个整数 P P P
每个数据集的第一行首先输入一个代表数据集的编号的整数。
然后输入一个整数 M M M M M M
数据集的剩余行由数据集的数据构成,每行包含 10 10 10 10 10 10
输出格式
对于每个数据集,第一行输出两个整数,分别代表数据集的编号以及输出中位数的个数(应为数据个数加一的二分之一),数据之间用空格隔开。
数据集的剩余行由输出的中位数构成,每行包含 10 10 10 10 10 10
输出中不应该存在空行。
数据范围
1 ≤ P ≤ 1000 1 \le P \le 1000 1 ≤ P ≤ 1000 1 ≤ M ≤ 99999 1 \le M \le 99999 1 ≤ M ≤ 99999 M M M 5 × 1 0 5 5 \times 10^5 5 × 1 0 5
输入样例:
1 2 3 4 5 6 7 8 9 3 1 9 1 2 3 4 5 6 7 8 9 2 9 9 8 7 6 5 4 3 2 1 3 23 23 41 13 22 -3 24 -31 -11 -8 -7 3 5 103 211 -311 -45 -67 -73 -81 -99 -33 24 56
输出样例:
1 2 3 4 5 6 7 1 5 1 2 3 4 5 2 5 9 8 7 6 5 3 12 23 23 22 22 13 3 5 5 3 -3 -7 -3
算法分析
在 排序 一文中, 我们讨论了本题的 “对顶堆” 做法。这里我们再介绍一种使用链表的离线做法。我们可以先把整个序列读入进来, 排序之后依次插入一个链表, 此时我们可以知道整个序列的中位数 P P P
与上一道题一样, 为了删除一个整数, 我们需要找到该整数在链表中对应的节点。 上一题建立了一个指针数组, 但是本题的整数范围较大, 需要用 Hash 表或者 STL map 记录这些指针。
每次删去一个整数 X X X P P P X X X P P P P P P
在上面两道例题中, 我们都用了 “倒序处理” 的方法, 利用链表容易执行 “删除” 操作的特性, 快速地找到了答案。
Solution
邻接表
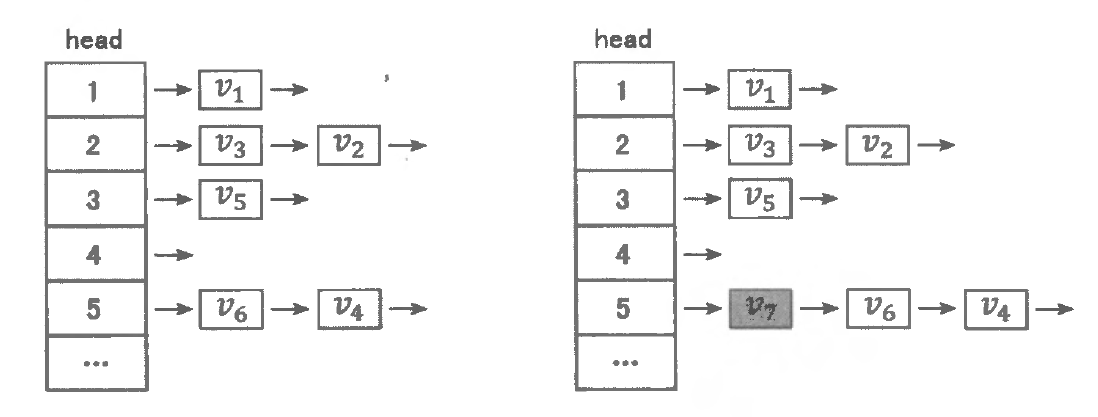
在与链表相关的诸多结构中, 邻接表是相当重要的一个。它是树与图结构的一般化存储方式, 还能用于实现我们开散列 Hash 表。实际上, 邻接表可以看成 “带有索引数组的多个数据链表” 构成的结构集合。在这样的结构中存储的数据被分成若干类, 每一类的数据构成一个链表。每一类还有一个代表元素, 称为该类对应链表的 “表头” 。所有 “表头” 构成一个表头数组, 作为一个可以随机访问的索引, 从而可以通过表头数组定位到某一类数据对应的链表。为了方便起见, 本书将这类结构统称为 “邻接表” 结构。
如下图左侧所示, 这是一个存储了 6 个数据节点 v 1 ∼ v 6 v_{1} \sim v_{6} v 1 ∼ v 6
当需要插入新的数据节点时, 我们可以通过表头数组 head 定位到新的数据节点所属类别的链表表头, 将新数据在表头位置插入。如下图右侧所示, 在邻接表中插入了属于第 5 类的新数据节点 v 7 v_{7} v 7
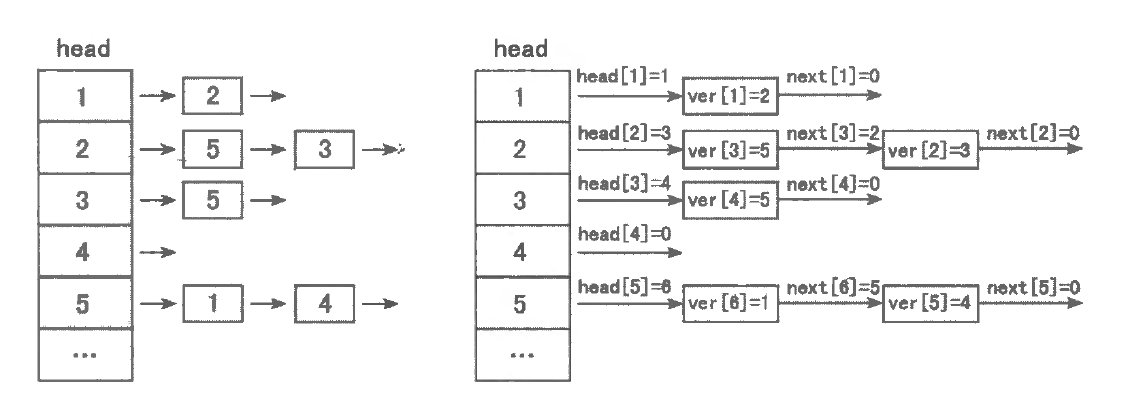
在一个具有 n n n m m m n n n x x x x x x [ x ] [x] [ x ] x x x x x x
上图是在邻接表中插入一张 5 个点、 6 条边的有向图之后的状态。这 6 条边按照插入的顺序依次是 ( 1 , 2 ) , ( 2 , 3 ) , ( 2 , 5 ) , ( 3 , 5 ) , ( 5 , 4 ) , ( 5 , 1 ) (1,2),(2,3),(2,5),(3,5),(5,4),(5,1) ( 1 , 2 ) , ( 2 , 3 ) , ( 2 , 5 ) , ( 3 , 5 ) , ( 5 , 4 ) , ( 5 , 1 )
1 2 3 4 5 6 7 8 9 10 11 void add (int x, int y, int z) ver[++tot] = y, edge[tot] = z; next[tot] = head[x], head[x] = tot; } for (int i = head[x]; i; i = next[i]) { int y = ver[i], z = edge[i]; }
上面的代码片段用数组模拟链表的方式存储了一张带权有向图的邻接表结构。
对于无向图, 我们把每条无向边看作两条有向边插入即可。有一个小技巧是, 结合在位运算文中提到的 “成对变换” 的位运算性质, 我们可以在程序最开始时, 初始化变量 t o t = 1 t o t=1 t o t = 1 ⋯ \cdots ⋯ [ i ] [i] [ i ] i i i [ i [i [ i ] ] ] i i i
1 2 3 4 5 6 7 8 9 10 int h[N], to[M], w[M], ne[M], idx;void add (int x , int y, int z) to[idx] = y, w[idx] = z, ne[idx] = h[x], h[x] = idx++; } void init () memset (h, -1 , sizeof h); idx = 0 ; }