参考《算法竞赛进阶指南》、AcWing题库

栈

栈是一种 “后进先出” 的线性数据结构。栈只有一端能够进出元素, 我们一般称这一端为栈顶, 另一端为栈底。添加或删除栈中元素时, 我们只能将其插入到栈顶 (进栈), 或者把栈顶元素从栈中取出 (出栈)。
我们可以在 C++中用一个数组和一个变量 (记录栈顶位置) 来实现栈结构。在之前的章节我们也提到过, 栈是机器实现递归 (深度优先搜索) 的基本结构。

41. 包含min函数的栈 - AcWing题库

题目描述

设计一个支持push，pop，top等操作并且可以在O(1)时间内检索出最小元素的堆栈。

push(x)–将元素x插入栈中
pop()–移除栈顶元素
top()–得到栈顶元素
getMin()–得到栈中最小元素

样例

MinStack minStack = new MinStack();
minStack.push(-1);
minStack.push(3);
minStack.push(-4);
minStack.getMin();   --> Returns -4.
minStack.pop();
minStack.top();      --> Returns 3.
minStack.getMin();   --> Returns -1.

算法分析

栈结构原本就支持 $O(1)$ 的入栈、出栈操作, 但不支持查询最小值的操作。一个比较直接的思路是, 我们知道二叉堆是一种支持插入、取出堆顶、查询最值的数据结构, 如果在维护一个栈的同时再维护一个存储同样元素的二叉堆, 就可以支持题目中要求的操作。然而, 它的时间复杂度是 $O(\log N)$ 。如果我们只用一个变量记录最小值, 当发生出栈操作时, 如果最小值恰好被出栈, 就无法得知新的最小值是什么。这启发我们使用一个线性结构来保存历史上每个时刻的最小值, 这样就可以在出栈后进行还原。

我们建立两个栈, 栈 $A$ 存储原本的数据, 栈 $B$ 存储栈 $A$ 中以栈底开头的每段数据的最小值, 就像下面这样:

A: $\begin{array}{llllll}9 & 2 & 1 & 5 & 3 & 0 & \end{array}$
B: $\begin{array}{llllllll}9 & 2 & 1 & 1 & 1 & 0 & 0\end{array}$

当执行 Push $(x)$ 操作时, 在 $A$ 中插入 $x$ , 在 $B$ 中插入 $\min (B$ 的栈顶数据, $x)$ 。在执行 Pop 操作时, 在 $A 、 B$ 中分别弹出栈顶。在执行 GetMin 操作时, 直接输出 $B$ 的栈顶数据。每个操作的时间复杂度都是 $O(1)$ 。

Solution

128. 编辑器

题目描述

你将要实现一个功能强大的整数序列编辑器。

在开始时，序列是空的。

编辑器共有五种指令，如下：

1、I x，在光标处插入数值 $x$ 。
2、D，将光标前面的第一个元素删除，如果前面没有元素，则忽略此操作。
3、L，将光标向左移动，跳过一个元素，如果左边没有元素，则忽略此操作。
4、R，将光标向右移动，跳过一个元素，如果右边没有元素，则忽略次操作。
5、Q k，假设此刻光标之前的序列为 $a_1,a_2,…,a_n$ ，输出 $max_{1 \le i \le k}S_i$ ，其中 $S_i=a_1+a_2+…+a_i$ 。

输入格式

第一行包含一个整数 $Q$ ，表示指令的总数。

接下来 $Q$ 行，每行一个指令，具体指令格式如题目描述。

输出格式

每一个 Q k 指令，输出一个整数作为结果，每个结果占一行。

数据范围

$1 \le Q \le 10^6$ ,
$|x| \le 10^3$ ,
$1 \le k \le n$

输入样例：

8
I 2
I -1
I 1
Q 3
L
D
R
Q 2

输出样例：

1
2

2
3

样例解释

算法分析

本题的特殊点在于, $I, D, L, R$ 四种操作都在光标位置处发生, 并且操作完成后光标至多移动 1 个位置。根据这种 “始终在序列中间某个指定位置进行修改” 的性质, 再联想到我们动态维护中位数的 “对顶堆” 算法, 我们不难想到一个类似的 “对顶栈” 做法。

建立两个栈, 栈 $A$ 存储从序列开头到当前光标位置的这一段子序列, 栈 $B$ 存储从当前光标位置到序列结尾的这一段子序列, 二者都以光标所在的那一端作为栈顶。这两个栈合起来就保存了整个序列。因为查询操作的 $k$ 不超过光标位置, 所以我们用一个数组 $f$ 维护栈 $A$ 的前缀和的最大值即可。设 $A$ 的栈顶位置下标是 $p_{A}$ , $sum$ 是序列 $A$ 的前缀和数组。

对于 $I \; x$ 操作;

把 $x$ 插入栈 $A$ ;
更新 $\operatorname{sum}\left[p_{A}\right]=\operatorname{sum}\left[p_{A}-1\right]+A\left[p_{A}\right]$ ;
更新 $f\left[p_{A}\right]=\max \left(f\left[p_{A}-1\right], \operatorname{sum}\left[p_{A}\right]\right)$ 。

对于 $D$ 操作, 把 $A$ 的栈顶出栈。

对于 $\mathrm{L}$ 操作, 弹出 $A$ 的栈顶, 插入到 $B$ 中。

对于 $R$ 操作:

弹出 $\mathrm{B}$ 的栈顶, 插入到 $\mathrm{A}$ 中;
更新 $\operatorname{sum}\left[p_{A}\right]=\operatorname{sum}\left[p_{A}-1\right]+A\left[p_{A}\right]$ ;
更新 $f\left[p_{A}\right]=\max \left(f\left[p_{A}-1\right], \operatorname{sum}\left[p_{A}\right]\right) 。$

对于 $\mathrm{Q} \;k$ 询问, 直接返回 $f[k]$ 。

通过这样两个 “对顶栈”, 我们在 $O(1)$ 的时间内实现了每种操作和询问。

Solution

进出栈序列问题

给定 $1 \sim N$ 这 $N$ 个整数和一个无限大的栈, 每个数都要进栈并出栈一次。如果进栈的顺序为 $1,2, \cdots, N$ , 那么可能的出栈序列有多少种?

方法一: 搜索 (枚举/递归), $O\left(2^{N}\right)$

一个很直观的想法是, 面对任何一个状态我们只有两种选择:

把下一个数进栈。
把当前栈顶的数出栈 (如果栈非空)。

根据上一章学到的知识, 我们可以枚举每一步如何选择, 用递归实现这个规模为 $\mathrm{O}\left(2^{N}\right)$ 的枚举, 这样就得到了所有可能的出栈序列方案。

方法二: 递推, $O\left(N^{2}\right)$

本题只要求我们计算出可能出栈序列有多少种, 并不关心具体方案, 于是我们可以使用递推直接进行统计。设 $S_{N}$ 表示进栈顺序为 $1,2, \cdots, N$ 时可能的出栈序列总数。根据递推的理论, 我们需要想办法把问题分解成若干个类似的子问题。

考虑 “1” 这个数排在最终出栈序列中的位置, 如果最后 “ 1 ” 这个数排在第 $k$ 个, 那么整个序列的进出栈过程就是:

整数 1 入栈。
整数 $2 \sim k$ 这 $k-1$ 个数按某种顺序进出栈。
整数 1 出栈, 排在第 $k$ 个。
整数 $k+1 \sim N$ 这 $N-k$ 个数按某种顺序进出栈。

于是整个问题就被 “ 1 " 这个数划分成了 “ $k-1$ 个数进出栈” 和 “ $N-k$ 个数进出栈” 这两个子问题, 得到递推公式:

$S_{N}=\sum_{k=1}^{N} S_{k-1} * S_{N-k}$

方法三: 动态规划, $O\left(N^{2}\right)$

在任何一个时刻, 我们实际上只关心有多少个数尚末入栈、有多少个数还在栈里, 并做出一步合法的操作, 并不关心这些数具体是哪些。因此, 我们可以用 $F[i, j]$ 表示有 $i$ 个数尚未进栈, 目前有 $j$ 个数在栈里, 已经有 $n-i-j$ 个数出栈时的方案总数。

在最终状态下, 即所有数已经出栈时, 顺序已经确定, 所以边界为: $F[0,0]=1$ 。

我们需要求出初始状态下, 即所有数尚未进栈时, 可以到达上述边界的方案总数, 所以目标为: $F[N, 0]$ 。

每一步的两种决策分别是 “把一个数进栈” 和 “把栈顶的数出栈”, 所以有公式:

$F[i, j]=F[i-1, j+1]+F[i, j-1]$

方法四: 数学, $\mathrm{O}(N)$

该问题等价于求第 $N$ 项 Catalan 数, 即 $C_{2 N}^{N} /(N+1)$ 。

129. 火车进栈

题目描述

这里有 $n$ 列火车将要进站再出站，但是，每列火车只有 $1$ 节，那就是车头。

这 $n$ 列火车按 $1$ 到 $n$ 的顺序从东方左转进站，这个车站是南北方向的，它虽然无限长，只可惜是一个死胡同，而且站台只有一条股道，火车只能倒着从西方出去，而且每列火车必须进站，先进后出。

也就是说这个火车站其实就相当于一个栈，每次可以让右侧头火车进栈，或者让栈顶火车出站。

车站示意如图：

出站<——    <——进站
       |车|
       |站|
       |__|

现在请你按《字典序》输出前 $20$ 种可能的出栈方案。

输入格式

输入一个整数 $n$ ，代表火车数量。

输出格式

按照《字典序》输出前 $20$ 种答案，每行一种，不要空格。

数据范围

$1 \le n \le 20$

输入样例：

输出样例：

算法分析

Solution

130. 火车进出栈问题

题目描述

一列火车 $n$ 节车厢，依次编号为 $1,2,3,…,n$ 。

每节车厢有两种运动方式，进栈与出栈，问 $n$ 节车厢出栈的可能排列方式有多少种。

输入格式

输入一个整数 $n$ ，代表火车的车厢数。

输出格式

输出一个整数 $s$ 表示 $n$ 节车厢出栈的可能排列方式数量。

数据范围

$1 \le n \le 60000$

输入样例：

输出样例：

算法分析

Solution

表达式计算

栈的一大用处是做算术表达式的计算。算术表达式通常有前缀、中缀、后缀三种表示方法。

中缀表达式, 是我们最常见的表达式, 例如: $3 *(1-2)$ 。

前缀表达式, 又称波兰式, 形如 “op $A B$ ”, 其中 op 是一个运算符, $A, B$ 是另外两个前缀表达式。例如: * 3-12。

后缀表达式, 又称逆波兰式, 形如 “ $A B$ op", 例如: $12-3 *$ 。

前缀和后缀表达式的值的定义是, 先递归求出 $A, B$ 的值, 二者再做 op 运算的结果。这两种表达式不需要使用括号, 其运算方案是唯一确定的。对于计算机来讲, 它最容易理解后缀表达式, 我们可以使用栈来 $\mathrm{O}(N)$ 地求出它的值。

后缀表达式求值

建立一个用于存数的栈, 逐一扫描该后缀表达式中的元素。
(1) 如果遇到一个数, 则把该数入栈。
(2) 如果遇到运算符, 就取出栈顶的两个数进行计算, 把结果入栈。
扫描完成后, 栈中恰好剩下一个数, 就是该后缀表达式的值。

读者可以模拟 $12-3 *$ 这个后缀表达式的计算过程进行体会。

如果想让计算机求解我们人类常用的中缀表达式的值, 最快的办法就是把中缀表达式转化成后缀表达式, 再使用上述方法求值。这个转化过程同样可以使用栈来 $O(N)$ 地完成。

中缀表达式转后缀表达式

建立一个用于存运算符的栈, 逐一扫描该中缀表达式中的元素。
(1) 如果遇到一个数, 输出该数。
(2) 如果遇到左括号, 把左括号入栈。
(3) 如果遇到右括号, 不断取出栈顶并输出, 直到栈顶为左括号, 然后把左括号出栈。
(4) 如果遇到运算符, 只要栈顶符号的优先级不低于新符号, 就不断取出栈顶并输出, 最后把新符号进栈。优先级为乘除 $>$ 加减 $>$ 左括号。
依次取出并输出栈中的所有剩余符号, 最终输出的序列就是一个与原中缀表达式等价的后缀表达式。

读者可以写一些稍微复杂的中缀表达式进行模拟, 体会这个计算过程。

以上例子中包含的都是一位数, 如果是多位数, 并且表达式是使用字符串逐字符存储的, 我们只需要稍加判断, 把连续的一段数字看成一个数即可。

当然, 我们也可以不转化成后缀表达式, 而是使用递归法直接求解中缀表达式的值, 时间复杂度为 $\mathrm{O}\left(N^{2}\right)$ 。

中缀表达式的递归法求值

目标: 求解中缀表达式 $S[1 \sim N]$ 的值。

子问题: 求解中缀表达式 $S$ 的子区间表达式 $S[L \sim R]$ 的值。

在 $L \sim R$ 中考虑没有被任何括号包含的运算符:
(1) 若存在加减号, 选其中最后一个, 分成左右两半递归, 结果相加减, 返回。
(2) 若存在乘除号, 选其中最后一个, 分成左右两半递归, 结果相乘除, 返回。
若不存在没有被任何括号包含的运算符:
(1) 若首尾字符是括号, 递归求解 $S[L+1 \sim R-1]$ , 把结果返回。
(2) 否则, 说明区间 $S[L \sim R]$ 是一个数, 直接返回数值。

单调栈

131. 直方图中最大的矩形

题目描述

直方图是由在公共基线处对齐的一系列矩形组成的多边形。

矩形具有相等的宽度，但可以具有不同的高度。

例如，图例左侧显示了由高度为 $2,1,4,5,1,3,3$ 的矩形组成的直方图，矩形的宽度都为 $1$ ：

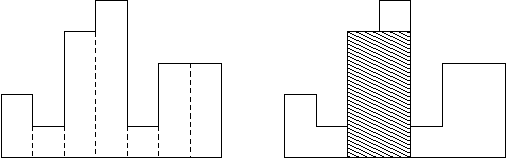
通常，直方图用于表示离散分布，例如，文本中字符的频率。

现在，请你计算在公共基线处对齐的直方图中最大矩形的面积。

图例右图显示了所描绘直方图的最大对齐矩形。

输入格式

输入包含几个测试用例。

每个测试用例占据一行，用以描述一个直方图，并以整数 $n$ 开始，表示组成直方图的矩形数目。

然后跟随 $n$ 个整数 $h_1，…，h_n$ 。

这些数字以从左到右的顺序表示直方图的各个矩形的高度。

每个矩形的宽度为 $1$ 。

同行数字用空格隔开。

当输入用例为 $n=0$ 时，结束输入，且该用例不用考虑。

输出格式

对于每一个测试用例，输出一个整数，代表指定直方图中最大矩形的区域面积。

每个数据占一行。

请注意，此矩形必须在公共基线处对齐。

数据范围

$1 \le n \le 100000$ ,
$0 \le h_i \le 1000000000$

输入样例：

1
2
3

7 2 1 4 5 1 3 3
4 1000 1000 1000 1000
0

输出样例：

1
2

8
4000

算法分析

我们先来思考这样一个问题: 如果矩形的高度从左到右单调递增, 那么答案是多少? 显而易见, 我们可以尝试以每个矩形的高度作为最终矩形的高度, 并把宽度延伸到右边界, 得到一个矩形, 在所有这样的矩形面积中取最大值就是答案。如下图所示:

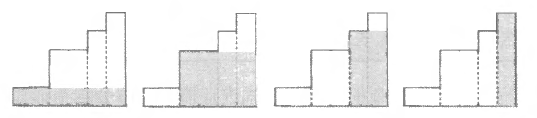
如果下一个矩形的高度比上一个小, 那么该矩形想利用之前的矩形一起构成一块较大的面积时, 这块面积的高度就不可能超过该矩形自己的高度。换句话说, 在考虑完上图中的四种情况后, 下图中打叉的那部分形状就没有丝毫用处了。

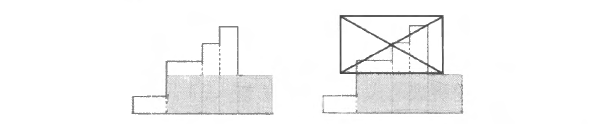
既然没有用处, 为什么不把这些比该矩形高的矩形都删掉, 用一个宽度累加、高度为该矩形自己的高度的新矩形 (就是上图中的阴影部分) 代替呢? 这样并不会对后续的计算产生影响。于是我们维护的轮廓就变成了一个高度始终单调递增的矩形序列, 问题变得可解了。

详细地说, 我们建立一个栈, 用来保存若干个矩形, 这些矩形的高度是单调递增的。我们从左到右依次扫描每个矩形:

如果当前矩形比栈顶矩形高, 直接进栈。

否则不断取出栈顶, 直至栈为空或者栈顶矩形的高度比当前矩形小。在出栈过程中, 我们累计被弹出的矩形的宽度之和, 并且每弹出一个矩形, 就用它的高度乘上累计的宽度去更新答案。整个出栈过程结束后, 我们把一个高度为当前矩形高度、宽度为累计值的新矩形入栈。

整个扫描结束后, 我们把栈中剩余的矩形依次弹出, 按照与上面相同的方法更新答案。为了简化程序实现, 也可以增加一个高度为 0 的矩形 $a[n+1]$ , 以避免在扫描结束后栈中有剩余矩形。

a[n + 1] = p = 0;
for (int i = 1; i <= n + 1; i++) {
	if (a[i] > s[p]) {
		s[++p] = a[i], w[p] = 1;
	} else {
		int width=0;
		while (s[p] > a[i]) {
			width += w[p];
			ans = max(ans, (long long)width * s[p]);
			p--;
		}
		s[++p] = a[i], w[p] = width + 1;
	}
}