线性DP

参考《算法竞赛进阶指南》、AcWing题库

具有线性”阶段“划分的动态规划算法被统称为线性DP。读者对于最长上升子序列(LIS)、最长公共子序列(LCS)、数字三角形(IOI1994)等DP的经典入门例题应该并不陌生，在动态规划的入门书籍或者网络上很容易找到这些问题的描述和解答。这里不会花费时间再次详细解释这些问题，但本着见微知著的思想，我们可以简单回顾它们，并尝试分析一下DP要素在其中的体现。

线性DP: 即线性动态规划，在本节中是一个作常广义的概念，不局限于“线性时间复杂度”的一维动态规划。与数学中的“线性空间”类似，如果一个动态规划算法的“状态”包含多个维度，但在每个维度上都具有“线性”变化的“阶段”，那么该动态规划算法同样称为“线性DP” 。

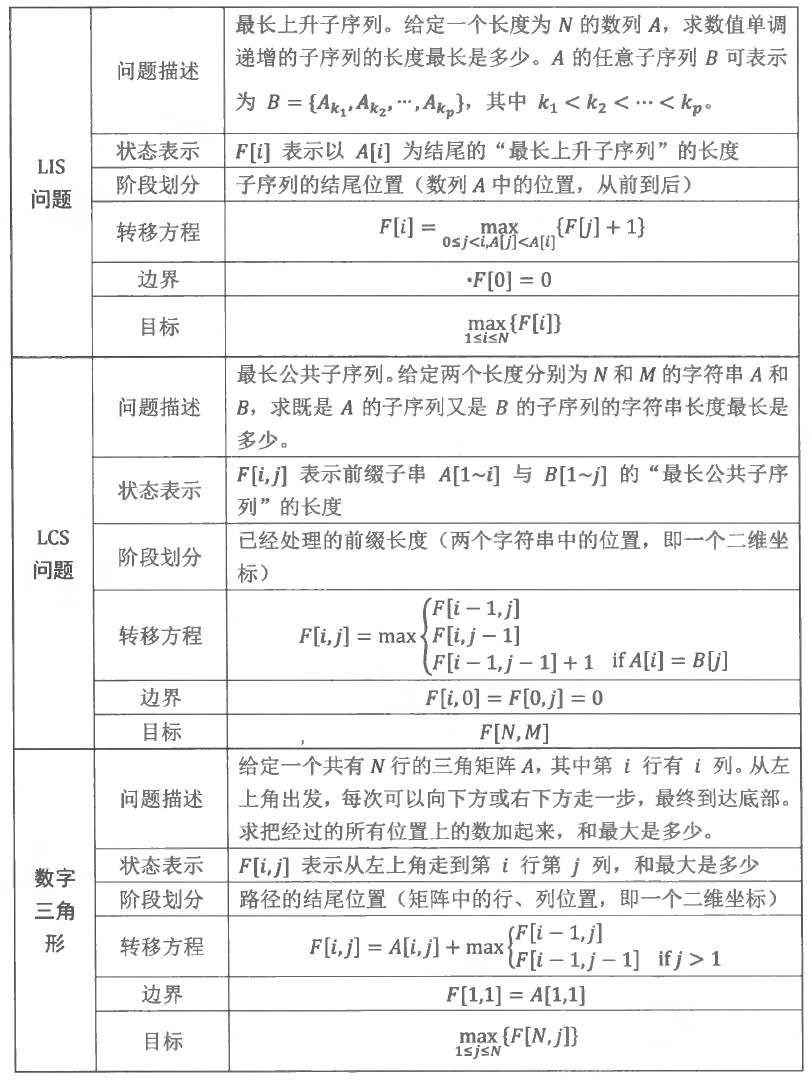
容易发现，无论状态表示是一维还是多维，DP算法在这些问题上都体现为“作用在线性空间上的递推”——DP的阶段沿着各个维度线性增长，从一个或多个“边界点”开始有方向地向整个状态空间转移、扩展，最后每个状态上都保留了以自身为“目标”的子问题的最优解。

这几个问题也是线性DP中最简单的一类，在这类问题中，需要计算的对象表现出明显的维度以及有序性，每个状态的求解直接构成一个阶段，这使得DP的状态表示就是阶段的表示。因此，我们只需要在每个维度上各取一个坐标值作为DP的状态，自然就可以描绘出“已求解部分”在状态空间中的轮廓特征，该轮廓的进展就是阶段的推移。另外，每个状态的求解显然只与之前阶段的最优解有关，最优子结构性质也得以验证。接下来，我们按顺序依次循环每个维度，根据问题要求递推求解的具体实现过程也就顺理成章了。

271. 杨老师的照相排列

题目描述

有 $N$ 个学生合影，站成左端对齐的 $k$ 排，每排分别有 $N_1, N_2, …, N_k$ 个人。 ( $N_1 \ge N_2 \ge … \ge N_k$ )

第 $1$ 排站在最后边，第 $k$ 排站在最前边。

学生的身高互不相同，把他们从高到底依次标记为 $1, 2, …, N$ 。

在合影时要求每一排从左到右身高递减，每一列从后到前身高也递减。

问一共有多少种安排合影位置的方案？

下面的一排三角矩阵给出了当 $N=6, k=3,N_1=3,N_2=2,N_3=1$ 时的全部 $16$ 种合影方案。注意身高最高的是 $1$ ，最低的是 $6$ 。

1
2
3

123 123 124 124 125 125 126 126 134 134 135 135 136 136 145 146
45  46  35  36  34  36  34  35  25  26  24  26  24  25  26  25
6   5   6   5   6   4   5   4   6   5   6   4   5   4   3   3

输入格式

输入包含多组测试数据。

每组数据两行，第一行包含一个整数 $k$ 表示总排数。

第二行包含 $k$ 个整数，表示从后向前每排的具体人数。

当输入 $k=0$ 的数据时，表示输入终止，且该数据无需处理。

输出格式

每组测试数据输出一个答案，表示不同安排的数量。

每个答案占一行。

数据范围

$1 \le k \le 5$ ,学生总人数不超过 $30$ 人。

输入样例：

输出样例：

算法分析

Solution

272. 最长公共上升子序列

题目描述

熊大妈的奶牛在小沐沐的熏陶下开始研究信息题目。

小沐沐先让奶牛研究了最长上升子序列，再让他们研究了最长公共子序列，现在又让他们研究最长公共上升子序列了。

小沐沐说，对于两个数列 $A$ 和 $B$ ，如果它们都包含一段位置不一定连续的数，且数值是严格递增的，那么称这一段数是两个数列的公共上升子序列，而所有的公共上升子序列中最长的就是最长公共上升子序列了。

奶牛半懂不懂，小沐沐要你来告诉奶牛什么是最长公共上升子序列。

不过，只要告诉奶牛它的长度就可以了。

数列 $A$ 和 $B$ 的长度均不超过 $3000$ 。

输入格式

第一行包含一个整数 $N$ ，表示数列 $A，B$ 的长度。

第二行包含 $N$ 个整数，表示数列 $A$ 。

第三行包含 $N$ 个整数，表示数列 $B$ 。

输出格式

输出一个整数，表示最长公共上升子序列的长度。

数据范围

$1 \le N \le 3000$ ,序列中的数字均不超过 $2^{31}-1$ 。

输入样例：

1
2
3

4
2 2 1 3
2 1 2 3

输出样例：

算法分析

Solution

273. 分级

题目描述

给定长度为 $N$ 的序列 $A$ ，构造一个长度为 $N$ 的序列 $B$ ，满足：

$B$ 非严格单调，即 $B_1 \le B_2 \le … \le B_N$ 或 $B_1 \ge B_2 \ge … \ge B_N$ 。
最小化 $S = \sum_{i=1}^N|A_i-B_i|$ 。

只需要求出这个最小值 $S$ 。

输入格式

第一行包含一个整数 $N$ 。

接下来 $N$ 行，每行包含一个整数 $A_i$ 。

输出格式

输出一个整数，表示最小 $S$ 值。

数据范围

$1 \le N \le 2000$ ,
$0 \le A_i \le 10^6$

输入样例：

输出样例：

算法分析

Solution

274. 移动服务

题目描述

一个公司有三个移动服务员，最初分别在位置 $1，2，3$ 处。

如果某个位置（用一个整数表示）有一个请求，那么公司必须指派某名员工赶到那个地方去。

某一时刻只有一个员工能移动，且不允许在同样的位置出现两个员工。

从 $p$ 到 $q$ 移动一个员工，需要花费 $c(p,q)$ 。

这个函数不一定对称，但保证 $c(p,p)=0$ 。

给出 $N$ 个请求，请求发生的位置分别为 $p_1 \sim p_N$ 。

公司必须按顺序依次满足所有请求，且过程中不能去其他额外的位置，目标是最小化公司花费，请你帮忙计算这个最小花费。

输入格式

第 $1$ 行有两个整数 $L,N$ ，其中 $L$ 是位置数量， $N$ 是请求数量，每个位置从 $1$ 到 $L$ 编号。

第 $2$ 至 $L+1$ 行每行包含 $L$ 个非负整数，第 $i+1$ 行的第 $j$ 个数表示 $c(i,j)$ ，并且它小于 $2000$ 。

最后一行包含 $N$ 个整数，是请求列表。

一开始三个服务员分别在位置 $1，2，3$ 。

输出格式

输出一个整数 $M$ ，表示最小花费。

数据范围

$3 \le L \le 200$ ,
$1 \le N \le 1000$

输入样例：

5 9
0 1 1 1 1
1 0 2 3 2
1 1 0 4 1
2 1 5 0 1
4 2 3 4 0
4 2 4 1 5 4 3 2 1

输出样例：

算法分析

Solution

275. 传纸条

题目描述

小渊和小轩是好朋友也是同班同学，他们在一起总有谈不完的话题。

一次素质拓展活动中，班上同学安排坐成一个 $m$ 行 $n$ 列的矩阵，而小渊和小轩被安排在矩阵对角线的两端，因此，他们就无法直接交谈了。

幸运的是，他们可以通过传纸条来进行交流。

纸条要经由许多同学传到对方手里，小渊坐在矩阵的左上角，坐标 $(1,1)$ ，小轩坐在矩阵的右下角，坐标 $(m,n)$ 。

从小渊传到小轩的纸条只可以向下或者向右传递，从小轩传给小渊的纸条只可以向上或者向左传递。

在活动进行中，小渊希望给小轩传递一张纸条，同时希望小轩给他回复。

班里每个同学都可以帮他们传递，但只会帮他们一次，也就是说如果此人在小渊递给小轩纸条的时候帮忙，那么在小轩递给小渊的时候就不会再帮忙，反之亦然。

还有一件事情需要注意，全班每个同学愿意帮忙的好感度有高有低（注意：小渊和小轩的好心程度没有定义，输入时用 $0$ 表示），可以用一个 $0 \sim 100$ 的自然数来表示，数越大表示越好心。

小渊和小轩希望尽可能找好心程度高的同学来帮忙传纸条，即找到来回两条传递路径，使得这两条路径上同学的好心程度之和最大。

现在，请你帮助小渊和小轩找到这样的两条路径。

输入格式

第一行有 $2$ 个用空格隔开的整数 $m$ 和 $n$ ，表示学生矩阵有 $m$ 行 $n$ 列。

接下来的 $m$ 行是一个 $m \times n$ 的矩阵，矩阵中第 $i$ 行 $j$ 列的整数表示坐在第 $i$ 行 $j$ 列的学生的好心程度，每行的 $n$ 个整数之间用空格隔开。

输出格式

输出一个整数，表示来回两条路上参与传递纸条的学生的好心程度之和的最大值。

数据范围

$1 \le n,m \le 50$

输入样例：

输出样例：

算法分析

Solution

276. I-区域

题目描述

在 $N \times M$ 的矩阵中，每个格子有一个权值，要求寻找一个包含 $K$ 个格子的凸连通块（连通块中间没有空缺，并且轮廓是凸的），使这个连通块中的格子的权值和最大。

注意：凸连通块是指：连续的若干行，每行的左端点列号先递减、后递增，右端点列号先递增、后递减。

求出这个最大的权值和，并给出连通块的具体方案，输出任意一种方案即可。

输入格式

第一行包含三个整数 $N,M$ 和 $K$ 。

接下来 $N$ 行每行 $M$ 个整数，表示 $N \times M$ 的矩阵上每个格子的权值（均不超过 $1000$ ）。

输出格式

第一行输出 Oil : X，其中 $X$ 为最大权值和。

接下来 $K$ 行每行两个整数 $x_i$ 和 $y_i$ ，用来描述所有格子的具体位置，每个格子位于第 $x_i$ 行，第 $y_i$ 列。

数据范围

$1 \le N,M \le 15$ ,
$0 \le K \le N \times M$

输入样例：

1
2
3

2 3 4 
10 20 30 
40 2 3

输出样例：

算法分析

Solution

277. 饼干

题目描述

圣诞老人共有 $M$ 个饼干，准备全部分给 $N$ 个孩子。

每个孩子有一个贪婪度，第 $i$ 个孩子的贪婪度为 $g[i]$ 。

如果有 $a[i]$ 个孩子拿到的饼干数比第 $i$ 个孩子多，那么第 $i$ 个孩子会产生 $g[i] \times a[i]$ 的怨气。

给定 $N、M$ 和序列 $g$ ，圣诞老人请你帮他安排一种分配方式，使得每个孩子至少分到一块饼干，并且所有孩子的怨气总和最小。

输入格式

第一行包含两个整数 $N,M$ 。

第二行包含 $N$ 个整数表示 $g_1 \sim g_N$ 。

输出格式

第一行一个整数表示最小怨气总和。

第二行 $N$ 个空格隔开的整数表示每个孩子分到的饼干数，若有多种方案，输出任意一种均可。

数据范围

$1 \le N \le 30$ ,
$N \le M \le 5000$ ,
$1 \le g_i \le 10^7$

输入样例：

1 2	3 20 1 2 3

输出样例：

1
2

2
2 9 9