前缀和与差分 | 算法基础

前缀和

前缀和是一种重要的预处理，能大大降低查询的时间复杂度。可以简单理解为“数列的前 $n$ 项的和”。

C++ 标准库中实现了前缀和函数 std::partial_sum，定义于头文件 <numeric> 中。

例题

有 $N$ 个的正整数放到数组 $A$ 里，现在要求一个新的数组 $B$，新数组的第 $i$ 个数 $B[i]$ 是原数组 $A$ 第 $0$ 到第 $i$ 个数的和。

输入

5
1 2 3 4 5

输出：

1 3 6 10 15

解题思路

递推：B[0] = A[0]，对于 $i \ge 1$ 则 B[i] = B[i-1] + A[i]。

参考代码

#include <iostream>
using namespace std;

int N, A[10000], B[10000];
int main() {
  cin >> N;
  for (int i = 0; i < N; i++) {
    cin >> A[i];
  }

  // 前缀和数组的第一项和原数组的第一项是相等的。
  B[0] = A[0];

  for (int i = 1; i < N; i++) {
    // 前缀和数组的第 i 项 = 原数组的 0 到 i-1 项的和 + 原数组的第 i 项。
    B[i] = B[i - 1] + A[i];
  }

  for (int i = 0; i < N; i++) {
    cout << B[i] << " ";
  }

  return 0;
}

二维/多维前缀和

多维前缀和的普通求解方法几乎都是基于容斥原理。

示例：一维前缀和扩展到二维前缀和

比如我们有这样一个矩阵 $a$，可以视为二维数组：

1 2 4 3
5 1 2 4
6 3 5 9

我们定义一个矩阵 $\textit{sum}$ 使得 $\textit{sum}_{x,y} = \sum\limits_{i=1}^x \sum\limits_{j=1}^y a_{i,j}$，

那么这个矩阵长这样：

1  3  7  10
6  9  15 22
12 18 29 45

第一个问题就是递推求 $\textit{sum}$ 的过程，$\textit{sum}_{i,j} = \textit{sum}_{i - 1,j} + \textit{sum}_{i,j - 1} - \textit{sum}_{i - 1,j - 1} + a_{i,j}$。

因为同时加了 $\textit{sum}_{i - 1,j}$ 和 $\textit{sum}_{i,j - 1}$，故重复了 $\textit{sum}_{i - 1,j - 1}$，减去。

第二个问题就是如何应用，譬如求 $(x_1,y_1) - (x_2,y_2)$ 子矩阵的和。

那么，根据类似的思考过程，易得答案为 $\textit{sum}_{x_2,y_2} - \textit{sum}_{x_1 - 1,y_2} - sum_{x_2,y_1 - 1} + sum_{x_1 - 1,y_1 - 1}$。

例题: 洛谷 P1387 最大正方形

在一个 $n\times m$ 的只包含 $0$ 和 $1$ 的矩阵里找出一个不包含 $0$ 的最大正方形，输出边长。

参考代码

#include <algorithm>
#include <iostream>
using namespace std;
int a[103][103];
int b[103][103];  // 前缀和数组，相当于上文的 sum[]
int main() {
    int n, m;
    cin >> n >> m;

    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            cin >> a[i][j];
            b[i][j] =
                b[i][j - 1] + b[i - 1][j] - b[i - 1][j - 1] + a[i][j];  // 求前缀和
        }
    }

    int ans = 1;

    int l = 2;
    while (l <= min(n, m)) {  //判断条件
        for (int i = l; i <= n; i++) {
            for (int j = l; j <= m; j++) {
                if (b[i][j] - b[i - l][j] - b[i][j - l] + b[i - l][j - l] == l * l) {
                    ans = max(ans, l);  //在这里统计答案
                }
            }
        }
        l++;
    }

    cout << ans << endl;
    return 0;
}

基于 DP 计算高维前缀和

基于容斥原理来计算高维前缀和的方法，其优点在于形式较为简单，无需特别记忆，但当维数升高时，其复杂度较高。这里介绍一种基于 DP 计算高维前缀和的方法。该方法即通常语境中所称的 高维前缀和。

设高维空间 $U$ 共有 $D$ 维，需要对 $f[\cdot]$ 求高维前缀和 $\text{sum}[\cdot]$。令 $\text{sum}[i][\text{state}]$ 表示同 $\text{state}$ 后 $D - i$ 维相同的所有点对于 $\text{state}$ 点高维前缀和的贡献。由定义可知 $\text{sum}[0][\text{state}] = f[\text{state}]$，以及 $\text{sum}[\text{state}] = \text{sum}[D][\text{state}]$。

其递推关系为 $\text{sum}[i][\text{state}] = \text{sum}[i - 1][\text{state}] + \text{sum}[i][\text{state}']$，其中 $\text{state}'$ 为第 $i$ 维恰好比 $\text{state}$ 少 $1$ 的点。该方法的复杂度为 $O(D \times |U|)$，其中 $|U|$ 为高维空间 $U$ 的大小。

一种实现的伪代码如下：

for state
  sum[state] = f[state];
for(i = 0;i <= D;i += 1)
  for 以字典序从小到大枚举 state
    sum[state] += sum[state'];

树上前缀和

设 $\textit{sum}_i$ 表示结点 $i$ 到根节点的权值总和。
然后：

• 若是点权，$x,y$ 路径上的和为 $\textit{sum}_x + \textit{sum}_y - \textit{sum}_\textit{lca} - \textit{sum}_{\textit{fa}_\textit{lca}}$。

• 若是边权，$x,y$ 路径上的和为 $\textit{sum}_x + \textit{sum}_y - 2\cdot\textit{sum}_{lca}$。

  LCA 的求法参见 最近公共祖先。

差分

普通差分

差分是一种和前缀和相对的策略，可以当做是求和的逆运算。

这种策略的定义是令 $b_i=\begin{cases}a_i-a_{i-1}\,&i \in[2,n] \\ a_1\,&i=1\end{cases}$

简单性质：

• $a_i$ 的值是 $b_i$ 的前缀和，即 $a_n=\sum\limits_{i=1}^nb_i$
• 计算 $a_i$ 的前缀和 $sum=\sum\limits_{i=1}^na_i=\sum\limits_{i=1}^n\sum\limits_{j=1}^{i}b_j=\sum\limits_{i}^n(n-i+1)b_i=(n+1)\sum\limits_{i}^{n}b_i-\sum\limits_{i}^nib_i$

它可以维护多次对序列的一个区间加上一个数，并在最后询问某一位的数或是多次询问某一位的数。注意修改操作一定要在查询操作之前。

示例

譬如使 $[l,r]$ 中的每个数加上一个 $k$，即

$$\begin{align*} b_l &\leftarrow b_l + k\\ b_{r + 1} &\leftarrow b_{r + 1} - k \end{align*}$$

其中

$$\begin{align*} b_l+k&=a_l+k-a_{l-1}\\ b_{r+1}-k&=a_{r+1}-(a_r+k) \end{align*}$$

最后做一遍前缀和就好了。

C++ 标准库中实现了差分函数 std::adjacent_difference，定义于头文件 <numeric> 中。

一维差分代码

//给区间[l, r]中的每个数加上c：
void insert(int l, int r, int c){
    B[l] += c; 
    B[r + 1] -= c;
}
//输入a[i]，构建差分数组B
for (int i = 1; i <= n; ++i) {
    cin >> a[i];
    add(i, i, a[i]);
    //或者b[i] = a[i] - a[i - 1];
}

二维差分代码

//给以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵中的所有元素加上c：
void insert(int x1, int y1, int x2, int y2, int c){
    b[x1][y1] += c;
    b[x1][y2 + 1] -= c;
    b[x2 + 1][y1] -= c;
    b[x2 + 1][y2 + 1] += c;
}

树上差分

树上差分可以理解为对树上的某一段路径进行差分操作，这里的路径可以类比一维数组的区间进行理解。例如在对树上的一些路径进行频繁操作，并且询问某条边或者某个点在经过操作后的值的时候，就可以运用树上差分思想了。

树上差分通常会结合 树基础 和 最近公共祖先 来进行考察。树上差分又分为 点差分 与 边差分，在实现上会稍有不同。

点差分

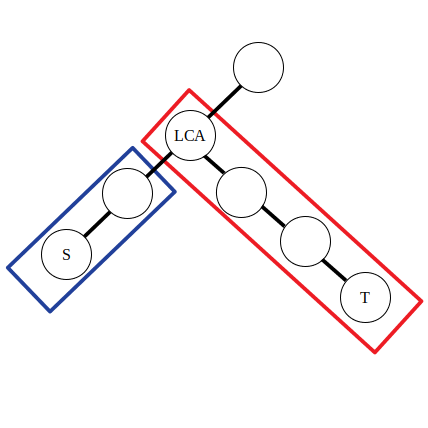
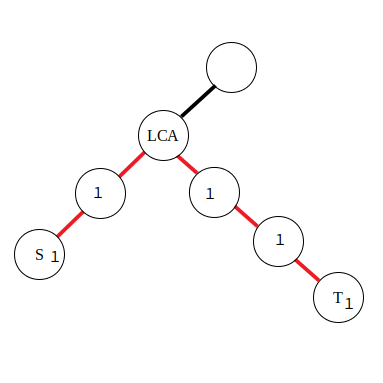
举例：对域树上的一些路径 $\delta(s_1,t_1), \delta(s_2,t_2), \delta(s_3,t_3)\dots$ 进行访问，问一条路径 $\delta(s,t)$ 上的点被访问的次数。

对于一次 $\delta(s,t)$ 的访问，需要找到 $s$ 与 $t$ 的公共祖先，然后对这条路径上的点进行访问（点的权值加一），若采用 DFS 算法对每个点进行访问，由于有太多的路径需要访问，时间上承受不了。这里进行差分操作：

$$\begin{aligned} &d_s\leftarrow d_s+1\\ &d_{lca}\leftarrow d_{\textit{lca}}-1\\ &d_t\leftarrow d_t+1\\ &d_{f(\textit{lca})}\leftarrow d_{f(\textit{lca})}-1\\ \end{aligned}$$

其中 $f(x)$ 表示 $x$ 的父亲节点，$d_i$ 为点权 $a_i$ 的差分数组。

可以认为公式中的前两条是对蓝色方框内的路径进行操作，后两条是对红色方框内的路径进行操作。不妨令 $\textit{lca}$ 左侧的直系子节点为 $\textit{left}$。那么有 $d_{\textit{lca}}-1=a_{\textit{lca}}-(a_{\textit{left}}+1)$，$d_{f(\textit{lca})}-1=a_{f(\textit{lca})}-(a_{\textit{lca}}+1)$。可以发现实际上点差分的操作和上文一维数组的差分操作是类似的。

边差分

若是对路径中的边进行访问，就需要采用边差分策略了，使用以下公式：

$$\begin{aligned} &d_s\leftarrow d_s+1\\ &d_t\leftarrow d_t+1\\ &d_{\textit{lca}}\leftarrow d_{\textit{lca}}-2\\ \end{aligned}$$

由于在边上直接进行差分比较困难，所以将本来应当累加到红色边上的值向下移动到附近的点里，那么操作起来也就方便了。对于公式，有了点差分的理解基础后也不难推导，同样是对两段区间进行差分。

例题: 洛谷 3128 最大流

FJ 给他的牛棚的 $N(2 \le N \le 50,000)$ 个隔间之间安装了 $N-1$ 根管道，隔间编号从 $1$ 到 $N$。所有隔间都被管道连通了。
FJ 有 $K(1 \le K \le 100,000)$ 条运输牛奶的路线，第 $i$ 条路线从隔间 $s_i$ 运输到隔间 $t_i$。一条运输路线会给它的两个端点处的隔间以及中间途径的所有隔间带来一个单位的运输压力，你需要计算压力最大的隔间的压力是多少。

解题思路
需要统计每个点经过了多少次，那么就用树上差分将每一次的路径上的点加一，可以很快得到每个点经过的次数。这里采用倍增法计算 LCA，最后对 DFS 遍历整棵树，在回溯时对差分数组求和就能求得答案了。

参考代码

#include <bits/stdc++.h>

using namespace std;
#define maxn 50010

struct node {
  int to, next;
} edge[maxn << 1];

int fa[maxn][30], head[maxn << 1];
int power[maxn];
int depth[maxn], lg[maxn];
int n, k, ans = 0, tot = 0;

void add(int x, int y) {  //加边
  edge[++tot].to = y;
  edge[tot].next = head[x];
  head[x] = tot;
}

void dfs(int now, int father) {  // dfs求最大压力
  fa[now][0] = father;
  depth[now] = depth[father] + 1;
  for (int i = 1; i <= lg[depth[now]]; ++i)
    fa[now][i] = fa[fa[now][i - 1]][i - 1];
  for (int i = head[now]; i; i = edge[i].next)
    if (edge[i].to != father) dfs(edge[i].to, now);
}

int lca(int x, int y) {  //求LCA，最近公共祖先
  if (depth[x] < depth[y]) swap(x, y);
  while (depth[x] > depth[y]) x = fa[x][lg[depth[x] - depth[y]] - 1];
  if (x == y) return x;
  for (int k = lg[depth[x]] - 1; k >= 0; k--) {
    if (fa[x][k] != fa[y][k]) x = fa[x][k], y = fa[y][k];
  }
  return fa[x][0];
}

//用dfs求最大压力，回溯时将子树的权值加上
void get_ans(int u, int father) {
  for (int i = head[u]; i; i = edge[i].next) {
    int to = edge[i].to;
    if (to == father) continue;
    get_ans(to, u);
    power[u] += power[to];
  }
  ans = max(ans, power[u]);
}

int main() {
  scanf("%d %d", &n, &k);
  int x, y;
  for (int i = 1; i <= n; i++) {
    lg[i] = lg[i - 1] + (1 << lg[i - 1] == i);
  }
  for (int i = 1; i <= n - 1; i++) {  //建图
    scanf("%d %d", &x, &y);
    add(x, y);
    add(y, x);
  }
  dfs(1, 0);
  int s, t;
  for (int i = 1; i <= k; i++) {
    scanf("%d %d", &s, &t);
    int ancestor = lca(s, t);
    // 树上差分
    power[s]++;
    power[t]++;
    power[ancestor]--;
    power[fa[ancestor][0]]--;
  }
  get_ans(1, 0);
  printf("%d\n", ans);
  return 0;
}

习题

---

前缀和

• 洛谷 U53525 前缀和（例题）
• 洛谷 U69096 前缀和的逆
• AT2412 最大の和
• 「USACO16JAN」子共七 Subsequences Summing to Sevens

---

二维/多维前缀和

• HDU 6514 Monitor
• 洛谷 P1387 最大正方形
• 「HNOI2003」激光炸弹

---

树上前缀和

• LOJ 10134.Dis
• LOJ 2491. 求和

---

差分

• 树状数组 3：区间修改，区间查询
• P3397 地毯
• 「Poetize6」IncDec Sequence

---

树上差分

• 洛谷 3128 最大流
• JLOI2014 松鼠的新家
• NOIP2015 运输计划
• NOIP2016 天天爱跑步