主要参考算法导论,修正原文错误、易混淆翻译,整合相关习题实战
字符串匹配
在编辑文本程序过程中, 我们经常需要在文本中找到某个模式的所有出现位置。典型情况 是, 一段正在被编辑的文本构成一个文件, 而所要搜寻的模式是用户正在输入的特定的关键字。 有效地解决这个问题的算法叫做字符串匹配算法, 该算法能够极大提高编辑文本程序时的响应 效率。在其他很多应用中, 字符串匹配算法用于在 DNA 序列中搜寻特定的序列。在网络搜索引 擎中也需要用这种方法来找到所要查询的网页地址。
字符串匹配问题的形式化定义如下: 假设文本是一个长度为 n n n T [ 1 , n ] T[1, n] T [ 1 , n ] m m m P [ 1.. m ] P[1 . . m] P [ 1.. m ] m ⩽ n m \leqslant n m ⩽ n P P P T T T Σ \Sigma Σ Σ = { 0 , 1 } \Sigma=\{0,1\} Σ = { 0 , 1 } Σ = { a , b , ⋯ , z } \Sigma=\{a, b, \cdots, z\} Σ = { a , b , ⋯ , z } P P P T T T
如图 32-1 所示, 如果 0 ⩽ s ⩽ n − m 0 \leqslant s \leqslant n-m 0 ⩽ s ⩽ n − m T [ s + 1 … s + m ] = P [ 1 … m ] T[s+1 \ldots s+m]=P[1 \ldots m] T [ s + 1 … s + m ] = P [ 1 … m ] T [ s + j ] = T[s+j]= T [ s + j ] = P [ j ] P[j] P [ j ] 1 ⩽ j ⩽ m 1 \leqslant j \leqslant m 1 ⩽ j ⩽ m P P P T T T s s s P P P T T T s + 1 s+1 s + 1 P P P T T T s s s s s s P P P T T T
图 32-1
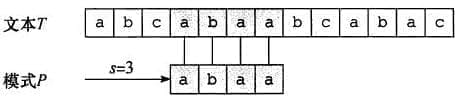
字符串匹配问题的一个例子, 在该例子中, 我们试图找到模式 P = a b a a P=\mathrm{abaa} P = abaa T = a b c a b a a b c a b a c T=a b c a b a a b c a b a c T = ab c abaab c aba c s = 3 s=3 s = 3 s s s
除了在 32.1 32.1 32.1 Θ ( ( n − m + 1 ) m ) \Theta((n-m+1) m) Θ (( n − m + 1 ) m ) P P P O ( m ∣ Σ ∣ ) O(m|\Sigma|) O ( m ∣Σ∣ ) Θ ( n ) \Theta(n) Θ ( n ) 32.4 32.4 32.4 Θ ( n ) \Theta(n) Θ ( n ) Θ ( m ) \Theta(m) Θ ( m )
符号和术语
在本章中, 我们只考虑有限长度的字符串。我们用 Σ ∗ \Sigma^{\ast} Σ ∗ Σ \Sigma Σ ε \varepsilon ε Σ ∗ \Sigma^{\ast} Σ ∗ x x x ∣ x ∣ |x| ∣ x ∣ x x x y y y 连结 (concatenation)用 x y x y x y ∣ x ∣ + ∣ y ∣ |x|+|y| ∣ x ∣ + ∣ y ∣ x x x y y y
如果对某个字符串 y ∈ Σ ∗ y \in \Sigma^{\ast} y ∈ Σ ∗ x = w y x=w y x = w y w w w x x x 前缀 , 记作 w ⊏ x w \sqsubset x w ⊏ x w ⊏ x w \sqsubset x w ⊏ x ∣ w ∣ ⩽ ∣ x ∣ |w| \leqslant|x| ∣ w ∣ ⩽ ∣ x ∣ y y y x = y w x=y w x = y w w w w x x x w ⊐ x w \sqsupset x w ⊐ x w ⊐ x w \sqsupset x w ⊐ x ∣ w ∣ ⩽ ∣ x ∣ |w| \leqslant|x| ∣ w ∣ ⩽ ∣ x ∣ a b ⊏ a b c c a \mathrm{ab} \sqsubset \mathrm{abcca} ab ⊏ abcca c c a ⊐ a b c c a cca \sqsupset a b c c a cc a ⊐ ab cc a ε \varepsilon ε x x x y y y a a a x a ⊐ y a x a \sqsupset y a x a ⊐ y a x ⊐ y x \sqsupset y x ⊐ y ⊏ \sqsubset ⊏ ⊐ \sqsupset ⊐
引理 32. 1(后缀重叠引理) 假设 x , y x, y x , y z z z x ⊐ z x \sqsupset z x ⊐ z y ⊐ z y \sqsupset z y ⊐ z ∣ x ∣ ⩽ ∣ y ∣ |x| \leqslant|y| ∣ x ∣ ⩽ ∣ y ∣ x ⊐ y x \sqsupset y x ⊐ y ∣ x ∣ ⩾ ∣ y ∣ |x| \geqslant|y| ∣ x ∣ ⩾ ∣ y ∣ y ⊐ x y \sqsupset x y ⊐ x ∣ x ∣ = ∣ y ∣ |x|=|y| ∣ x ∣ = ∣ y ∣ x = y x=y x = y
为了使符号简洁, 我们把模式 P [ 1.. m ] P[1 . . m] P [ 1.. m ] k k k P [ 1 … k ] P[1 \ldots k] P [ 1 … k ] P k P_{k} P k P 0 = ε , P m = P = P [ 1.. m ] P_{0}=\varepsilon, P_{m}=P=P[1 . . m] P 0 = ε , P m = P = P [ 1.. m ] T T T k k k T k T_{k} T k s ( 0 ⩽ s ⩽ n − m ) s(0 \leqslant s \leqslant n-m) s ( 0 ⩽ s ⩽ n − m ) P ⊐ T s + m P \sqsupset T_{s+m} P ⊐ T s + m
在我们的伪代码中, 把比较两个等长字符串是否相等的操作当做操作原语。如果字符串比较是从左到右进行的, 并且当遇到一个字符不匹配时, 比较操作终止, 则可以假设在这样的一个检测中所花费的时间是关于已匹配成功字符数目的线性函数。更准确地说, 假设检测“ x = = y x==y x == y Θ ( t + 1 ) \Theta(t+1) Θ ( t + 1 ) t t t z ⊏ x z \sqsubset x z ⊏ x z ⊏ y z \sqsubset y z ⊏ y z z z Θ ( t + 1 ) \Theta(t+1) Θ ( t + 1 ) Θ ( t ) \Theta(t) Θ ( t ) t = 0 t=0 t = 0
朴素字符串匹配算法
朴素字符串匹配算法是通过一个循坏找到所有有效偏移, 该循环对 n − m + 1 n-m+1 n − m + 1 s s s P [ 1.. m ] = T [ s + 1.. s + m ] P[1 . . m]=T[s+1 . . s+m] P [ 1.. m ] = T [ s + 1.. s + m ]
NAIVE-STRING-MATCHER ( T , P ) 1 n = T . length 2 m = P . length 3 for s = 0 to n − m 4 if P [ 1.. m ] = = T [ s + 1.. s + m ] 5 print "Pattern occurs with shift" s \begin{aligned}
&\text { NAIVE-STRING-MATCHER }(T, P) \\
&1 \quad n=T . \text { length } \\
&2 \quad m=P . \text { length } \\
&3 \quad \text { for } s=0 \text { to } n-m \\
&4 \quad \quad \text { if } P[1 . . m]==T[s+1 . . s+m] \\
&5\quad \quad \quad\text { print "Pattern occurs with shift" } s
\end{aligned}
NAIVE-STRING-MATCHER ( T , P ) 1 n = T . length 2 m = P . length 3 for s = 0 to n − m 4 if P [ 1.. m ] == T [ s + 1.. s + m ] 5 print "Pattern occurs with shift" s
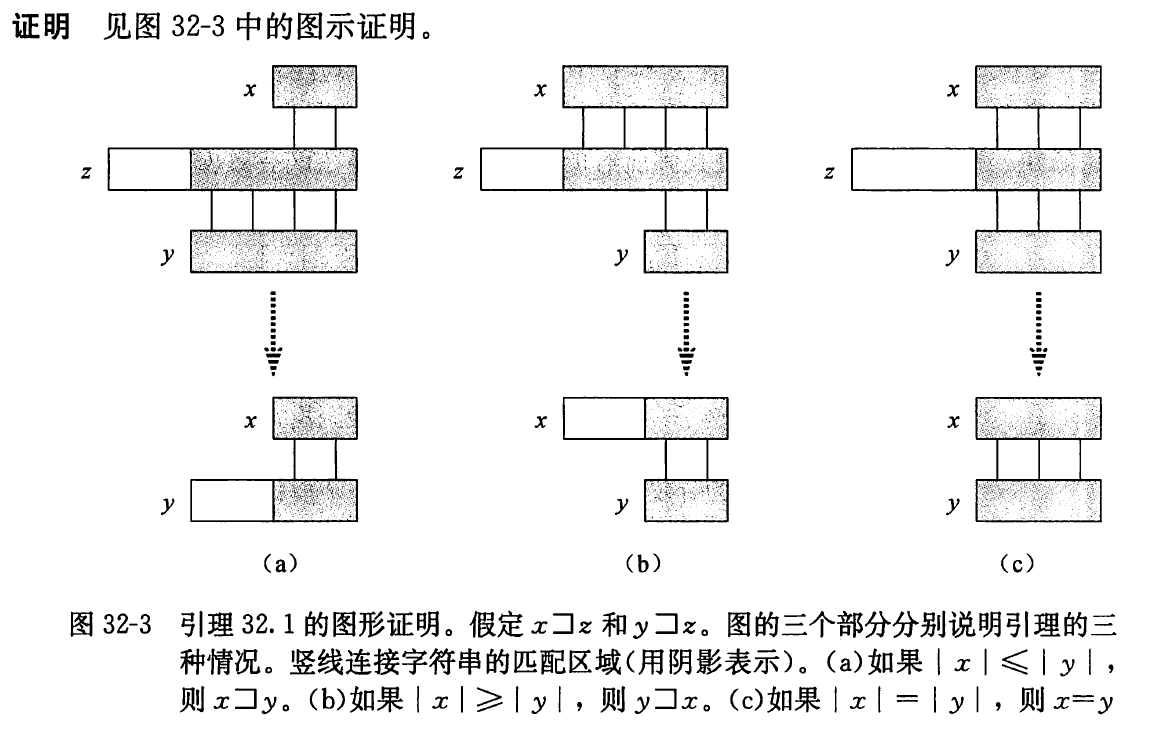
图 32-4 描绘的朴素字符串匹配过程可以形象地看成一个包含模式的“模板”沿文本滑动, 同时对每个偏移都要检测模板上的字符是否与文本中对应的字符相等。第 3 ∼ 5 3 \sim 5 3 ∼ 5 s s s
在最坏情况下, 朴素字符串匹配算法运行时间为 O ( ( n − m + 1 ) m ) O((n-m+1) m) O (( n − m + 1 ) m ) a n a^{n} a n n n n a a a a m a^{m} a m s s s n − m + 1 n-m+1 n − m + 1 m m m Θ ( ( n − m + 1 ) m ) \Theta((n-m+1) m) Θ (( n − m + 1 ) m ) m = ⌊ n / 2 ⌋ m=\lfloor n / 2\rfloor m = ⌊ n /2 ⌋ Θ ( n 2 ) \Theta\left(n^{2}\right) Θ ( n 2 )
我们将会看到, NAIVE-STRINGMATCHER 并不是解决字符串匹配问题的最好过程。事实上, 在本章中, 我们将会发现 Knuth-Morris-Pratt 算法在最坏情况下比朴素算法好得多。这种朴素字符串匹配算法效率不高, 是因为当其他无效的 s s s s s s s s s P = a a b P=a a b P = aab s = 0 s=0 s = 0 T [ 4 ] = b T[4]=b T [ 4 ] = b
Rabin-Karp 算法(字符串前缀哈希)
在实际应用中, Rabin 和 Karp 所提出的字符串匹配算法能够较好地运行, 并且还可以从中归纳出相关问题的其他算法, 比如二维模式匹配。 Rabin-Karp算法的预处理时间是 Θ ( m ) \Theta(m) Θ ( m ) Θ ( ( n − m + 1 ) m ) \Theta((n-m+1) m) Θ (( n − m + 1 ) m )
该算法运用了初等数论概念, 比如两个数相对于第三个数模等价。如果想要了解相关的定义, 请参照 31.1 31.1 31.1
为了便于说明, 假设 Σ = { 0 , 1 , 2 , ⋯ , 9 } \Sigma=\{0,1,2, \cdots, 9\} Σ = { 0 , 1 , 2 , ⋯ , 9 } d d d d = ∣ Σ ∣ d=|\Sigma| d = ∣Σ∣ k k k k k k
给定一个模式 P [ 1.. m ] P[1 . . m] P [ 1.. m ] p p p T [ 1.. n ] T[1 . . n] T [ 1.. n ] t s t_{s} t s m m m T [ s + 1 … s + m ] T[s+1 \ldots s+m] T [ s + 1 … s + m ] s = 0 , 1 , ⋯ , n − m s=0,1, \cdots, n-m s = 0 , 1 , ⋯ , n − m T [ s + 1.. s + m ] = P [ 1.. m ] T[s+1 . . s+m]=P[1 . . m] T [ s + 1.. s + m ] = P [ 1.. m ] t s = p t_{s}=p t s = p Θ ( m ) \Theta(m) Θ ( m ) p p p Θ ( n − m + 1 ) \Theta(n-m+1) Θ ( n − m + 1 ) t s t_{s} t s p p p t s t_{s} t s Θ ( m ) + Θ ( n − \Theta(m)+\Theta(n- Θ ( m ) + Θ ( n − m + 1 ) = Θ ( n ) m+1)=\Theta(n) m + 1 ) = Θ ( n ) s s s p p p t s t_{s} t s
我们可以运用霍纳法则(参见 30.1 30.1 30.1 Θ ( m ) \Theta(m) Θ ( m ) p p p
p = P [ m ] + 10 ( P [ m − 1 ] + 10 ( P [ m − 2 ] + ⋯ + 10 ( P [ 2 ] + 10 P [ 1 ] ) ⋯ ) ) p=P[m]+10(P[m-1]+10(P[m-2]+\cdots+10(P[2]+10 P[1]) \cdots))
p = P [ m ] + 10 ( P [ m − 1 ] + 10 ( P [ m − 2 ] + ⋯ + 10 ( P [ 2 ] + 10 P [ 1 ]) ⋯ ))
类似地, 也可以在 Θ ( m ) \Theta(m) Θ ( m ) T [ 1.. m ] T[1 . . m] T [ 1.. m ] t 0 t_{0} t 0
为了在时间 Θ ( n − m ) \Theta(n-m) Θ ( n − m ) t 1 , t 2 , ⋯ , t n − m t_{1}, t_{2}, \cdots, t_{n-m} t 1 , t 2 , ⋯ , t n − m t s t_{s} t s t s + 1 t_{s+1} t s + 1
t s + 1 = 10 ( t s − 1 0 m − 1 T [ s + 1 ] ) + T [ s + m + 1 ] t_{s+1}=10\left(t_{s}-10^{m-1} T[s+1]\right)+T[s+m+1]
t s + 1 = 10 ( t s − 1 0 m − 1 T [ s + 1 ] ) + T [ s + m + 1 ]
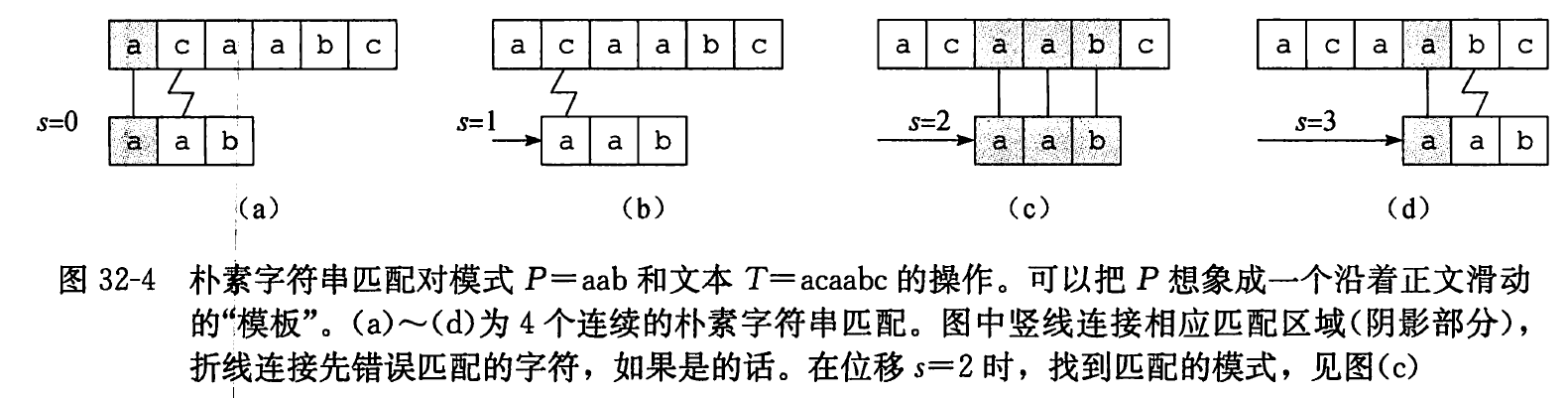
减去 1 0 m − 1 T [ s + 1 ] 10^{m-1} T[s+1] 1 0 m − 1 T [ s + 1 ] t s t_{s} t s T [ s + m + 1 ] T[s+m+1] T [ s + m + 1 ] m = 5 m=5 m = 5 t s = 31415 t_{s}=31415 t s = 31415 T [ s + 1 ] = 3 T[s+1]=3 T [ s + 1 ] = 3 ( ( ( T [ s + 5 + 1 ] = 2 ) T[s+5+1]=2) T [ s + 5 + 1 ] = 2 )
t s + 1 = 10 ( 31415 − 1000.3 ) + 2 = 14152 ( 32.1 ) t_{s+1}=10(31415-1000.3)+2=14152 \quad \quad(32.1)
t s + 1 = 10 ( 31415 − 1000.3 ) + 2 = 14152 ( 32.1 )
如果能够预先计算出常数 1 0 m − 1 10^{m-1} 1 0 m − 1 31.6 31.6 31.6 O ( lg m ) O(\lg m) O ( lg m ) O ( m ) O(m) O ( m ) ( 32.1 ) (32.1) ( 32.1 ) Θ ( m ) \Theta(m) Θ ( m ) p p p Θ ( n − m + 1 ) \Theta(n-m+1) Θ ( n − m + 1 ) t 0 , t 1 , t 2 , ⋯ , t n − m t_{0}, t_{1}, t_{2}, \cdots, t_{n-m} t 0 , t 1 , t 2 , ⋯ , t n − m Θ ( m ) \Theta(m) Θ ( m ) Θ \Theta Θ ( n − m + 1 ) (n-m+1) ( n − m + 1 ) P [ 1.. m ] P[1 . . m] P [ 1.. m ] T [ 1.. n ] T[1 . . n] T [ 1.. n ]
到目前为止, 我们有意回避的一个问题是: p p p t s t_{s} t s P P P m m m p p p m m m ) ) ) q q q p p p t s t_{s} t s Θ ( m ) \Theta(m) Θ ( m ) q q q p p p Θ ( n − m + 1 ) \Theta(n-m+1) Θ ( n − m + 1 ) q q q t s t_{s} t s q q q 10 q 10 q 10 q d d d { 0 , 1 , ⋯ , d − 1 } \{0,1, \cdots, d-1\} { 0 , 1 , ⋯ , d − 1 } q q q d q d q d q q q q
t s + 1 = ( d ( t s − T [ s + 1 ] h ) + T [ s + m + 1 ] ) m o d q ( 32.2 ) t_{s+1}=\left(d\left(t_{s}-T[s+1] h\right)+T[s+m+1]\right) \bmod q \quad \quad(32.2)
t s + 1 = ( d ( t s − T [ s + 1 ] h ) + T [ s + m + 1 ] ) mod q ( 32.2 )
其中 h ≡ d m − 1 ( m o d q ) h \equiv d^{m-1}(\bmod q) h ≡ d m − 1 ( mod q ) m m m
但是基于模 q q q t s ≡ p ( m o d q ) t_{s} \equiv p(\bmod q) t s ≡ p ( mod q ) t s = p t_{s}=p t s = p t s ≠ p ( m o d q ) t_{s} \neq p(\bmod q) t s = p ( mod q ) t s ≠ p t_{s} \neq p t s = p s s s t s ≡ p ( m o d q ) t_{s} \equiv p(\bmod q) t s ≡ p ( mod q ) s s s t s ≡ p ( m o d q ) t_{s} \equiv p(\bmod q) t s ≡ p ( mod q ) s s s s s s P [ 1.. m ] = T [ s + 1 … s + m ] P[1 . . m]=T[s+1 \ldots s+m] P [ 1.. m ] = T [ s + 1 … s + m ] q q q
下面的过程准确描述了上述思想。过程的输入是文本 T T T P P P d d d ∣ Σ ∣ |\Sigma| ∣Σ∣ q q q
RABIN-KARP-MATCHER ( T , P , d , q ) 1 n = T . length 2 m = P . length 3 h = d m − 1 m o d q 4 p = 0 5 t 0 = 0 6 for i = 1 to m 7 p = ( d p + P [ i ] ) m o d q 8 t 0 = ( d t 0 + T [ i ] ) m o d q 9 for s = 0 to n − m 10 if p = = t s 11 if P [ 1.. m ] = = T [ s + 1.. s + m ] 12 print “Pattern occurs with shift” s 13 if s < n − m 14 t s + 1 = ( d ( t s − T [ s + 1 ] h ) + T [ s + m + 1 ] ) m o d q \begin{aligned}
&\text {RABIN-KARP-MATCHER }(T, P, d, q) \\
1 & \quad n=T . \text { length } \\
2 & \quad m=P . \text { length } \\
3 & \quad h=d^{m-1} \bmod q \\
4 & \quad p=0 \\
5 & \quad t_{0}=0 \\
6 & \quad \text {for } i=1 \text { to } \mathrm{m} \\
7 & \quad \quad p=(d p+P[i]) \bmod q \\
8 & \quad \quad t_{0}=\left(d t_{0}+T[i]\right) \bmod q \\
9 & \quad \text {for } s=0 \text { to } n-m \\
10 & \quad \quad \text {if } p==t_{s} \\
11 & \quad \quad \quad \text {if } P[1 . . m]==T[s+1 . . s+m] \\
12 & \quad \quad \quad \quad \text {print } \text { “Pattern occurs with shift” } s \\
13 & \quad \quad \text {if } s<n-m \\
14 & \quad \quad \quad t_{s+1}=\left(d\left(t_{s}-T[s+1] h\right)+T[s+m+1]\right) \bmod q
\end{aligned}
1 2 3 4 5 6 7 8 9 10 11 12 13 14 RABIN-KARP-MATCHER ( T , P , d , q ) n = T . length m = P . length h = d m − 1 mod q p = 0 t 0 = 0 for i = 1 to m p = ( d p + P [ i ]) mod q t 0 = ( d t 0 + T [ i ] ) mod q for s = 0 to n − m if p == t s if P [ 1.. m ] == T [ s + 1.. s + m ] print “Pattern occurs with shift” s if s < n − m t s + 1 = ( d ( t s − T [ s + 1 ] h ) + T [ s + m + 1 ] ) mod q
RABIN-KARP-MATCHER 执行过程如下。所有的字符都假设是 d d d t t t m m m h h h 4 ∼ 8 4 \sim 8 4 ∼ 8 P [ 1.. m ] m o d q P[1 . . m] \bmod q P [ 1.. m ] mod q p p p T [ 1.. m ] m o d q T[1 . . m] \bmod q T [ 1.. m ] mod q t 0 t_{0} t 0 9 ∼ 14 9 \sim 14 9 ∼ 14 s s s
第 10 行无论何时执行, 都有 t s = T [ s + 1 … s + m ] m o d q t_{s}=T[s+1 \ldots s+m] \bmod q t s = T [ s + 1 … s + m ] mod q
如果在第 10 行中有 p = t s p=t_{s} p = t s P [ 1.. m ] = T [ s + 1 … s + m ] P[1 . . m]=T[s+1 \ldots s+m] P [ 1.. m ] = T [ s + 1 … s + m ] s < n − m s<n-m s < n − m t s m o d q t_{s} \bmod q t s mod q t s + 1 m o d q t_{s+1} \bmod q t s + 1 mod q
RABIN-KARP-MATCHER 的预处理时间为 Θ ( m ) \Theta(m) Θ ( m ) Θ ( ( n − m + 1 ) m ) \Theta((n-m+1) m) Θ (( n − m + 1 ) m ) P = a m P=a^{m} P = a m T = a n T=a^{n} T = a n n − m + 1 n-m+1 n − m + 1 Θ ( ( n − m + 1 ) m ) \Theta((n-m+1) m) Θ (( n − m + 1 ) m )
在许多实际应用中, 我们希望有效偏移的个数少一些 (如只有常数 c c c O ( ( n − m + 1 ) + c m ) = O ( n + m ) O((n-m+1)+c m)=O(n+m) O (( n − m + 1 ) + c m ) = O ( n + m ) q q q Σ ∗ \Sigma^{\ast} Σ ∗ Z q \mathbf{Z}_{q} Z q 11.3.1 11.3 .1 11.3.1 q q q O ( n / q ) O(n / q) O ( n / q ) t s t_{s} t s q q q p p p 1 / q 1 / q 1/ q O ( n ) O(n) O ( n ) O ( m ) O(m) O ( m )
O ( n ) + O ( m ( v + n / q ) ) O(n)+O(m(v+n / q))
O ( n ) + O ( m ( v + n / q ))
其中 v v v v = O ( 1 ) v=O(1) v = O ( 1 ) q ⩾ m q \geqslant m q ⩾ m O ( n ) O(n) O ( n ) ( O ( 1 ) ) (O(1)) ( O ( 1 )) q q q O ( n + m ) O(n+m) O ( n + m ) m ⩽ n m \leqslant n m ⩽ n O ( n ) O(n) O ( n )
利用有限自动机进行字符串匹配
很多字符串匹配算法都要建立一个有限自动机, 它是一个处理信息的简单机器, 通过对文本字符串 T T T P P P Θ ( n ) \Theta(n) Θ ( n ) Σ \Sigma Σ 32.4 32.4 32.4
本节首先定义有限自动机。然后, 我们要考察一种特殊的字符串匹配自动机, 并展示如何利用它找出一个模式在文本中的出现位置。最后, 我们将说明对一个给定的输入模式, 如何构造相应的字符串匹配自动机。
有限自动机
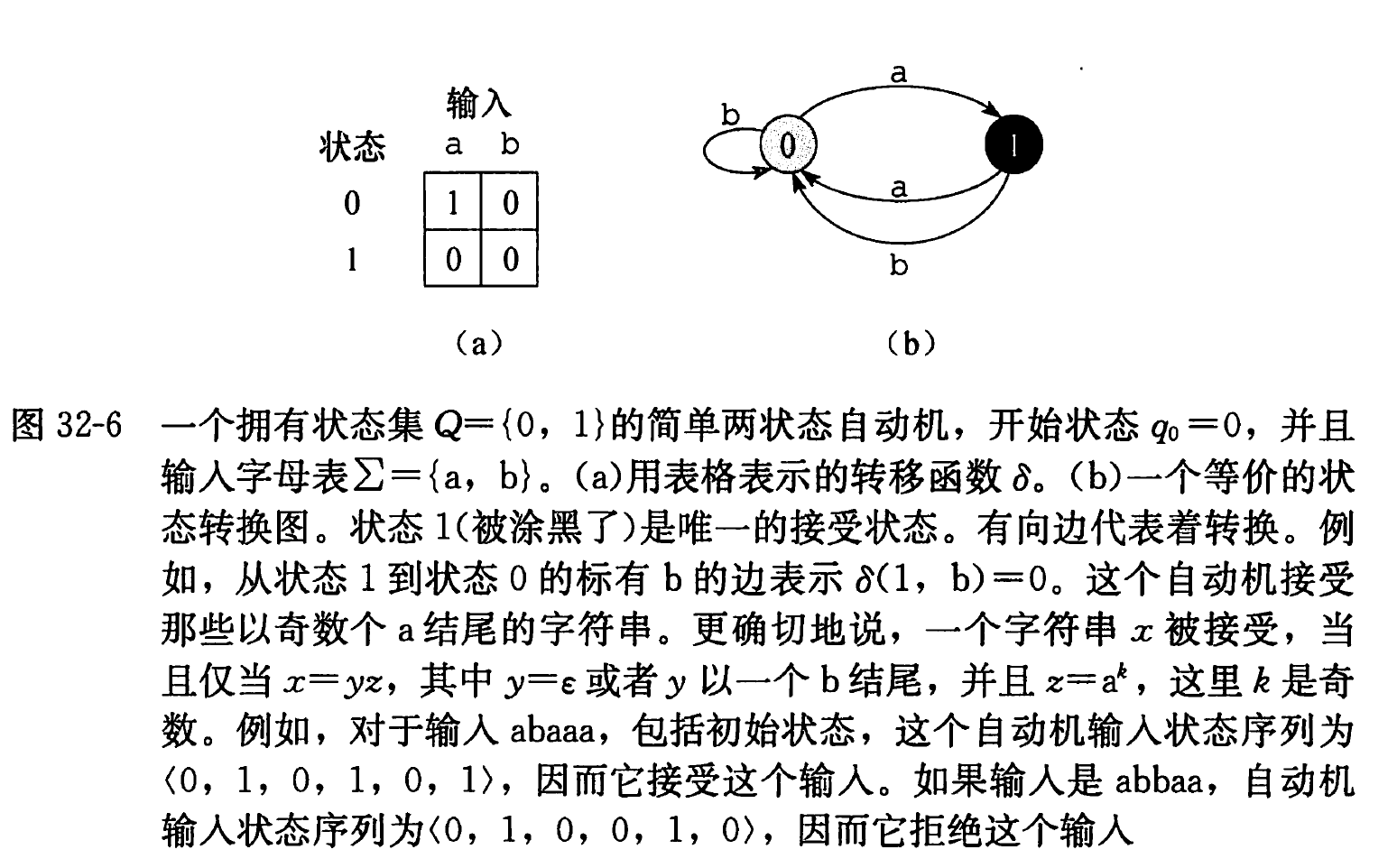
如图 32-6 所示, 一个有限自动机 M M M 是一个 5 元组 ( Q , q 0 , A , Σ , δ ) \left(Q, q_{0}, A, \Sigma, \delta\right) ( Q , q 0 , A , Σ , δ )
Q Q Q 状态 的有限集合。q o ∈ Q q_{o} \in Q q o ∈ Q 初始状态 。A ⊆ Q A \subseteq Q A ⊆ Q 接受状态 集合。∑ \sum ∑ δ \delta δ Q × ∑ Q \times \sum Q × ∑ Q Q Q M M M 转移函数 。
有限自动机开始于状态 q 0 q_{0} q 0 q q q a a a q q q δ ( q , a ) \delta(q, a) δ ( q , a ) q q q A A A M M M 接受 了迄今为止所读入的字符串。没有被接受的输入称为被拒绝 的输入。
有限自动机 M M M ϕ \phi ϕ 终态函数 , 它是从 Σ ∗ \Sigma^{\ast} Σ ∗ Q Q Q ϕ ( w ) \phi(w) ϕ ( w ) M M M w w w ϕ ( w ) ∈ A \phi(w) \in A ϕ ( w ) ∈ A M M M w w w ϕ \phi ϕ
ϕ ( ε ) = q 0 , ϕ ( w a ) = δ ( ϕ ( w ) , a ) , w ∈ Σ ∗ , a ∈ Σ \begin{aligned}
&\phi(\varepsilon)=q_{0}, \\
&\phi(w a)=\delta(\phi(w), a), \quad w \in \Sigma^{*}, a \in \Sigma
\end{aligned}
ϕ ( ε ) = q 0 , ϕ ( w a ) = δ ( ϕ ( w ) , a ) , w ∈ Σ ∗ , a ∈ Σ
字符串匹配自动机
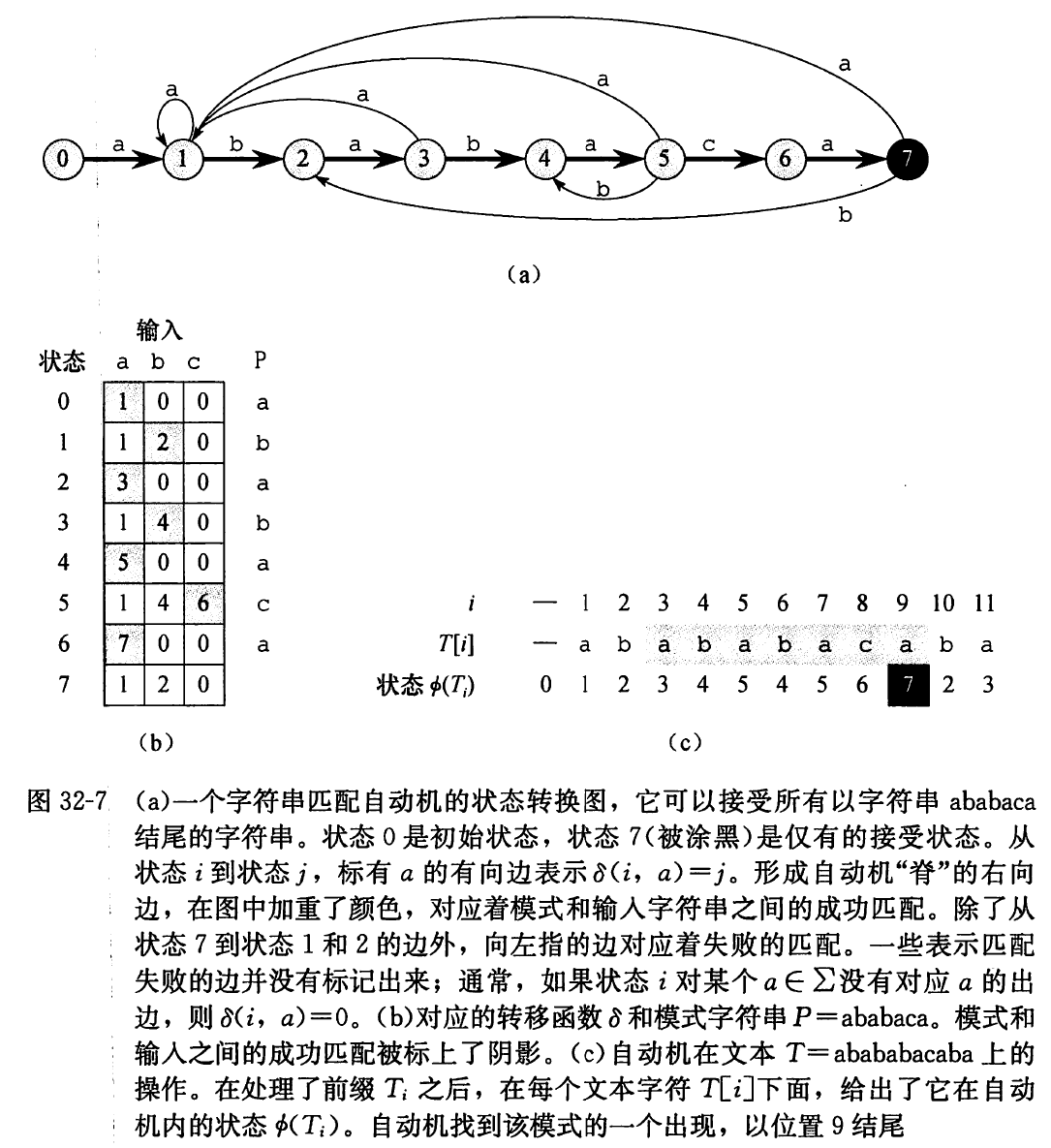
对于一个给定的模式 P P P P = a b a b a c a P=\mathrm{ababaca} P = ababaca P P P P P P
为了详细说明与给定模式 P [ 1.. m ] P[1 . . \mathrm{m}] P [ 1.. m ] σ \sigma σ P P P 后缀函数 。函数 σ \sigma σ Σ ∗ \Sigma^{\ast} Σ ∗ { 0 , 1 , ⋯ , m } \{0,1, \cdots, m\} { 0 , 1 , ⋯ , m } σ ( x ) \sigma(x) σ ( x ) P P P x x x
σ ( x ) = max { k : P k ⊐ x } ( 32.3 ) \sigma(x)=\max \left\{k: P_{k} \sqsupset x\right\} \quad \quad (32.3)
σ ( x ) = max { k : P k ⊐ x } ( 32.3 )
因为空字符串 P 0 = ε P_{0}=\varepsilon P 0 = ε σ \sigma σ P = P= P = a b \mathrm{ab} ab σ ( ε ) = 0 , σ ( c c a c a ) = 1 , σ ( c c a b ) = 2 \sigma(\varepsilon)=0, \sigma(ccaca )=1, \sigma( ccab )=2 σ ( ε ) = 0 , σ ( cc a c a ) = 1 , σ ( cc ab ) = 2 m m m P , σ ( x ) = m P, \sigma(x)=m P , σ ( x ) = m P ⊐ x P \sqsupset x P ⊐ x x ⊐ y x \sqsupset y x ⊐ y σ ( x ) ⩽ σ ( y ) \sigma (x) \leqslant \sigma(y) σ ( x ) ⩽ σ ( y )
给定模式 P [ 1.. m ] P[1..m] P [ 1.. m ]
状态集合 Q Q Q { 0 , 1 , ⋯ , m } \{0,1, \cdots, m\} { 0 , 1 , ⋯ , m } q 0 q_{0} q 0 m m m
对任意的状态 q q q a a a δ \delta δ
δ ( q , a ) = σ ( P q a ) \delta(q, a)=\sigma\left(P_{q} a\right)
δ ( q , a ) = σ ( P q a )
我们定义 δ ( q , a ) = σ ( P q a ) \delta(q, a)=\sigma\left(P_{q} a\right) δ ( q , a ) = σ ( P q a ) P P P T T T T T T T T T T [ i ] T[i] T [ i ] P P P P j P_{j} P j P j P_{j} P j T i T_{i} T i q = ϕ ( T i ) q=\phi\left(T_{i}\right) q = ϕ ( T i ) T i T_{i} T i q q q δ \delta δ q q q P P P T i T_{i} T i q q q P q ⊐ T i P_{q} \sqsupset T_{i} P q ⊐ T i q = σ ( T i ) q=\sigma\left(T_{i}\right) q = σ ( T i ) q = m q=m q = m P P P m m m T i T_{i} T i ϕ ( T i ) \phi\left(T_{i}\right) ϕ ( T i ) σ ( T i ) \sigma\left(T_{i}\right) σ ( T i ) q q q 32.4 32.4 32.4
ϕ ( T i ) = σ ( T i ) \phi\left(T_{i}\right)=\sigma\left(T_{i}\right)
ϕ ( T i ) = σ ( T i )
如果自动机处在状态 q q q T [ i + 1 ] = a T[i+1]=a T [ i + 1 ] = a T i a T_{i} a T i a P P P σ ( T i a ) \sigma\left(T_{i} a\right) σ ( T i a ) P q P_{q} P q P P P T i T_{i} T i P P P T i a T_{i} a T i a σ ( T i a ) \sigma\left(T_{i} a\right) σ ( T i a ) σ ( P q a ) \sigma\left(P_{q} a\right) σ ( P q a ) 32.3 32.3 32.3 σ ( T i a ) = σ ( P q a ) ) \left.\sigma\left(T_{i} a\right)=\sigma\left(P_{q} a\right)\right) σ ( T i a ) = σ ( P q a ) ) q q q a a a σ ( P q a ) \sigma\left(P_{q} a\right) σ ( P q a )
考虑以下两种情况。第一种情况是, a = P [ q + 1 ] a=P[q+1] a = P [ q + 1 ] a a a δ ( q , a ) = q + 1 \delta(q, a)=q+1 δ ( q , a ) = q + 1 a ≠ P [ q + 1 ] a \neq P[q+1] a = P [ q + 1 ] a a a P P P T i T_{i} T i P P P
让我们看一个例子。图 32-7 的字符串匹配自动机有 δ ( 5 , c ) = 6 \delta(5, c)=6 δ ( 5 , c ) = 6 δ ( 5 , b ) = 4 \delta(5, b)=4 δ ( 5 , b ) = 4 q = 5 q=5 q = 5 b \mathrm{b} b P q b = a b a b a b P_{q} \mathrm{~b}=\mathrm{ababab} P q b = ababab P P P P 4 = a b a b P_{4}=\mathrm{abab} P 4 = abab
为了清楚说明字符串匹配自动机的操作过程, 我们给出一个简单而有效的程序, 用来模拟这样一个自动机(用它的转移函数 δ \delta δ T [ 1.. n ] T[1 . . n] T [ 1.. n ] m m m P P P m m m Q Q Q { 0 , 1 , ⋯ , m } \{0,1, \cdots, m\} { 0 , 1 , ⋯ , m } m m m
FINITE-AUTOMATON-MATCHER(T, δ ,m) 1 n = T length 2 q = 0 3 for i = 1 to n 4 q = δ ( q , T [ i ] ) 5 if q = = m 6 print “Pattern occurs with shift” i − m \begin{aligned}
&\text { FINITE-AUTOMATON-MATCHER(T,} \delta \text{,m) } \\
1 & \quad n=T \text { length } \\
2 & \quad q=0 \\
3 & \quad \text {for } i=1 \text { to } n \\
4 & \quad \quad q=\delta(q, T[i]) \\
5 & \quad \quad \text {if } q==m \\
6 & \quad \quad \quad \text {print “Pattern occurs with shift” } i-m
\end{aligned}
1 2 3 4 5 6 FINITE-AUTOMATON-MATCHER(T, δ ,m) n = T length q = 0 for i = 1 to n q = δ ( q , T [ i ]) if q == m print “Pattern occurs with shift” i − m
从 FINITE-AUTOMATON-MATCHER 的简单循环结构可以看出, 对于一个长度为 n n n Θ ( n ) \Theta(n) Θ ( n ) δ \delta δ
考察自动机在输入文本 T [ 1.. n ] T[1 . . n] T [ 1.. n ] T [ i ] T[i] T [ i ] σ ( T i ) \sigma\left(T_{i}\right) σ ( T i ) P ⊐ T i , σ ( T i ) = m P \sqsupset T_{i}, \sigma\left(T_{i}\right)=m P ⊐ T i , σ ( T i ) = m P P P m m m σ \sigma σ
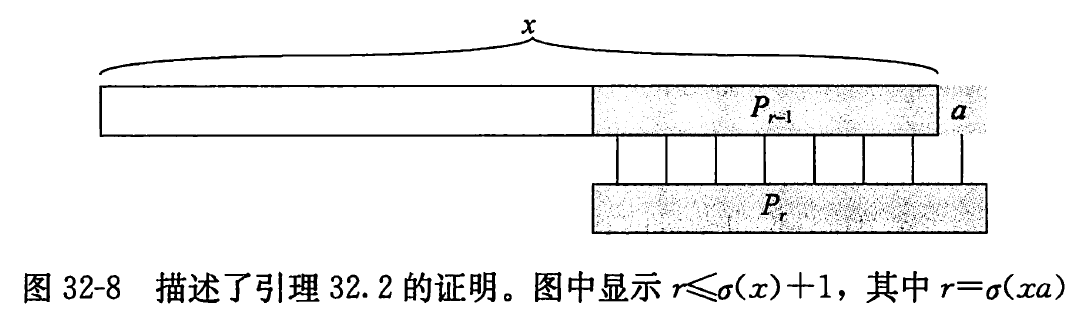
引理 32. 2(后缀函数不等式) 对任意字符串 x x x a , σ ( x a ) ⩽ σ ( x ) + 1 a, \sigma(x a) \leqslant \sigma(x)+1 a , σ ( x a ) ⩽ σ ( x ) + 1
证明 参照图 32-8, 设 r = σ ( x a ) r=\sigma(x a) r = σ ( x a ) r = 0 r=0 r = 0 σ ( x ) \sigma(x) σ ( x ) σ ( x a ) = r ⩽ σ ( x ) + 1 \sigma(x a)=r \leqslant \sigma(x)+1 σ ( x a ) = r ⩽ σ ( x ) + 1 r > 0 r>0 r > 0 σ \sigma σ P r ⊐ x a P_{r} \sqsupset x a P r ⊐ x a a a a P r P_{r} P r x a x a x a P r − 1 ⊐ x ∘ P_{r-1} \sqsupset x_{\circ} P r − 1 ⊐ x ∘ r − 1 ⩽ σ ( x ) r-1 \leqslant \sigma(x) r − 1 ⩽ σ ( x ) σ ( x ) \sigma(x) σ ( x ) P k ⊐ x P_{k} \sqsupset x P k ⊐ x k k k σ ( x a ) = r ⩽ σ ( x ) + 1 \sigma(x a)=r \leqslant \sigma(x)+1 σ ( x a ) = r ⩽ σ ( x ) + 1
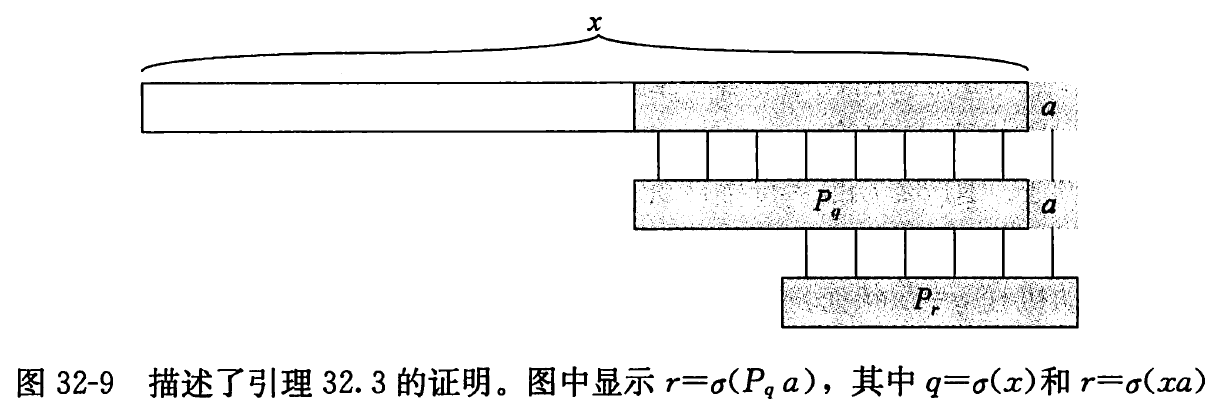
引理 32. 3(后缀函数递归引理) 对任意 x x x a a a q = σ ( x ) q=\sigma(x) q = σ ( x ) σ ( x a ) = σ ( P q a ) \sigma(x a)=\sigma\left(P_{q} a\right) σ ( x a ) = σ ( P q a )
证明 根据 σ \sigma σ P q ⊐ x P_{q} \sqsupset x P q ⊐ x P q a ⊐ x a P_{q} a \sqsupset x a P q a ⊐ x a r = σ ( x a ) r=\sigma(x a) r = σ ( x a ) P r ⊐ P_{r} \sqsupset P r ⊐ x a x a x a 32.2 32.2 32.2 r ⩽ q + 1 r \leqslant q+1 r ⩽ q + 1 ∣ P r ∣ = r ⩽ q + 1 = ∣ P q a ∣ \left|P_{r}\right|=r \leqslant q+1=\left|P_{q} a\right| ∣ P r ∣ = r ⩽ q + 1 = ∣ P q a ∣ P q a P_{q} a P q a x a x a x a P r ⊐ x a P_{r} \sqsupset x a P r ⊐ x a ∣ P r ∣ ⩽ ∣ P q a ∣ \left|P_{r}\right| \leqslant\left|P_{q} a\right| ∣ P r ∣ ⩽ ∣ P q a ∣ 32.1 32.1 32.1 P r ⊐ P q a P_{r} \sqsupset P_{q} a P r ⊐ P q a r ⩽ σ ( P q a ) r \leqslant \sigma\left(P_{q} a\right) r ⩽ σ ( P q a ) σ ( x a ) ⩽ σ ( P q a ) \sigma(x a) \leqslant \sigma\left(P_{q} a\right) σ ( x a ) ⩽ σ ( P q a ) P q a P_{q} a P q a x a x a x a σ ( P q a ) ⩽ σ ( x a ) \sigma\left(P_{q} a\right) \leqslant \sigma(x a) σ ( P q a ) ⩽ σ ( x a ) σ ( P q a ) = σ ( x a ) \sigma\left(P_{q} a\right)=\sigma(x a) σ ( P q a ) = σ ( x a )
现在我们就可以来证明用于描述字符串匹配自动机在给定输入文本上操作过程的主要定理 了。如上所述, 这个定理说明了自动机在每一步中仅仅记录所读入字符串后缀的最长前缀。换句话说, 自动机保持着不变式 (32.5)。
定理 32. 4 如果 ϕ \phi ϕ P P P T [ 1.. n ] T[1 . . n] T [ 1.. n ] i = 0 , 1 , ⋯ , n , ϕ ( T i ) = σ ( T i ) i=0,1, \cdots, n, \phi\left(T_{i}\right)=\sigma\left(T_{i}\right) i = 0 , 1 , ⋯ , n , ϕ ( T i ) = σ ( T i )
证明 对 i i i i = 0 i=0 i = 0 T 0 = ε T_{0}=\varepsilon T 0 = ε ϕ ( T 0 ) = 0 = σ ( T 0 ) \phi\left(T_{0}\right)=0=\sigma\left(T_{0}\right) ϕ ( T 0 ) = 0 = σ ( T 0 )
现在假设 ϕ ( T i ) = σ ( T i ) \phi\left(T_{i}\right)=\sigma\left(T_{i}\right) ϕ ( T i ) = σ ( T i ) ϕ ( T i + 1 ) = σ ( T i + 1 ) \phi\left(T_{i+1}\right)=\sigma\left(T_{i+1}\right) ϕ ( T i + 1 ) = σ ( T i + 1 ) q q q ϕ ( T i ) , a \phi\left(T_{i}\right), a ϕ ( T i ) , a T [ i + 1 ] T[i+1] T [ i + 1 ]
ϕ ( T i + 1 ) = ϕ ( T i a ) ( 根据 T i + 1 和 a 的定义 ) = δ ( ϕ ( T i ) , a ) ( 根据 ϕ 的定义 ) = δ ( q , a ) ( 根据 q 的定义 ) = σ ( P q a ) ( 根据式 ( 32.4 ) 关于 δ 的定义 ) = σ ( T i a ) ( 根据引理 32.3 和归纳假设 ) = σ ( T i + 1 ) ( 根据 T i + 1 的定义 ) \begin{aligned}
\phi\left(T_{i+1}\right) &=\phi\left(T_{i} a\right) &\left(\text { 根据 } T_{i+1} \text { 和 } a \text { 的定义 }\right) \\
&=\delta\left(\phi\left(T_{i}\right), a\right) &(\text { 根据 } \phi \text { 的定义 }) \\
&=\delta(q, a) &(\text { 根据 } q \text { 的定义 }) \\
&=\sigma\left(P_{q} a\right) &(\text { 根据式 }(32.4) \text { 关于 } \delta \text { 的定义 }) \\
&=\sigma\left(T_{i} a\right) &(\text { 根据引理 } 32.3 \text { 和归纳假设 }) \\
&=\sigma\left(T_{i+1}\right) &\left(\text { 根据 } T_{i+1} \text { 的定义 }\right)
\end{aligned}
ϕ ( T i + 1 ) = ϕ ( T i a ) = δ ( ϕ ( T i ) , a ) = δ ( q , a ) = σ ( P q a ) = σ ( T i a ) = σ ( T i + 1 ) ( 根据 T i + 1 和 a 的定义 ) ( 根据 ϕ 的定义 ) ( 根据 q 的定义 ) ( 根据式 ( 32.4 ) 关于 δ 的定义 ) ( 根据引理 32.3 和归纳假设 ) ( 根据 T i + 1 的定义 )
根据定理 32.4 32.4 32.4 q q q q q q P q ⊐ T i P_{q} \sqsupset T_{i} P q ⊐ T i q = m q=m q = m P P P
计算转移函数
下面的过程根据一个给定模式 P [ 1.. m ] P[1 . . m] P [ 1.. m ] δ ∘ \delta_{\circ} δ ∘
COMPUTE − TRANSITION-FUNCTION ( P , Σ ) 1 m = P . length 2 for q = 0 to m 3 for each charater a ∈ Σ 4 k = min ( m + 1 , q + 2 ) 5 repeat 6 k = k − 1 6 until P k ⊐ P q a 7 δ ( q , a ) = k 8 return δ \begin{aligned}
&\operatorname{COMPUTE}-\operatorname{TRANSITION-FUNCTION}(P, \Sigma) \\
&1 \quad m=P . \text { length } \\
&2 \quad \text {for } q=0 \text { to } m \\
&3 \quad \quad \text {for each charater } a \in \Sigma\\
&4 \quad \quad \quad k=\min (m+1, q+2)\\
&5 \quad \quad \quad \text {repeat }\\
&6 \quad \quad \quad \quad k=k-1\\
&6 \quad \quad \quad \text {until } P_{k} \sqsupset P_{q} a\\
&7 \quad \quad \quad \delta(q, a)=k\\
&8 \quad \text{return }\delta\\
\end{aligned}
COMPUTE − TRANSITION-FUNCTION ( P , Σ ) 1 m = P . length 2 for q = 0 to m 3 for each charater a ∈ Σ 4 k = min ( m + 1 , q + 2 ) 5 repeat 6 k = k − 1 6 until P k ⊐ P q a 7 δ ( q , a ) = k 8 return δ
这个过程根据在式 (32. 4) 中的定义直接计算 δ ( q , a ) \delta(q, a) δ ( q , a ) q q q a a a 4 ∼ 8 4 \sim 8 4 ∼ 8 δ ( q , a ) \delta(q, a) δ ( q , a ) P k ⊐ P q a P_{k} \sqsupset P_{q} a P k ⊐ P q a k k k k k k min ( m , q + 1 ) \min (m, q+1) min ( m , q + 1 ) k k k P k ⊐ P q a P_{k} \sqsupset P_{q} a P k ⊐ P q a P 0 = ε P_{0}=\varepsilon P 0 = ε
COMPUTE-TRANSITION-FUNCTION 的运行时间为 O ( m 3 ∣ Σ ∣ ) O\left(m^{3}|\Sigma|\right) O ( m 3 ∣Σ∣ ) m ∣ ∑ ∣ m\left|\sum\right| m ∣ ∑ ∣ m + l m+l m + l P k ⊐ P q a P_{k} \sqsupset P_{q} a P k ⊐ P q a m m m P P P P P P δ \delta δ O ( m ∣ Σ ∣ ) O(m|\Sigma|) O ( m ∣Σ∣ ) δ \delta δ Σ \Sigma Σ m m m n n n O ( m ∣ Σ ∣ ) O(m|\Sigma|) O ( m ∣Σ∣ ) Θ ( n ) \Theta(n) Θ ( n )
Knuth-Morris-Pratt 算法
现在来介绍一种由 Knuth、Morris 和 Pratt 三人设计的线性时间字符串匹配算法。这个算法无需计算转移函数 δ \delta δ Θ ( n ) \Theta(n) Θ ( n ) π \pi π Θ ( m ) \Theta(m) Θ ( m ) π [ 1.. m ] \pi[1 . . m] π [ 1.. m ] π \pi π δ ∘ \delta_{\circ} δ ∘ q = 0 , 1 , ⋯ , m q=0,1, \cdots, m q = 0 , 1 , ⋯ , m a ∈ Σ , π [ q ] a \in \Sigma, \pi[q] a ∈ Σ , π [ q ] a a a δ ( q , a ) \delta(q, a) δ ( q , a ) π \pi π m m m δ \delta δ Θ ( m ∣ ∑ ∣ ) \Theta\left(m\left|\sum\right|\right) Θ ( m ∣ ∑ ∣ ) π \pi π δ \delta δ Σ \Sigma Σ
关于模式的前缀函数
模式的前缀函数 π \pi π δ \delta δ
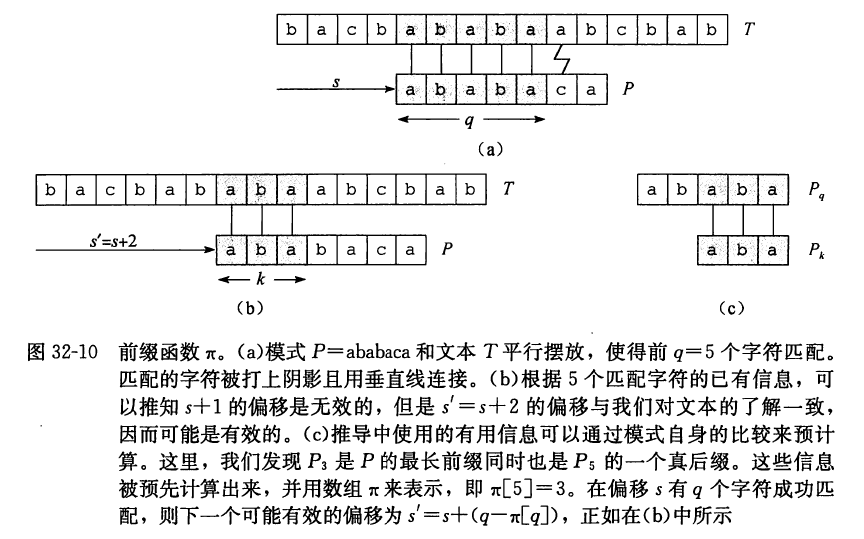
考察一下朴素字符串匹配算法的操作过程。图 32-10(a)展示了一个针对文本 T T T s s s P = a b a b a c a P=\mathrm{ababaca} P = ababaca q = 5 q=5 q = 5 q q q q q q s + 1 s+1 s + 1 s ′ = s + 2 s^{\prime}=s+2 s ′ = s + 2
假设模式字符 P [ 1.. q ] P[1 . . q] P [ 1.. q ] T [ s + 1.. s + q ] T[s+1 .. s+q] T [ s + 1.. s + q ] s ′ s^{\prime} s ′ s ′ > s s^{\prime}>s s ′ > s k < q k<q k < q
P [ 1 … k ] = T [ s ′ + 1 … s ′ + k ] ( 32.6 ) P[1 \ldots k]=T\left[s^{\prime}+1 \ldots s^{\prime}+k\right] \quad \quad (32.6)
P [ 1 … k ] = T [ s ′ + 1 … s ′ + k ] ( 32.6 )
的最小偏移 s ′ > s s^{\prime}>s s ′ > s s ′ + k = s + q s^{\prime}+k=s+q s ′ + k = s + q
换句话说, 已知 P q ⊐ T s + q P_{q} \sqsupset T_{s+q} P q ⊐ T s + q P q P_{q} P q P k P_{k} P k T s + q T_{s+q} T s + q s ′ + k = s^{\prime}+k= s ′ + k = s + q s+q s + q s s s q q q s ′ s^{\prime} s ′ k ∘ k_{\circ} k ∘ P P P q − k q-k q − k s s s s ′ s^{\prime} s ′ s ′ = s + ( q − k ) s^{\prime}=s+(q-k) s ′ = s + ( q − k ) k = 0 k=0 k = 0 s ′ = s + q s^{\prime}=s+q s ′ = s + q s + 1 , s + 2 , ⋯ , s + q − 1 s+1, s+2, \cdots, s+q-1 s + 1 , s + 2 , ⋯ , s + q − 1 s ′ s^{\prime} s ′ P P P k k k T T T
可以用模式与其自身进行比较来预先计算出这些必要的信息, 如图 32-10© 所示。由于 T [ s ′ + 1.. s ′ + k ] T\left[s^{\prime}+1 . . s^{\prime}+k\right] T [ s ′ + 1.. s ′ + k ] P q P_{q} P q P k ⊐ P q P_{k} \sqsupset P_{q} P k ⊐ P q k < q k<q k < q s ′ = s + ( q − k ) s^{\prime}=s+(q-k) s ′ = s + ( q − k ) q q q k k k s ′ s^{\prime} s ′ s ′ − s s^{\prime}-s s ′ − s
下面是预计算过程的形式化说明。已知一个模式 P [ 1 … m ] P[1 \ldots m] P [ 1 … m ] P P P π : { 1 , 2 , ⋯ , m } → { 0 , 1 , ⋯ , m − 1 } \pi:\{1,2, \cdots, m\} \rightarrow\{0,1, \cdots, m-1\} π : { 1 , 2 , ⋯ , m } → { 0 , 1 , ⋯ , m − 1 }
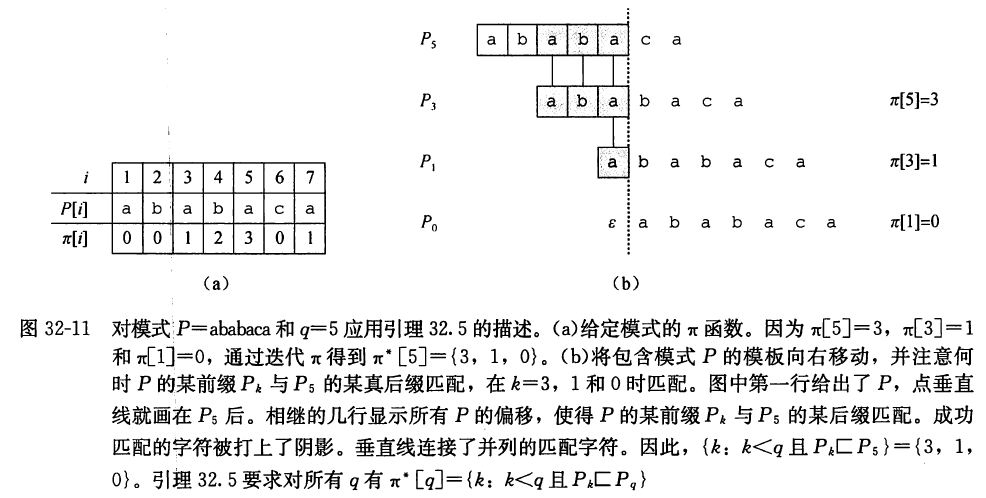
π [ q ] = max { k : k < q 且 P k ⊐ P q } \pi[q]=\max \left\{k: k<q \text { 且 } P_{k} \sqsupset P_{q}\right\}
π [ q ] = max { k : k < q 且 P k ⊐ P q }
即 π [ q ] \pi[q] π [ q ] P P P P q P_{q} P q π \pi π
伪代码及C++实现
下面给出的 Knuth-Morris-Pratt 匹配算法的伪代码就是 KMP-MATCHER 过程。我们将看到, 其大部分都是在模仿 FINITE-AUTOMATON-MATCHER。KMP-MATCHER 调用了一个辅助程序 COMPUTE-PREFIX-FUNCTION 来计算 π \pi π
KMP-MATCHER ( T , P ) 1 n = T . length 2 m = P . length 3 π = COMPUTE-PREFIX-FUNCTION ( P ) 4 q = 0 // number of characters matched 5 for i = 1 to n // scan the text from left to right 6 while q > 0 and P [ q + 1 ] ≠ T [ i ] // next character does not match 7 q = π [ q ] 8 if P [ q + 1 ] = = T [ i ] / / next character matches 9 q = q + 1 / / number of characters matched + 1 10 if q = = m / / is all of P matched? 11 print “Pattern occurs with shift” i − m 12 q = π [ q ] / / look for the next match COMPUTE-PREFIX-FUNCTION ( P ) 1 m = P . length 2 let π [ 1.. m ] be a new array 3 π [ 1 ] = 0 4 k = 0 5 for q = 2 to m 6 while k > 0 and P [ k + 1 ] ≠ P [ q ] 7 k = π [ k ] 8 if P [ k + 1 ] = = P [ q ] 9 k = k + 1 10 π [ q ] = k 11 return π \begin{aligned}
&\begin{array}{rl}
&\text {KMP-MATCHER}(T,P) \\
1 & n=T \text {. length } \\
2 & m=P \text {. length } \\
3 & \pi=\text { COMPUTE-PREFIX-FUNCTION }(P) \\
4 & q=0 & \text {// number of characters matched }\\
5 & \text {for } i=1 \text { to } n &\text {// scan the text from left to right }\\
6 & \quad \text {while } q>0 \text { and } P[q+1] \neq T[i] & \text {// next character does not match }\\
7 & \quad \quad q=\pi[q] & \\
8 & \quad \text {if } P[q+1]==T[i] & // \text { next character matches }\\
9 & \quad \quad q=q+1 & // \text { number of characters matched + 1 } \\
10 & \quad \text {if } q==m & // \text { is all of } P \text { matched? } \\
11 & \quad \quad \text {print “Pattern occurs with shift” } i-m & \\
12 & \quad \quad q=\pi[q] & // \text { look for the next match }\\
\\
&\text {COMPUTE-PREFIX-FUNCTION }(P) \\
1 & m=P \text {. length } \\
2 & \text {let } \pi[1 . . m] \text { be a new array } \\
3 & \pi[1]=0 \\
4 & k=0 \\
5 & \text {for } q=2 \text { to } m \\
6 & \quad \text {while } k>0 \text { and } P[k+1] \neq P[q] \\
7 & \quad \quad k=\pi[k] \\
8 & \quad \text {if } P[k+1]==P[q] \\
9 & \quad \quad k=k+1 \\
10 & \quad \pi[q]=k \\
11 & \text {return } \pi
\end{array}
\end{aligned}
1 2 3 4 5 6 7 8 9 10 11 12 1 2 3 4 5 6 7 8 9 10 11 KMP-MATCHER ( T , P ) n = T . length m = P . length π = COMPUTE-PREFIX-FUNCTION ( P ) q = 0 for i = 1 to n while q > 0 and P [ q + 1 ] = T [ i ] q = π [ q ] if P [ q + 1 ] == T [ i ] q = q + 1 if q == m print “Pattern occurs with shift” i − m q = π [ q ] COMPUTE-PREFIX-FUNCTION ( P ) m = P . length let π [ 1.. m ] be a new array π [ 1 ] = 0 k = 0 for q = 2 to m while k > 0 and P [ k + 1 ] = P [ q ] k = π [ k ] if P [ k + 1 ] == P [ q ] k = k + 1 π [ q ] = k return π // number of characters matched // scan the text from left to right // next character does not match // next character matches // number of characters matched + 1 // is all of P matched? // look for the next match
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 ne[1 ] = 0 ; for (int i = 2 , j = 0 ; i <= m; ++i) { while (j && p[i] != p[j + 1 ]) j = ne[j]; if (p[i] == p[j + 1 ]) ++j; ne[i] = j; } for (int i = 1 , j = 0 ; i <= n; ++i){ while (j && s[i] != p[j + 1 ]) j = ne[j]; if (s[i] == p[j + 1 ]) ++j; if (j == m) { j = ne[j]; } }
这两个程序有很多相似之处, 因为它们都是一个字符串针对模式 P P P T T T P P P P P P
下面先来分析这两个过程的运行时间, 对其正确性的证明要复杂一些。
运行时间分析
运用摊还分析的聚合方法 (参见 17.1 17.1 17.1 Θ ( m ) \Theta(m) Θ ( m ) 6 ∼ 7 6 \sim 7 6 ∼ 7 O ( m ) O(m) O ( m ) m − 1 m-1 m − 1 k k k k k k k k k 5 ∼ 10 5 \sim 10 5 ∼ 10 k k k m − 1 m-1 m − 1 k < q k<q k < q q q q k < q k<q k < q π [ q ] < q \pi[q]<q π [ q ] < q q = 1 , 2 , ⋯ , m q=1,2, \cdots, m q = 1 , 2 , ⋯ , m k k k k k k k k k k k k k k k m − 1 m-1 m − 1 m − 1 m-1 m − 1 Θ ( m ) \Theta(m) Θ ( m )
练习 32. 4-4 要求读者通过运用类似的聚合分析, 证明 KMP-MATCHER 的匹配时间 为 Θ ( n ) \Theta(n) Θ ( n )
与 FINITE-AUTOMATON-MATCHER 相比, 通过运用 π \pi π δ \delta δ O ( m ∣ Σ ∣ ) O(m|\Sigma|) O ( m ∣Σ∣ ) Θ ( m ) \Theta(m) Θ ( m ) Θ ( n ) \Theta(n) Θ ( n )
前缀函数计算的正确性
我们稍后就会看到, 前缀函数 π \pi π δ \delta δ P k P_{k} P k P q P_{q} P q π [ q ] \pi[q] π [ q ] π \pi π P q P_{q} P q P k P_{k} P k
π ∗ [ q ] = { π [ q ] , π ( 2 ) [ q ] , π ( 3 ) [ q ] , ⋯ , π ( t ) [ q ] } \pi^{\ast}[q]=\left\{\pi[q], \pi^{(2)}[q], \pi^{(3)}[q], \cdots, \pi^{(t)}[q]\right\}
π ∗ [ q ] = { π [ q ] , π ( 2 ) [ q ] , π ( 3 ) [ q ] , ⋯ , π ( t ) [ q ] }
其中 π ( i ) [ q ] \pi^{(i)}[q] π ( i ) [ q ] π ( 0 ) [ q ] = q \pi^{(0)}[q]=q π ( 0 ) [ q ] = q i ⩾ 1 , π ( i ) [ q ] = π [ π ( i − 1 ) [ q ] ] i \geqslant 1, \pi^{(i)}[q]=\pi\left[\pi^{(i-1)}[q]\right] i ⩾ 1 , π ( i ) [ q ] = π [ π ( i − 1 ) [ q ] ] π ( t ) [ q ] = 0 \pi^{(t)}[q]=0 π ( t ) [ q ] = 0 π ∗ [ q ] \pi^{\ast}[q] π ∗ [ q ]
引理 32. 5(前缀函数迭代引理) 设 P P P m m m π \pi π q = 1 , 2 , ⋯ , m q=1,2, \cdots, m q = 1 , 2 , ⋯ , m π ∗ [ q ] = { k : k < q \pi^{\ast}[q]=\left\{k: k<q\right. π ∗ [ q ] = { k : k < q P k ] P q } \left.\left.P_{k}\right] P_{q}\right\} P k ] P q }
证明 首先证明 π ∗ [ q ] ⊆ { k : k < q \pi^{\ast}[q] \subseteq\left\{k: k<q\right. π ∗ [ q ] ⊆ { k : k < q P k ] P q } \left.\left.P_{k}\right] P_{q}\right\} P k ] P q }
i ∈ π ∗ [ q ] 蕴涵着 P i ⊐ P q i \in \pi^{*}[q] \text { 蕴涵着 } P_{i} \sqsupset P_{q}
i ∈ π ∗ [ q ] 蕴涵着 P i ⊐ P q
若 i ∈ π ∗ [ q ] i \in \pi^{\ast}[q] i ∈ π ∗ [ q ] u > 0 u>0 u > 0 i = π ( u ) [ q ] i=\pi^{(u)}[q] i = π ( u ) [ q ] u u u u = 1 u=1 u = 1 i = π [ q ] i=\pi[q] i = π [ q ] π \pi π i < q i<q i < q P π [ q ] ⊐ P q P_{\pi [q]} \sqsupset P_{q} P π [ q ] ⊐ P q π [ i ] < i \pi[i]<i π [ i ] < i P π [ i ] ⊐ P i P_{\pi[i]} \sqsupset P_i P π [ i ] ⊐ P i < < < ⊐ \sqsupset ⊐ i ∈ π ∗ [ q ] i \in \pi^{\ast}[q] i ∈ π ∗ [ q ] π ∗ [ q ] ⊆ { k : k < q 且 P k ⊐ P q } \pi^{\ast}[q] \subseteq \{ k: \; k<q \text{ 且 } P_{k} \sqsupset P_{q} \} π ∗ [ q ] ⊆ { k : k < q 且 P k ⊐ P q }
下面用反证法来证明 { k : k < q \left\{k: k<q\right. { k : k < q P k ⊐ P q } ⊆ π ∗ [ q ] \left.P_{k} \sqsupset P_{q}\right\} \subseteq \pi^{\ast}[q] P k ⊐ P q } ⊆ π ∗ [ q ] { k : k < q \left\{k: k<q\right. { k : k < q P k ⊐ P q } − π ∗ [ q ] \left.P_{k} \sqsupset P_{q}\right\}-\pi^{\ast}[q] P k ⊐ P q } − π ∗ [ q ] j j j π [ q ] \pi[q] π [ q ] { k : k < q \left\{k: k<q\right. { k : k < q P k ⊐ P q } \left.P_{k} \sqsupset P_{q}\right\} P k ⊐ P q } π [ q ] ∈ π ∗ [ q ] \pi[q] \in \pi^{\ast}[q] π [ q ] ∈ π ∗ [ q ] j < π [ q ] j<\pi[q] j < π [ q ] j ′ j^{\prime} j ′ π ∗ [ q ] \pi^{\ast}[q] π ∗ [ q ] j j j π ∗ [ q ] \pi^{\ast}[q] π ∗ [ q ] j j j j ′ = π [ q ] j^{\prime}=\pi[q] j ′ = π [ q ] P j ⊐ P q P_{j} \sqsupset P_{q} P j ⊐ P q j ∈ { k : k < q j \in\left\{k: k<q\right. j ∈ { k : k < q P k ⊐ P q } \left.P_{k} \sqsupset P_{q}\right\} P k ⊐ P q } j ′ ∈ π ∗ [ q ] j^{\prime} \in \pi^{\ast}[q] j ′ ∈ π ∗ [ q ] P j ′ ⊐ P q P_{j^{\prime}} \sqsupset P_{q} P j ′ ⊐ P q 32.1 , P j ⊐ P j ′ 32.1, P_{j} \sqsupset P_{j^{\prime}} 32.1 , P j ⊐ P j ′ j j j j ′ j^{\prime} j ′ π [ j ′ ] = j \pi\left[j^{\prime}\right]=j π [ j ′ ] = j j ′ ∈ π ∗ [ q ] j^{\prime} \in \pi^{\ast}[q] j ′ ∈ π ∗ [ q ] j ∈ π ∗ [ q ] j \in \pi^{\ast}[q] j ∈ π ∗ [ q ]
算法 COMPUTE-PREFIX-FUNCTION 根据 q = 1 , 2 , ⋯ , m q=1,2, \cdots, m q = 1 , 2 , ⋯ , m π [ q ] \pi[q] π [ q ] π [ 1 ] = 0 \pi[1]=0 π [ 1 ] = 0 q q q π [ q ] < q \pi[q] \lt q π [ q ] < q q > 1 q \gt 1 q > 1 π [ q ] \pi[q] π [ q ]
引理 32.6 32.6 32.6 设 P P P m m m π \pi π P P P q = 1 , 2 , ⋯ , m q=1,2, \cdots, m q = 1 , 2 , ⋯ , m π [ q ] > 0 \pi[q]>0 π [ q ] > 0 π [ q ] − 1 ∈ π ∗ [ q − 1 ] \pi[q]-1 \in \pi^{\ast}[q-1] π [ q ] − 1 ∈ π ∗ [ q − 1 ]
证明
如果 r = π [ q ] > 0 r=\pi[q]\gt 0 r = π [ q ] > 0 r < q 且 P r ⊐ P q r \lt q \text{ 且 }P_r \sqsupset P_q r < q 且 P r ⊐ P q
因此 r − 1 < q − 1 且 P r − 1 ⊐ P q − 1 r-1\lt q-1 \text{ 且 } P_{r-1} \sqsupset P_{q-1} r − 1 < q − 1 且 P r − 1 ⊐ P q − 1
(把 P r P_r P r P q P_q P q r > 0 r \gt 0 r > 0
因此, 根据引理 32.5,r − 1 ∈ π ∗ [ q − 1 ] r-1 \in \pi^{\ast}[q-1] r − 1 ∈ π ∗ [ q − 1 ]
因此 π [ q ] − 1 = r − 1 ∈ π ∗ [ q − 1 ] \pi[q]-1=r-1 \in \pi^{\ast}[q-1] π [ q ] − 1 = r − 1 ∈ π ∗ [ q − 1 ]
对 q = 2 , 3 , ⋯ , m q=2,3, \cdots, m q = 2 , 3 , ⋯ , m E q − 1 ⊆ π ∗ [ q − 1 ] E_{q-1} \subseteq \pi^{\ast}[q-1] E q − 1 ⊆ π ∗ [ q − 1 ]
E q − 1 = ( k ∈ π ∗ [ q − 1 ] : P [ k + 1 ] = P [ q ] } = { k : k < q − 1 , P k ⊐ P q − 1 , P [ k + 1 ] = P [ q ] } (根据引理 32.5) = { k : k < q − 1 , P k + 1 ⊐ P q } \begin{aligned}
E_{q-1} &=\left(k \in \pi^{\ast}[q-1]: P[k+1]=P[q]\right\} \\
&=\left\{k: k<q-1, P_{k} \sqsupset P_{q-1}, P[k+1]=P[q]\right\} \quad \text { (根据引理 32.5) } \\
&=\left\{k: k<q-1, P_{k+1} \sqsupset P_{q}\right\}
\end{aligned}
E q − 1 = ( k ∈ π ∗ [ q − 1 ] : P [ k + 1 ] = P [ q ] } = { k : k < q − 1 , P k ⊐ P q − 1 , P [ k + 1 ] = P [ q ] } (根据引理 32.5 ) = { k : k < q − 1 , P k + 1 ⊐ P q }
集合 E q − 1 E_{q-1} E q − 1 P k ] P q − 1 \left.P_{k}\right] P_{q-1} P k ] P q − 1 P [ k + 1 ] = P [ q ] P[k+1]=P[q] P [ k + 1 ] = P [ q ] k < q − 1 k<q-1 k < q − 1 P [ k + 1 ] = P [ q ] P[k+1]=P[q] P [ k + 1 ] = P [ q ] P k + 1 ⊐ P q P_{k+1}\sqsupset P_{q} P k + 1 ⊐ P q E q − 1 E_{q-1} E q − 1 k ∈ π ∗ [ q − 1 ] k \in \pi^{\ast}[q-1] k ∈ π ∗ [ q − 1 ] P k P_{k} P k P k + 1 P_{k+1} P k + 1 P q P_{q} P q
推论 32.7 32.7 32.7 设 P P P m m m π \pi π P P P q = 2 , 3 , ⋯ , m q=2,3, \cdots, m q = 2 , 3 , ⋯ , m
π [ q ] = { 0 如果 E q − 1 = ∅ 1 + max { k ∈ E q − 1 } 如果 E q − 1 ≠ ∅ \pi[q]= \begin{cases}0 & \text { 如果 } E_{q-1}=\varnothing \\ 1+\max \left\{k \in E_{q-1}\right\} & \text { 如果 } E_{q-1} \neq \varnothing\end{cases}
π [ q ] = { 0 1 + max { k ∈ E q − 1 } 如果 E q − 1 = ∅ 如果 E q − 1 = ∅
证明 如果 E q − 1 E_{q-1} E q − 1 P k P_{k} P k P k + 1 P_{k+1} P k + 1 P q P_{q} P q k ∈ π ∗ [ q − 1 ] k \in \pi^{\ast}[q-1] k ∈ π ∗ [ q − 1 ] k = 0 k=0 k = 0 π [ q ] = 0 \pi[q]=0 π [ q ] = 0
如果 E q − 1 E_{q-1} E q − 1 k ∈ E q − 1 k \in E_{q-1} k ∈ E q − 1 k + 1 < q k+1<q k + 1 < q P k + 1 ⊐ P q P_{k+1} \sqsupset P_{q} P k + 1 ⊐ P q π [ q ] \pi[q] π [ q ]
π [ q ] ⩾ 1 + max { k ∈ E q − 1 } \pi[q] \geqslant 1+\max \left\{k \in E_{q-1}\right\}
π [ q ] ⩾ 1 + max { k ∈ E q − 1 }
注意到 π [ q ] > 0 \pi[q]>0 π [ q ] > 0 r = π [ q ] − 1 r=\pi[q]-1 r = π [ q ] − 1 r + 1 = π [ q ] r+1=\pi[q] r + 1 = π [ q ] P r + 1 ] P q \left.P_{r+1}\right] P_{q} P r + 1 ] P q r + 1 > 0 r+1>0 r + 1 > 0 P [ r + 1 ] = P [ q ] P[r+1]=P[q] P [ r + 1 ] = P [ q ] 32.6 32.6 32.6 r ∈ π ∗ [ q − 1 ] r \in \pi^{\ast}[q-1] r ∈ π ∗ [ q − 1 ] r ∈ E q − 1 r \in E_{q-1} r ∈ E q − 1 r ⩽ max { k ∈ r \leqslant \max \{k \in r ⩽ max { k ∈ E q − 1 } \left.E_{q-1}\right\} E q − 1 }
π [ q ] ⩽ 1 + max { k ∈ E q − 1 ) } \left.\pi[q] \leqslant 1+\max \left\{k \in E_{q-1}\right)\right\}
π [ q ] ⩽ 1 + max { k ∈ E q − 1 ) }
联合等式 (32.8) 和式 (32. 9) 即可完成证明。
现在来完成对 COMPUTE-PREFIX-FUNCTION 计算的 π \pi π 5 ∼ 10 5 \sim 10 5 ∼ 10 k = π [ q − 1 ] k=\pi[q-1] k = π [ q − 1 ] 6 ∼ 9 6 \sim 9 6 ∼ 9 k k k π [ q ] \pi[q] π [ q ] 6 ∼ 7 6 \sim 7 6 ∼ 7 k ∈ π ∗ [ q − 1 ] k \in \pi^{\ast}[q-1] k ∈ π ∗ [ q − 1 ] k k k P [ k + 1 ] = P [ q ] P[k+1]=P[q] P [ k + 1 ] = P [ q ] k k k E q − 1 E_{q-1} E q − 1 32.7 32.7 32.7 π [ q ] \pi[q] π [ q ] k + 1 k+1 k + 1 k = 0 k=0 k = 0 P [ 1 ] = P [ q ] P[1]=P[q] P [ 1 ] = P [ q ] k k k π [ q ] \pi[q] π [ q ] π [ q ] \pi[q] π [ q ] k ∘ k_{\circ} k ∘ 8 ∼ 10 8 \sim 10 8 ∼ 10 k k k π [ q ] \pi[q] π [ q ]
KMP算法的正确性
过程 KMP-MATCHER 可以看做是过程 FINITE-AUTOMATON-MATCHER 的一次重新实现, 但是却用到了前缀函数 π \pi π i i i m m m q q q
在我们正式证明 KMP-MATCHER 模仿 FINITE-AUTOMATON-MATCHER 之前, 让我们来理解前缀函数 π \pi π δ \delta δ q q q a = T [ i ] a=T[i] a = T [ i ] δ ( q , a ) \delta(q, a) δ ( q , a ) a = P [ q + 1 ] a=P[q+1] a = P [ q + 1 ] a a a δ ( q , a ) = q + 1 \delta(q, a)=q+1 δ ( q , a ) = q + 1 a ≠ P [ q + 1 ] a \neq P[q+1] a = P [ q + 1 ] a a a 0 ⩽ δ ( q , a ) 0 \leqslant \delta(q, a) 0 ⩽ δ ( q , a ) ⩽ q \leqslant q ⩽ q a a a q + 1 q+1 q + 1 π \pi π q q q
当 a a a π \pi π δ ( q , a ) \delta(q, a) δ ( q , a ) q q q q q q 6 ∼ 7 6 \sim 7 6 ∼ 7 π ∗ [ q ] \pi^{\ast}[q] π ∗ [ q ] q ′ q^{\prime} q ′ a a a P [ q ′ + 1 ] P\left[q^{\prime}+1\right] P [ q ′ + 1 ] q ′ q^{\prime} q ′ a a a P [ q ′ + 1 ] P\left[q^{\prime}+1\right] P [ q ′ + 1 ] q ′ + 1 q^{\prime}+1 q ′ + 1 δ ( q , a ) \delta(q, a) δ ( q , a ) δ ( q , a ) \delta(q, a) δ ( q , a ) π ∗ [ q ] \pi^{\ast}[q] π ∗ [ q ]
让我们来考虑图 32-7 和图 32-11 中的例子, 其中模式为 P = a b a b a c a P=\mathrm{ababaca} P = ababaca q = 5 q=5 q = 5 π ∗ [ 5 ] \pi^{\ast}[5] π ∗ [ 5 ] c c c δ ( 5 , c ) = 6 \delta(5, c)=6 δ ( 5 , c ) = 6 δ ( 5 , b ) = 4 \delta(5, \mathrm{~b})=4 δ ( 5 , b ) = 4 q ′ = π [ 5 ] = 3 q^{\prime}=\pi[5]=3 q ′ = π [ 5 ] = 3 P [ q ′ + 1 ] = P [ 4 ] = b P\left[q^{\prime}+1\right]=P[4]=\mathrm{b} P [ q ′ + 1 ] = P [ 4 ] = b q ′ + 1 = 4 = δ ( 5 , b ) q^{\prime}+1=4=\delta(5, \mathrm{~b}) q ′ + 1 = 4 = δ ( 5 , b ) a \mathrm{a} a δ ( 5 , a ) = 1 \delta(5,a)=1 δ ( 5 , a ) = 1 P [ 6 ] = c ≠ a P[6]=\mathrm{c} \neq \mathrm{a} P [ 6 ] = c = a π [ 5 ] = 3 \pi[5]=3 π [ 5 ] = 3 π ∗ [ 5 ] \pi^{\ast}[5] π ∗ [ 5 ] P [ 4 ] = b ≠ a P[4]=\mathrm{b} \neq \mathrm{a} P [ 4 ] = b = a π [ 3 ] = 1 \pi[3]=1 π [ 3 ] = 1 π ∗ [ 5 ] \pi^{\ast}[5] π ∗ [ 5 ] P [ 2 ] = b ≠ a P[2]=\mathrm{b} \neq \mathrm{a} P [ 2 ] = b = a π [ 1 ] = 0 \pi[1]=0 π [ 1 ] = 0 π ∗ [ 5 ] \pi^{\ast}[5] π ∗ [ 5 ] q ′ = 0 q^{\prime}=0 q ′ = 0 P [ q ′ + 1 ] = P [ 1 ] = a P\left[q^{\prime}+1\right]=P[1]=\mathrm{a} P [ q ′ + 1 ] = P [ 1 ] = a q ′ + 1 = 1 = δ ( 5 , a ) q^{\prime}+1=1=\delta(5, \mathrm{a}) q ′ + 1 = 1 = δ ( 5 , a )
因此, 我们了解到 KMP-MATCHER 通过以递减的顺序在状态 π ∗ [ q ] \pi^{\ast}[q] π ∗ [ q ] q ′ q^{\prime} q ′ q ′ + 1 q^{\prime}+1 q ′ + 1 δ ( q \delta(q δ ( q
我们现在准备正式证明 Knuth-Morris-Pratt 算法的正确性。根据定理 32.4, 在每次运行 FINITE-AUTOMATON-MATCHER 的第 4 行时得到 q = σ ( T i ) q=\sigma\left(T_{i}\right) q = σ ( T i ) q = 0 q=0 q = 0 i i i q ′ q^{\prime} q ′ q ′ = σ ( T i − 1 ) q^{\prime}=\sigma\left(T_{i-1}\right) q ′ = σ ( T i − 1 ) q = σ ( T i ) q=\sigma\left(T_{i}\right) q = σ ( T i ) ) ) )
当考虑到字符 T [ i ] T[i] T [ i ] P P P T i T_{i} T i P q ′ + 1 P_{q^{\prime}+1} P q ′ + 1 P [ q ′ + 1 ] = T [ i ] P\left[q^{\prime}+1\right]=T[i] P [ q ′ + 1 ] = T [ i ] P q ′ P_{q^{\prime}} P q ′ σ ( T i ) = 0 , σ ( T i ) = q ′ + 1 \sigma\left(T_{i}\right)=0, \sigma\left(T_{i}\right)=q^{\prime}+1 σ ( T i ) = 0 , σ ( T i ) = q ′ + 1 0 < σ ( T i ) ⩽ q ′ 0<\sigma\left(T_{i}\right) \leqslant q^{\prime} 0 < σ ( T i ) ⩽ q ′
如果 σ ( T i ) = 0 \sigma\left(T_{i}\right)=0 σ ( T i ) = 0 P 0 = ε P_{0}=\varepsilon P 0 = ε P P P T i T_{i} T i 6 ∼ 7 6 \sim 7 6 ∼ 7 π ∗ [ q ′ ] \pi^{\ast}\left[q^{\prime}\right] π ∗ [ q ′ ] P q ⊐ T i − 1 P_{q} \sqsupset T_{i-1} P q ⊐ T i − 1 q ∈ π ∗ [ q ′ ] q \in \pi^{\ast}\left[q^{\prime}\right] q ∈ π ∗ [ q ′ ] P [ q + 1 ] = T [ i ] P[q+1]=T[i] P [ q + 1 ] = T [ i ] q q q q = 0 q=0 q = 0 q = 0 q=0 q = 0 q = σ ( T i ) q=\sigma\left(T_{i}\right) q = σ ( T i )
如果 σ ( T i ) = q ′ + 1 \sigma\left(T_{i}\right)=q^{\prime}+1 σ ( T i ) = q ′ + 1 P [ q ′ + 1 ] = T [ i ] P\left[q^{\prime}+1\right]=T[i] P [ q ′ + 1 ] = T [ i ] q q q q = q ′ + 1 = σ ( T i ) q=q^{\prime}+1=\sigma\left(T_{i}\right) q = q ′ + 1 = σ ( T i )
如果 0 < σ ( T i ) ⩽ q ′ 0<\sigma\left(T_{i}\right) \leqslant q^{\prime} 0 < σ ( T i ) ⩽ q ′ 6 ∼ 7 6 \sim 7 6 ∼ 7 q ∈ π ∗ [ q ] q \in \pi^{\ast}[q] q ∈ π ∗ [ q ] q < q ′ q<q^{\prime} q < q ′ P q P_{q} P q P q P_{q} P q P [ q + 1 ] = T [ i ] P[q+1]=T[i] P [ q + 1 ] = T [ i ] q + 1 = σ ( P q ′ T [ i ] ) q+1=\sigma\left(P_{q^{\prime}} T[i]\right) q + 1 = σ ( P q ′ T [ i ] ) q ′ = σ ( T i − 1 ) q^{\prime}=\sigma\left(T_{i-1}\right) q ′ = σ ( T i − 1 ) 32.3 32.3 32.3 σ ( T i − 1 T [ i ] ) = σ ( P q ′ T [ i ] ) \sigma\left(T_{i-1} T[i]\right)=\sigma\left(P_{q^{\prime}} T[i]\right) σ ( T i − 1 T [ i ] ) = σ ( P q ′ T [ i ] )
q + 1 = σ ( P q ′ T [ i ] ) = σ ( T i − 1 T [ i ] ) = σ ( T i ) q+1=\sigma\left(P_{q^{\prime}} T[i]\right)=\sigma\left(T_{i-1} T[i]\right)=\sigma\left(T_{i}\right)
q + 1 = σ ( P q ′ T [ i ] ) = σ ( T i − 1 T [ i ] ) = σ ( T i )
当 while 循环终止时, 在第 9 行的 q q q q = σ ( T i ) q=\sigma\left(T_{i}\right) q = σ ( T i )
在 KMP-MATCHER 中, 之所以一定要有第 12 行代码, 是为了避免在找出 P P P P [ m + 1 ] P[m+1] P [ m + 1 ] a ∈ ∑ , δ ( m , a ) = a \in \sum, \delta(m, a)= a ∈ ∑ , δ ( m , a ) = δ ( π [ m ] , a ) \delta(\pi[m], a) δ ( π [ m ] , a ) δ ( P a ) = δ ( P π m ] a ) \delta(P a)=\delta\left(P_{\pi m]} a\right) δ ( P a ) = δ ( P πm ] a ) q = q= q = σ ( T i − 1 ) \sigma\left(T_{i-1}\right) σ ( T i − 1 ) ) ) )
综合运用
题目描述
你现在需要设计一个密码 S S S S S S
S S S N N N S S S S S S T T T
例如:a b c abc ab c a b c d e abcde ab c d e a b c d e abcde ab c d e a b d abd ab d a b c d e abcde ab c d e
请问共有多少种不同的密码满足要求?
由于答案会非常大,请输出答案模 1 0 9 + 7 10^9+7 1 0 9 + 7
输入格式
第一行输入整数N,表示密码的长度。
第二行输入字符串T,T中只包含小写字母。
输出格式
输出一个正整数 ,表示总方案数模 1 0 9 + 7 10^9+7 1 0 9 + 7
数据范围
1 ≤ N ≤ 50 1 \le N \le 50 1 ≤ N ≤ 50 1 ≤ ∣ T ∣ ≤ N 1 \le |T| \le N 1 ≤ ∣ T ∣ ≤ N ∣ T ∣ |T| ∣ T ∣ T T T
输入样例 1:
输出样例 1:
输入样例 2:
输出样例 2:
算法分析
f[i][j]:生成了 i个密码,且状态停留在 j,即有限自动机读入了 i个字符,且ϕ ( T i ) = j \phi(T_i)=j ϕ ( T i ) = j
状态 j也表示已成功匹配 j个字符
算法流程:
循环生成密码字符个数,正在生成第 i个字符
枚举生成 i - 1个密码字符后,所停留的状态 ϕ ( T i − 1 ) = j \phi(T_{i-1})=j ϕ ( T i − 1 ) = j
枚举正在生成的是什么字符,T [ i ] = a ∼ z T[i] = a \sim z T [ i ] = a ∼ z
计算状态转移,求 ϕ ( T i ) = δ ( j , T [ i ] ) \phi(T_i) = \delta(j,T[i]) ϕ ( T i ) = δ ( j , T [ i ]) π ( ) \pi() π ( )
状态转移从 j到 q,更新计算 f[i][q]的方案数
计算最终所有方案数,生成完 n个密码字符,且状态不停留在 m的方案都满足条件,累加起来
Solution
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 #include <iostream> using namespace std;const int N = 60 , mod = 1e9 + 7 ;int f[N][N], ne[N];int main () int n; cin >> n; string p; cin >> p; int m = p.size (); p = " " + p; for (int i = 2 , j = 0 ; i <= m; ++i) { while (j > 0 && p[i] != p[j + 1 ]) j = ne[j]; if (p[i] == p[j + 1 ]) ++j; ne[i] = j; } f[0 ][0 ] = 1 ; for (int i = 1 ; i <= n; ++i) { for (int j = 0 ; j < m; ++j) { for (char c = 'a' ; c <= 'z' ; ++c) { int q = j; while (q > 0 && c != p[q + 1 ]) q = ne[q]; if (c == p[q + 1 ]) ++q; if (q < m) f[i][q] = (f[i][q] + f[i - 1 ][j]) % mod; } } } int ans = 0 ; for (int j = 0 ; j < m; ++j) ans = (ans + f[n][j]) % mod; cout << ans; }