离散数学 | Dilworth定理

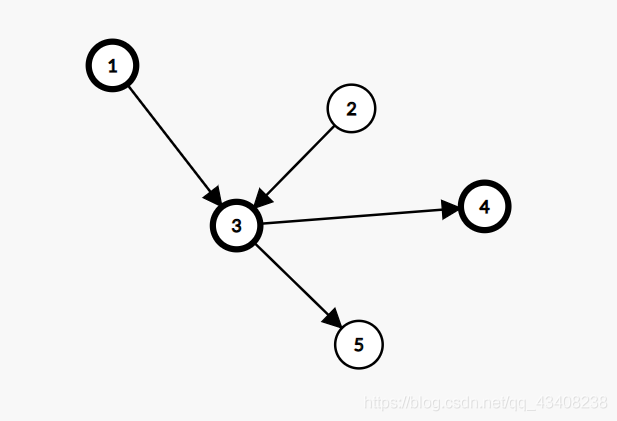
传递闭包

对于某个集合 $S$ 我们有定义在集合上的二元关系 $R$。

我们在 $S$ 上还定义了一个二元关系 $T$，若关系 $T$ 满足 $\forall x,y\in S$，$xTy\to{\exists} x_0=x,x_1,x_2,\dots,x_k=y$ 使得 $x_iRx_{i+1}(0\leq i<k)$ 均成立，那么就称关系 $T$ 为关系 $R$ 的传递闭包。

显然对于图 $G=(V,E)$，若我们把 $S$ 视作 $G$ 的点集 $V$，对于 $x,y\in V$，$xRy$ 为真当且仅当存在 $x\to y$ 的边，那么 $R$ 的传递闭包 $T$ 定义为：$xTy$ 为真当且仅当存在 $x\to y$ 的路径。

求传递闭包的方式非常容易，直接 $n^3$ 跑遍 floyd 就行了。

偏序关系

对于集合 $A$，若定义在集合 $A$ 上的关系 $R$ 满足：

• 自反性，$\forall x\in A$ 都有 $xRx$
• 反对称性，$\forall x,y\in A$，若 $xRy,yRx$ 则 $x=y$
• 传递性，$\forall x,y,z\in A$，若 $xRy,yRz$ 则 $xRz$

则称 $R$ 为定义在 $A$ 上的非严格偏序关系，记作 $\preccurlyeq$，可以把它理解为小于等于，但又不等于传统意义上的小于等于。

同理我们这样定义严格偏序，对于集合 $A$，若定义在集合 $A$ 上的关系 $R$ 满足：

• 反自反性，$\forall x\in A$，$xRx$ 都不成立
• 非对称性，$\forall x,y\in A$， $xRy$ 都不成立
• 传递性，$\forall x,y,z\in A$，若 $xRy,yRz$ 则 $xRz$

则称 $R$ 为定义在 $A$ 上的非严格偏序偏序关系，记作 $\prec$。

容易看出偏序集与有向无环图有着自然的联系，设图 $G=(V,E)$ 满足 $V=A,E=\{(x,y)|x\prec y,x,y\in A\}$，那么 $G$ 为一张有向无环图，其传递闭包就是其本身。

以上两种关系统称为偏序关系。若集合 $A$ 上定义了一个偏序 $R$，则 $A$ 和偏序 $R$ 为偏序集，记作 $(A,R)$。

容易推导得出以下结论：

• 若集合 $A$ 上定义了一个非严格偏序 $\preccurlyeq$，那么可以自然地推导出严格偏序 $\prec$，$a\prec b$ 当且仅当 $a\preccurlyeq b$ 且 $a\neq b$
• 若集合 $A$ 上定义了一个严格偏序 $\prec$，那么可以自然地推导出非严格偏序 $\preccurlyeq$，$a\preccurlyeq b$ 当且仅当 $a\prec b$ 或 $a=b$
• 给定集合 $A$ 上的一个非严格偏序 $\preccurlyeq$，那么其逆关系 $\succcurlyeq$ 也是非严格偏序。
• 给定集合 $A$ 上的一个严格偏序 $\prec$，那么其逆关系 $\succ$ 也是严格偏序。

全序是一种特殊的偏序关系，在偏序关系的定义中只要求部分元素可比，而全序关系要求 $\forall x,y\in A$ 都有 $xRy$ 或 $yRx$，即任意两个元素都可比。

下面举几个例子吧：

• 定义在实数集 $\mathbb{R}$ 上的 $\leq$ 显然是一种偏序关系，这个偏序同时也是全序。
• 定义在 $\mathbb{N}*$ 上的整除（$\mid$）运算也是一种偏序关系，但这个偏序不是全序。
• 定义在复数集 $\mathbb{C}$ 上的 $\leq$ 显然是一种偏序关系，但这个偏序不是全序。
• 对于集合 $S$ 的两个子集 $S_1,S_2\subseteq S$，$S_1\leq S_2\Rightarrow S_1\subseteq S_2$，则 $(T=\{S'|S'\subseteq T\},\leq)$ 是一种偏序关系，但这个偏序不是全序。

Dilworth 定理

终于（快要）进入正题了。

对于偏序集 $(A,R)$，我们做出如下定义：

• 集合 $A'\subseteq A$ 为偏序集的一个链当且仅当 $\forall x,y\in A'$ 都有 $xRy$ 或 $yRx$。
• 集合 $A'\subseteq A$ 为偏序集的一个反链当且仅当 $\forall x,y\in A',xRy$ 和 $yRx$ 都不成立。
• 一个链的集合 $S=\{S_1,S_2,\dots,S_k\}$ 为偏序集的链覆盖，当且仅当 $S_1,S_2,\dots,S_k$ 均为链且 $\forall x\in A,{\exists} i\in[1,k]$ 使得 $x\in S_i$。该链覆盖的大小为 $k$

Dilworth 定理说的是这样一件事：一个偏序集的最大反链大小 = 最小链覆盖。

如果你前面偏序集的定义没搞懂，那么你可以这样理解这个定理：

• 对于满足 $\forall u,v,w\in V,\;(u,v),(v,w)\in E\Rightarrow (u,w)\in E$ 的图 $G=(V,E)$，有 $G$ 的最大独立集等于 $G$ 的最小可相交路径覆盖。

• 即：有向无环图DAG的最大独立集 = 有向无环图DAG最少不相交路径覆盖。

证明

考虑第二数学归纳法，假设当 $|A|\leq m$ 时候命题成立，下证 $|A|=m+1$ 时命题成立。

考虑 $A$ 中的一个极大元 $x$（$\forall y\in A$，若 $x,y$ 可比则都有 $xRy$），设 $A'=A-\{x\}$，由归纳假设 $A'$ 中最大反链大小等于最小链覆盖，假设其大小都为 $k$。

假设 $A'$ 可划分为 $k$ 个链 $\{C_1,C_2,\dots,C_k\}$，$A'$ 中大小为 $k$ 的反链有 $r$ 个，分别为 $S_1,S_2,\dots,S_r$。

那么显然 $S_i$ 是在 $k$ 条链中各取一个元素（否则假设 $\exists x,y\in S_i$ 且 $x,y$ 在同一条链中，那么 $x,y$ 必然可比，矛盾），不妨设 $s_{i,j}$ 为满足 $u\in S_i,u\in C_j$ 的 $u$。再记集合 $B=\{\max(s_{i,1}),\max(s_{i,2}),\cdots,\max(s_{i,k})\}$，即对于每条链，这条链上被包含在这 $r$ 个大小为 $k$ 的反链中的元素中大小最大的那个组成的集合（注意，由于所有这样的点都在同一条链上，故它们两两之间都是可比的，因此也有了 “最大值” 的定义）

那么 $B$ 为一个长度为 $k$ 的反链（否则假设 ${\exists} b_i,b_j\in B$ 满足 $b_iRb_j$，那么根据 $b_j=\max(s_{l,j})$ 就有 $b_iRs_{1,j},b_iRs_{2,j},\dots,b_iRs_{r,j}$，而设 $b_i=s_{t,i}$（$b_i$ 是第 $t$ 个反链在第 $i$ 条链上选出的点），根据反链的定义有 $b_i$ 与 $s_{t,j}$ 不可比，矛盾！

现在考虑加入一个元素 $\{x\}$ 对答案的影响。

1. 若 $\forall y\in B$ 都有 $x,y$ 不可比，那么 $B'=B\cup\{x\}$ 为一条长度为 $k+1$ 的反链，而加入一个元素，最大反链长度和最小链覆盖大小最少变化 $0$，至多变化 $1$，故 $S$ 最大反链大小就是 $k+1$，最小链覆盖大小至少为 $k$，至多为 $k+1$，而假设最小链覆盖大小为 $k$，那么由于反链 $B'$ 大小为 $k+1$，根据抽屉原理知 ${\exists} u,v\in B'$ 满足 $u,v$ 被划分到了同一条链中，矛盾。那么最小链覆盖大小就是 $k+1$。
2. 若 ${\exists} y\in B$ 使得 $x,y$ 可比，那么由 $x$ 为极大元可知 $xRy$，而 $B$ 为反链可知这样的 $y$ 最多只有一个，假设 $y\in C_j$，那么考虑集合 $D=\{s_{1,j},s_{2,j},\dots,s_{r,j},x\}$，再记 $T=S-D$，那么 $T$ 的最大反链大小为 $k-1$（因为 $S$ 中所有大小为 $k$ 的反链都被抠掉了一个元素，而大小为 $k-1$ 的反链显然存在），由归纳假设 $T$ 的最小链覆盖大小也为 $k-1$，而 $D$ 显然为一条链，故 $S$ 的最小链覆盖大小为 $k$，得证。

故 $|A|=m+1$ 时命题成立。

而 $|A|\leq 1$ 命题显然成立。

根据数学归纳法知命题成立！

通俗解释

Dilworth定理，一言以蔽之，偏序集能划分成的最少的全序集个数等于最大反链的元素个数。——————litble

狄尔沃斯定理 (Dilworth’s theorem) 亦称偏序集分解定理，是关于偏序集的极大极小的定理，该定理断言：对于任意有限偏序集，其最大反链中元素的数目必等于最小链划分中链的数目。此定理的对偶形式亦真，它断言：对于任意有限偏序集，其最长链中元素的数目必等于其最小反链划分中反链的数目，由偏序集 P 按如下方式产生的图 G 称为偏序集的可比图：G 的节点集由 P 的元素组成，而 e 为 G 中的边，仅当 e 的两端点在 P 中是可比较的，有限全序集的可比图为完全图——百度百科

偏序集中的概念

链 : D 中的一个子集 C 满足 C 是全序集 及C中所有元素都可以比较大小

反链 : D 中的一个子集 B 满足 B 中任意非空子集都不是全序集 即所有元素之间都不可以比较大小

链覆盖 : 若干个链的并集为 D ，且两两之间交集为 ∅

反链覆盖 : 若干个反链的并集为 D ，且两两之间交集为∅

最长链 : 所有链中元素个数最多的 (可以有多个最长链)

最长反链 : 所有反链中元素个数最多的 (可以有多个最长反链

偏序集高度 : 最长链的元素个数
偏序集宽度 : 最长反链中的元素个数

最小链覆盖（使链最少）= 最长反链长度 = 偏序集宽度
最小反链覆盖 = 最长链长度 = 偏序集深度

Dilworth定理在序列中的应用

洛谷 P1020 导弹拦截

思路：
题目中说以后每一发都不能高于前一发，我们能拦截的导弹高度是非递增序列，第一问显然就是最大非递增序列的长度，因为这里范围比较大，所以我们单调队列 + 二分优化 DP。
第二问要最少配备多少套拦截系统，就是问这个序列最少可以划分为多少个非递增序列，根据 Dilworth 定理，我们只需求最长上升子序列的长度就是答案。

int a[N];
int d[N];
int main(){
    int tot = 0;
    while(scanf("%d",&a[++tot]) == 1){}
    tot --;
    int len = 1;
    d[1] = a[1];
    rep(i,2,tot){
        if(a[i] <= d[len]) d[++len] = a[i];
        else {
            int pos = upper_bound(d +1,d + len + 1,a[i],greater<int>()) - d;
            d[pos] = a[i];
        }
    }
    cout << len<<endl;
    d[1] = a[1];
    len = 1;
    rep(i,2,tot){
        if(a[i] > d[len]) d[++len] = a[i];
        else {
            int pos = lower_bound(d+1,d +len + 1,a[i]) - d;
            d[pos] = a[i];
        }
    }
    cout << len;
}

Codeforce 1296 E

给你一个字符串，然后你可以数字给每个位置的字符染色，只有相邻的颜色不同的字符才可以交换位置。问你是否最小用多少颜色使得这个字符串经过数次交换后呈字典序从小到大分布。然后输出染色的结果。
思路：
题目就是问你最少用多少个最长不下降子序列凑成这个序列。根据 Dilworth 定理可得，是最大反链的个数，即最长下降子序列的长度。然后构造每个字符的颜色就是当前以它为结尾的字符串中最长下降子序列的长度。

int r[26];
int vis[N];
int main(){
    memset(vis,0,sizeof vis);
    int n;
    cin >> n;
    string s;
    cin >> s;
    int M = -INF;
    for(int i = 0;i < n;++i){
        int d = 0;
        for(int j = s[i] - 'a' + 1;j < 26;++j){
            d = max(d,r[j]);
        }
        r[s[i]-'a'] = d + 1;
        vis[i] = d + 1;
        M = max(M,d + 1);
    }
    cout << M<<endl;
    for(int i = 0;i < n;++i) cout << vis[i] <<' ';
}

牛客挑战赛 36 C - 纸飞机

思路：
题意显然问去除一个数后剩余的序列最少可以被多少个严格递减序列组成。
根据 Dilworth 定理，我们求反链的最大长度，即不严格递减序列的最大长度。
如果我们每删去一个数求一次肯定会超时，这样想，我们求出原来序列的最长不递减序列，每删去一个数，是否会影响原来序列的最长不递减序列的长度？

如果这个数不在原来的最长不递减序列中或者这个数所在的位置不唯一（1 3 2 4）, 则并不会影响原来的结果，而如果这个数在里面且唯一，则答案会减一。

那如果判断呢？
由于范围比较大， n 2 n^2 n2 肯定超时，所以我们用树状数组优化， d p [i] dp[i] dp[i] 代表着以 i i i 结尾的最大长度，假设所谓最大长度为 a n s ans ans。求完后，我们倒序判断一个数是否在所求的最长不递减序列中。我们增加辅助数组 a x ax ax， a x [i] ax[i] ax[i] 代表最长序列中第 i i i 个位置的数的最大值， v i s [i] vis[i] vis[i] 表示第 i i i 个数是否在最长序列中。
首先 d p [i] = a n s dp[i]=ans dp[i]=ans 的数肯定在最长序列中，然后对于第 i i i 个数字，如果 a [i] < = a x [ d p [ i ] + 1 ] a[i]<=ax[dp[i]+1] a[i]<=ax[dp[i]+1]，那么说明第 i i i 个数在最长序列中，我们更新最大的 a x [ d p [i] ] ax[dp[i]] ax[dp[i]] 值，并开一 n u m num num 数组统计最长序列中每个位置的数有几个。

最后判断输出即可。

int n;
int dp[N];
int c[N],ax[N];
int a[N],b[N];
bool vis[N];int num[N];
void modify(int x,int y){
    for(;x <= n;x += x&(-x)){
        c[x] = max(c[x],y);
    }
}
int getMax(int x){
    int ans = 0;
    for(;x;x -= x&(-x)){
        ans = max(ans,c[x]);
    }
    return ans;
}
int main(){
    n = read();
    rep(i,1,n) a[i] = b[i] = read();
    sort(b + 1,b + n + 1);
    int m = unique(b + 1,b + n + 1) - b - 1;
    rep(i,1,n) a[i] = lower_bound(b+1,b+m+1,a[i]) - b;
    int ans = 0;
    rep(i,1,n){
        dp[i] = getMax(a[i]) + 1;
        modify(a[i],dp[i]);
        ans = max(ans,dp[i]);
    }
    cout <<ans << endl;
    ax[ans+1] = INF;
    fori(i,n,1){
        if(a[i] <= ax[dp[i]+1]){
            vis[i] = 1;
            num[dp[i]] ++;
            ax[dp[i]] = max(ax[dp[i]],a[i]);
        }
    }
    rep(i,1,n){
        if(num[dp[i]] == 1&&vis[i]) cout<<ans-1<<' ';
        else cout<<ans<<' ';
    }
}

Dilworth定理在DAG中的应用

DAG 中，有如下的一些定义和性质：

链：一条链是一些点的集合，链上任意两个点x, y，满足要么 x 能到达 y ，要么 y 能到达 x 。

反链：一条反链是一些点的集合，链上任意两个点x, y，满足 x 不能到达 y，且 y 也不能到达 x。

一个定理：最长反链长度 = 最小链覆盖（用最少的链覆盖所有顶点）

对偶定理：最长链长度 = 最小反链覆盖

那么我们要求出的就是这个有向无环图的最小链覆盖了。
最小链覆盖即路径可以相交的最小路径覆盖。 ————by Eirlys_North

DAG的最小路径覆盖

定义：在一个有向图中，找出最少的路径，使得这些路径经过了所有的点。

最小路径覆盖分为最小不相交路径覆盖和最小可相交路径覆盖。

• 最小不相交路径覆盖：每一条路径经过的顶点各不相同。

  • 如图，其最小路径覆盖数为 3。即$1 \rightarrow 3 \rightarrow 4,\;2,\;5$
  • 定理：有向无环图DAG的最小路径点覆盖包含的路径条数，等于 $n$ 减去拆点二分图G2的最大匹配数。

• 最小可相交路径覆盖：每一条路径经过的顶点可以相同。

  • 如果其最小路径覆盖数为 2。即$1 \rightarrow 3 \rightarrow 4,\;2 \rightarrow 3 \rightarrow 5$
  • 定理：先用$floyd$求出原图的传递闭包，如果 $a$ 到 $b$ 有路， 那么就加边 $a\rightarrow b$ ，即把图中所有间接连通的点在原图中给他连一条边让它直接连通，然后就转化成了最少不相交路径覆盖问题
    • 所以我们先对有向图传递闭包（偏序关系补全），然后$n^2$建立二分图，最后求最大匹配即可。

特别的，每个点自己也可以称为是路径覆盖，只不过路径的长度是 0。 ——justPassBy

---

bzoj1143 祭祀

思路：

题目很显然让我们求一个最大的集合，集合中的点两两之间不能相互到达，这显然就是让求最大反链的长度，最长反链的长度 = 最小链覆盖。
即 DAG 最小可相交路径覆盖，先传递闭包，然后拆点二分图最大匹配即可。

int w[220][220];
int head[220],tot;
bool vis[205];
int match[205];
struct Edge{
    int next;
    int to;
}edge[N];
inline void add(int from,int to){
    edge[++tot].next = head[from];
    edge[tot].to = to;
    head[from] = tot;
}
void floyd(int n){
    rep(k,1,n){
        rep(i,1,n){
            rep(j,1,n){
                w[i][j] |= w[i][k]&w[k][j];
            }
        }
    }
}
bool dfs(int x){
    for(int i = head[x];i;i = edge[i].next){
        int y = edge[i].to;
        if(!vis[y]){
            vis[y] = 1;
            if(!match[y]||dfs(match[y])){
                match[y] = x;return true;
            }
        }
    }
    return false;
}
int main(){
    int n = read(),m = read();
    rep(i,1,m){
        int u = read(),v = read();
        w[u][v] = 1;
    }
    floyd(n);//传递闭包
    rep(i,1,n){
        rep(j,1,n){
            if(w[i][j]) add(i,j+n);
        }
    }
    int ans = 0;
    rep(i,1,n){//二分图最大匹配
        memset(vis,0,sizeof vis);
        if(dfs(i)) ans ++;
    }
    cout <<n - ans<<endl;
}

本文查阅诸多网上博客资料所写，如有冒犯请留言。