参考《算法竞赛进阶指南》、AcWing题库

线段树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
class SegTree {
public: 
    struct Node {
        int l = 0, r = 0;
        int sum = 0;
    };

    vector<Node> tr;
    vector<int> a;
    int n;

    SegTree() {}

    SegTree(vector<int> &a) {
        n = a.size();
        this->a = a;
        tr.resize(n * 4 + 1);
        build(1, 1, n);
    }

    void pushup(Node &u, Node &ls, Node &rs) {
        u.sum = ls.sum + rs.sum;
    }

    void pushup(int u) {
        pushup(tr[u], tr[u << 1], tr[u << 1 | 1]);
    }

    void build(int u, int l, int r) {
        tr[u] = {l, r};
        if (l == r) {
            tr[u].sum = a[l - 1];
            return;
        }

        int mid = l + r >> 1;
        build(u << 1, l, mid);
        build(u << 1 | 1, mid + 1, r);
        pushup(u);
    }

    void modify(int u, int x, int v) {
        if (tr[u].l == tr[u].r) {
            tr[u].sum = v;
            return;
        }
        int mid = tr[u].l + tr[u].r >> 1;
        if (x <= mid) modify(u << 1, x, v);
        else modify(u << 1 | 1, x, v);
        pushup(u);
    }

    Node ask(int u, int l, int r) {
        if (l <= tr[u].l && tr[u].r <= r) return tr[u];

        int mid = tr[u].l + tr[u].r >> 1;
        if (r <= mid) return ask(u << 1, l, r);
        if (l > mid) return ask(u << 1 | 1, l, r);
        
        Node ans;
        auto left = ask(u << 1, l, r);
        auto right = ask(u << 1 | 1, l, r);
        pushup(ans, left, right);
        return ans;
    }
};

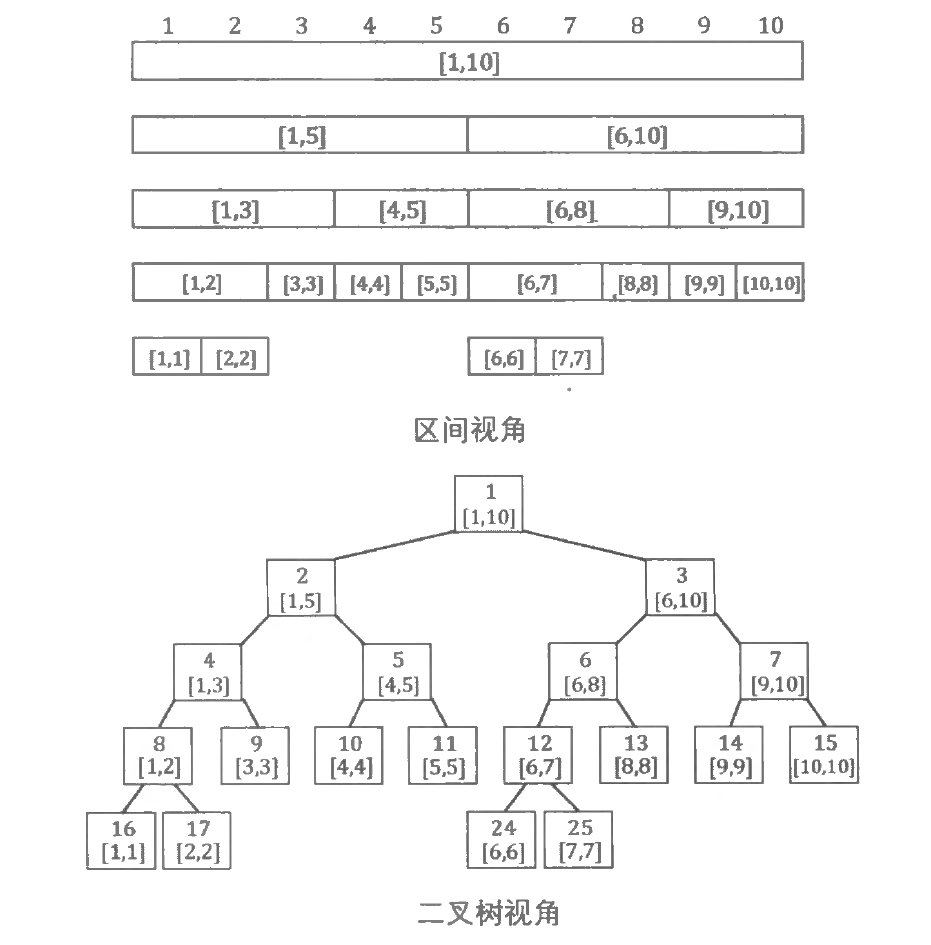
线段树 (Segment Tree) 是一种基于分治思想的二叉树结构, 用于在区间上进行信息统计。与按照二进制位 (2 的次幂) 进行区间划分的树状数组相比, 线段树是一种更加通用的结构:

  1. 线段树的每个节点都代表一个区间。
  2. 线段树具有唯一的根节点, 代表的区间是整个统计范围, 如 [1,N][1, N] 。
  3. 线段树的每个叶节点都代表一个长度为 1 的元区间 [x,x][x, x] 。
  4. 对于每个内部节点 [l,r][l, r], 它的左子节点是 [l,mid][l, m i d], 右子节点是 [mid+1,r][m i d+1, r], 其中 mid=(l+r)/2mid=(l+r) / 2 (向下取整)。

上图展示了一棵线段树。可以发现, 除去树的最后一层, 整棵线段树一定是一棵完
全二叉树, 树的深度为 O(log⁡N)\mathrm{O}(\log N) 。因此, 我们可以按照与二叉堆类似的 “父子 2 倍” 节点编号方法:

  1. 根节点编号为 1 。
  2. 编号为 xx 的节点的左子节点编号为 x∗2 或 x<<1x * 2 \text{ 或 } x << 1, 右子节点编号为 x∗2+1 或 x<<1  ∣  1x * 2+1 \text{ 或 } x << 1 \;| \;1 。

这样一来, 我们就能简单地使用一个 struct 数组来保存线段树。当然, 树的最后一层节点在数组中保存的位置不是连续的, 直接空出数组中多余的位置即可。在理想情况下, NN 个叶节点的满二叉树有 N+N/2+N/4+⋯+2+1=2N−1N+N / 2+N / 4+\cdots+2+1=2 N-1 个节点。因为在上述存储方式下, 最后还有一层产生了空余, 所以保存线段树的数组长度要不小于 4N4 N 才能保证不会越界。

线段树的建树、pushup操作

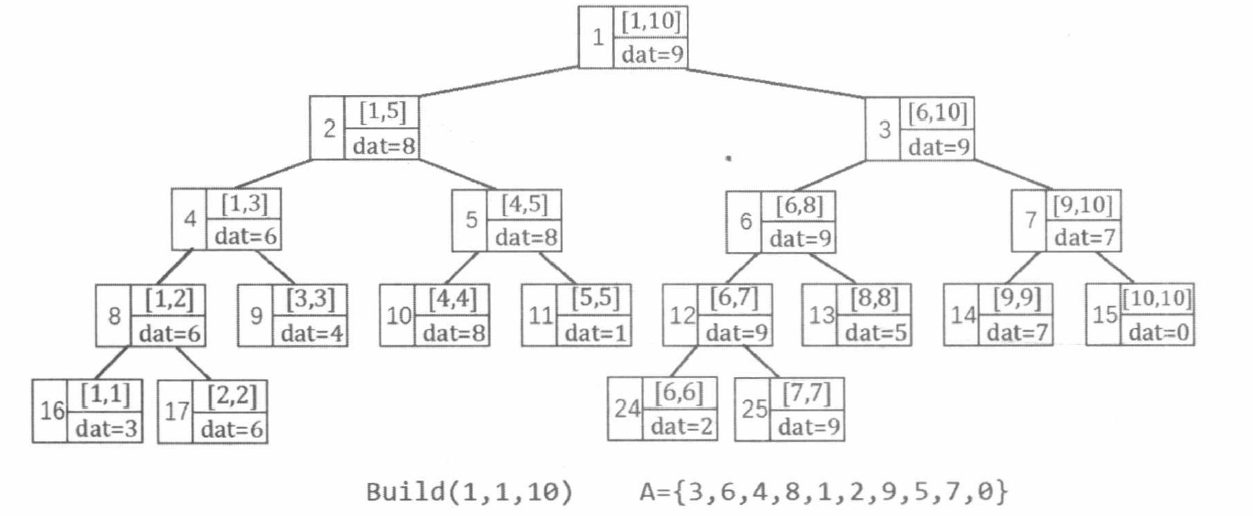
线段树的基本用途是对序列进行维护, 支持查询与修改指令。给定一个长度为 NN 的序列 AA, 我们可以在区间 [1,N][1, N] 上建立一棵线段树, 每个叶节点 [i,i][i, i] 保存 A[i]A[i] 的值。线段树的二叉树结构可以很方便地从下往上传递信息。以区间最大值问题为例, 记 dat⁡(l,r)\operatorname{dat}(l, r) 等于 max⁡l≤i≤r{A[i]}\max _{l \leq i \leq r}\{A[i]\}, 显然 dat⁡(l,r)=max⁡(dat⁡(l,mid⁡),dat⁡(mid⁡+1,r))\operatorname{dat}(l, \mathrm{r})=\max (\operatorname{dat}(l, \operatorname{mid}), \operatorname{dat}(\operatorname{mid}+1, r)) 。

下面这段代码建立了一棵线段树并在每个节点上保存了对应区间的最大值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
struct Node {
	int l, r;
	int dat;
} tr[SIZE * 4]; // struct数组存储线段树


void pushup(Node &u, Node &l, Node &r) {
	u.dat = max(l.dat, r.dat);
}

void pushup(int u) {
	pushup(tr[u], tr[u << 1], tr[u << 1 | 1]);
}

void build(int u, int l, int r) {
	tr[u] = {l, r}; // 节点p代表区间[l,r]
	if (l == r) { // 叶节点
		tr[u].dat = a[l]; 
		return; 
	} 

	int mid = l + r >> 1; // 折半
	build(u << 1, l, mid); // 左子节点[l,mid]，编号u*2
	build(u << 1 | 1, mid + 1, r); // 右子节点[mid+1,r]，编号u*2+1
	pushup(u); // 从下往上传递信息
}

build(1, 1, n); // 调用入口

线段树的单点修改

单点修改是一条形如 “ C  x  v\mathrm{C} \;x \;v ” 的指令, 表示把 A[x]A[x] 的值修改为 vv 。

在线段树中, 根节点 (编号为 1 的节点) 是执行各种指令的入口。我们需要从根节 点出发, 递归找到代表区间 [x,x][x, x] 的叶节点, 然后从下往上更新 [x,x][x, x] 以及它的所有祖先节点上保存的信息, 如下图所示。时间复杂度为 O(log⁡N)O(\log N) 。

1
2
3
4
5
6
7
8
9
10
11
12
13
void modify(int u, int x, int v) {
	if (tr[u].l == tr[u].r) { // 找到叶节点
		tr[u].dat = v; 
		return; 
	} 

	int mid = tr[u].l + tr[u].r >> 1;
	if (x <= mid) modify(u << 1, x, v); // x属于左半区间
	else modify(u << 1 | 1, x, v); // x属于右半区间
	pushup(u); // 从下往上更新信息
}

change(1, x, v); // 调用入口

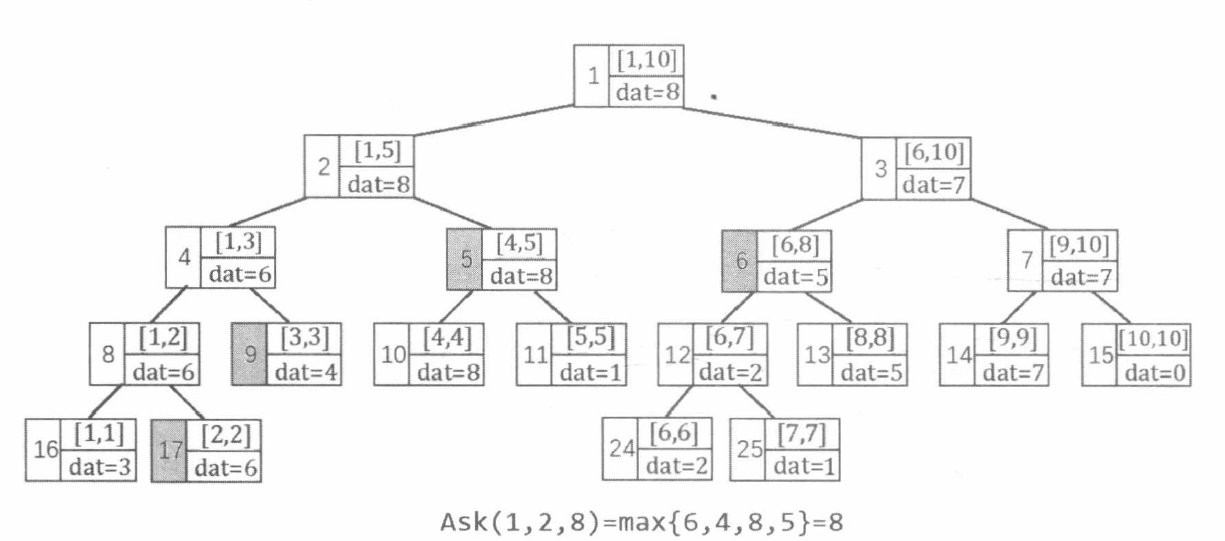
线段树的区间查询

区间查询是一条形如 “ Q  l  r\mathrm{Q} \;l \;r ” 的指令, 例如查询序列 AA 在区间 [l,r][l, r] 上的最大值, 即 max⁡l≤i≤r{A[i]}\max _{l \leq i \leq r}\{A[i]\} 。我们只需要从根节点开始, 递归执行以下过程:

  1. 若 [l,r][l, r] 完全覆盖了当前节点代表的区间, 则立即回溯, 并且该节点的 datd a t 值为候选答案。
  2. 若左子节点与 [l,r][l, r] 有重叠部分, 则递归访问左子节点。
  3. 若右子节点与 [l,r][l, r] 有重叠部分, 则递归访问右子节点。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Node ask(int u, int l, int r) {
	if (l <= tr[u].l && r >= tr[u].r) return tr[u];

	int mid = tr[u].l + tr[u].r >> 1;
	if (r <= mid) return ask(u << 1, l, r); // 只与左子节点有重叠
	if (l > mid) return ask(u << 1 | 1, l, r); // 只与右子节点有重叠

	// 与左右子节点均有重叠
	auto left = ask(u << 1, l, r);
	auto right = ask(u << 1 | 1, l, r);
	Node ans;
	pushup(ans, left, right);
	return ans;
}
1
2
3
4
5
6
7
8
9
10
11
int ask(int u, int l, int r) {
	if (l <= tr[u].l && r >= tr[u].r) return tr[u].dat; // 完全包含，直接返回

	int mid = tr[u].l + tr[u].r >> 1;
	int val = 0;
	if (l <= mid) val = max(val, ask(u << 1, l, r)); // 左子节点有重叠
	if (r > mid) val = max(val, ask(u << 1 | 1, l, r)); // 右子节点有重叠
	return val;
}

ask(1, l, r); // 调用入口

该查询过程会把询问区间 [l,r][l, r] 在线段树上分成 O(log⁡N)O(\log N) 个节点, 取它们的最大值作为答案。为什么是 O(log⁡N)O(\log N) 个呢? 仔细分析上述过程, 在每个节点 [pl,pr]\left[p_{l}, p_{r}\right] 上, 设 mid⁡=(pl+pr)/2\operatorname{mid}=\left(p_{l}+p_{r}\right) / 2 (向下取整), 可能会出现以下几种情况:

  1. l≤pl≤pr≤rl \leq p_{l} \leq p_{r} \leq r, 即完全覆盖了当前节点, 直接返回。
  2. pl≤l≤pr≤rp_{l} \leq l \leq p_{r} \leq r, 即只有 ll 处于节点之内。
    (1) l>midl>\mathrm{mid}, 只会递归右子树。
    (2) l≤midl \leq m i d, 虽然递归两棵子树, 但是右子节点会在递归后直接返回。
  3. l≤pl≤r≤prl \leq p_{l} \leq r \leq p_{r}, 即只有 rr 处于节点之内, 与情况 2 类似。
  4. pl≤l≤r≤prp_{l} \leq l \leq r \leq p_{r}, 即 ll 与 rr 都位于节点之内。
    (1) l,rl, r 都位于 midm i d 的一侧, 只会递归一棵子树。
    (2) l,rl, r 分别位于 midm i d 的两侧, 递归左右两棵子树。

也就是说, 只有情况 4(2) 会真正产生对左右两棵子树的递归。请读者思考, 这种 情况至多发生一次, 之后在子节点上就会变成情况 2 或 3 。因此, 上述查询过程的时间复杂度为 O(2log⁡N)=O(log⁡N)O(2 \log N)=O(\log N) 。从宏观上理解, 相当于 l,rl, r 两个端点分别在线段树上划分出一条递归访问路径, 情况 4(2) 在两条路径于从下往上的第一次交会处产生。

至此, 线段树已经能够像 倍增 节的 ST 算法一样处理区间最值问题, 并且还支持 动态修改某个数的值。同时, 线段树也已经能支持上一节中树状数组的单点增加与查询前缀和指令。在讨论区间修改之前, 我们先来通过几道例题加深对线段树的印象。

例题

1275. 最大数

给定一个正整数数列 a1,a2,…,ana_1,a_2,…,a_n，每一个数都在 0∼p−10 \sim p-1 之间。

可以对这列数进行两种操作：

  1. 添加操作：向序列后添加一个数，序列长度变成 n+1n+1；
  2. 询问操作：询问这个序列中最后 LL 个数中最大的数是多少。

程序运行的最开始，整数序列为空。

一共要对整数序列进行 mm 次操作。

写一个程序，读入操作的序列，并输出询问操作的答案。

输入格式

第一行有两个正整数 m,pm,p，意义如题目描述；

接下来 mm 行，每一行表示一个操作。

如果该行的内容是 Q L，则表示这个操作是询问序列中最后 LL 个数的最大数是多少；

如果是 A t，则表示向序列后面加一个数，加入的数是 (t+a) mod p(t+a)\ mod\ p。其中，tt 是输入的参数，aa 是在这个添加操作之前最后一个询问操作的答案（如果之前没有询问操作，则 a=0a=0）。

第一个操作一定是添加操作。对于询问操作，L>0L>0 且不超过当前序列的长度。

输出格式

对于每一个询问操作，输出一行。该行只有一个数，即序列中最后 LL 个数的最大数。

数据范围

1≤m≤2×1051 \le m \le 2 \times 10^5,
1≤p≤2×1091 \le p \le 2 \times 10^9,
0≤t<p0 \le t < p

输入样例：

1
2
3
4
5
6
7
8
9
10
11
10 100
A 97
Q 1
Q 1
A 17
Q 2
A 63
Q 1
Q 1
Q 3
A 99

输出样例：

1
2
3
4
5
6
97
97
97
60
60
97

样例解释

最后的序列是 97,14,60,9697,14,60,96。

算法分析

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
#include <iostream>
using namespace std;

using LL = long long;

const int N = 2e5 + 10;

int m, p;

struct Node {
    int l, r;
    int dat;
} tr[N * 4];

void pushup(int u) {
    tr[u].dat = max(tr[u << 1].dat, tr[u << 1 | 1].dat);
}
void build(int u, int l, int r) {
    tr[u] = {l, r};
    if (l == r) return;
    
    int mid = l + r >> 1;
    build(u << 1, l, mid);
    build(u << 1 | 1, mid + 1, r);
}

int ask(int u, int l, int r) {
    if (l <= tr[u].l && r >= tr[u].r) return tr[u].dat;
    
    int mid = tr[u].l + tr[u].r >> 1;
    int val = 0;
    if (l <= mid) val = ask(u << 1, l, r);
    if (r > mid) val = max(val, ask(u << 1 | 1, l, r));
    
    return val;
}

void modify(int u, int x, int v) {
    if (tr[u].l == tr[u].r) {
        tr[u].dat = v;
    } else {
        int mid = tr[u].l + tr[u].r >> 1;
        if (x <= mid) modify(u << 1, x, v);
        else modify(u << 1 | 1, x, v);
        pushup(u);
    }
}


int main() {
    int n = 0, last = 0;
    cin >> m >> p;
    
    build(1, 1, m);
    
    int x;
    char op;
    while (m--) {
        cin >> op >> x;
        if (op == 'Q') {
            last = ask(1, n - x + 1, n);
            cout << last << endl;
        } else {
            modify(1, ++n, ((LL)last + x) % p);
        }
    }
}

245. 你能回答这些问题吗

给定长度为 NN 的数列 AA，以及 MM 条指令，每条指令可能是以下两种之一：

  1. 1 x y，查询区间 [x,y][x,y] 中的最大连续子段和，即 max⁡x≤l≤r≤y\max_{x \le l \le r \le y}{∑i=lrA[i]\sum\limits^r_{i=l} A[i]}。
  2. 2 x y，把 A[x]A[x] 改成 yy。

对于每个查询指令，输出一个整数表示答案。

输入格式

第一行两个整数 N,MN,M。

第二行 NN 个整数 A[i]A[i]。

接下来 MM 行每行 33 个整数 k,x,yk,x,y，k=1k=1 表示查询（此时如果 x>yx>y，请交换 x,yx,y），k=2k=2 表示修改。

输出格式

对于每个查询指令输出一个整数表示答案。

每个答案占一行。

数据范围

N≤500000,M≤100000N \le 500000, M \le 100000,
−1000≤A[i]≤1000-1000 \le A[i] \le 1000

输入样例：

1
2
3
4
5
5 3
1 2 -3 4 5
1 2 3
2 2 -1
1 3 2

输出样例：

1
2
2
-1

算法分析

在线段树上的每个节点上, 除了区间端点外, 再维护 4 个信息: 区间和 sum, 区 间最大连续子段和 dat, 紧靠左端的最大连续子段和 1max1 \mathrm{max}, 紧靠右端的最大连续子段 和 rmax。
线段树的整体框架不变, 我们只需完善在 build 和 change 函数中从下往上传递的 信息:

1
2
3
4
t[p].sum = t[2 * p].sum + t[2 * p + 1].sum;
t[p].lmax = max(t[2 * p].lmax, t[2 * p].sum + t[2 * p + 1].lmax);
t[p].rmax = max(t[2 * p + 1].rmax, t[2 * p + 1].sum + t[2 * p].rmax);
t[p].dat = max({t[2 * p].dat, t[2 * p + 1].dat, t[2 * p].rmax + t[2 * p + 1].lmax});

从这道题目我们也可以看出, 线段树作为一种比较通用的数据结构, 能够维护各式各样的信息, 前提是这些信息容易按照区间进行划分与合并 (又称满足区间可加性)。 我们只需要在父子传递信息和更新答案时稍作变化即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
//Author:XuHt
#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 500006, INF = 0x3f3f3f3f;
int n, m, a[N];
struct T {
	int l, r, s, lx, rx, ans;
} t[N*4];

void build(int p, int l, int r) {
	t[p].l = l;
	t[p].r = r;
	if (l == r) {
		t[p].s = t[p].lx = t[p].rx = t[p].ans = a[l];
		return;
	}
	int mid = (l + r) >> 1;
	build(p << 1, l, mid);
	build(p << 1 | 1, mid + 1, r);
	t[p].s = t[p<<1].s + t[p<<1|1].s;
	t[p].lx = max(t[p<<1].lx, t[p<<1].s + t[p<<1|1].lx);
	t[p].rx = max(t[p<<1|1].rx, t[p<<1].rx + t[p<<1|1].s);
	t[p].ans = max(max(t[p<<1].ans, t[p<<1|1].ans), t[p<<1].rx + t[p<<1|1].lx);
}

void change(int p, int x, int y) {
	if (t[p].l == t[p].r) {
		t[p].s = t[p].lx = t[p].rx = t[p].ans = y;
		return;
	}
	int mid = (t[p].l + t[p].r) >> 1;
	if (x <= mid) change(p << 1, x, y);
	else change(p << 1 | 1, x, y);
	t[p].s = t[p<<1].s + t[p<<1|1].s;
	t[p].lx = max(t[p<<1].lx, t[p<<1].s + t[p<<1|1].lx);
	t[p].rx = max(t[p<<1|1].rx, t[p<<1].rx + t[p<<1|1].s);
	t[p].ans = max(max(t[p<<1].ans, t[p<<1|1].ans), t[p<<1].rx + t[p<<1|1].lx);
}

T ask(int p, int l, int r) {
	if (l <= t[p].l && r >= t[p].r) return t[p];
	T a, b, ans;
	a.s = a.lx = a.rx = a.ans = b.s = b.lx = b.rx = b.ans = -INF;
	ans.s = 0;
	int mid = (t[p].l + t[p].r) >> 1;
	if (l <= mid) {
		a = ask(p << 1, l, r);
		ans.s += a.s;
	}
	if (r > mid) {
		b = ask(p << 1 | 1, l, r);
		ans.s += b.s;
	}
	ans.ans = max(max(a.ans, b.ans), a.rx + b.lx);
	ans.lx = max(a.lx, a.s + b.lx);
	ans.rx = max(b.rx, b.s + a.rx);
	if (l > mid) ans.lx = max(ans.lx, b.lx);
	if (r <= mid) ans.rx = max(ans.rx, a.rx);
	return ans;
}

int main() {
	cin >> n >> m;
	for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
	build(1, 1, n);
	while (m--) {
		int t, x, y;
		scanf("%d %d %d", &t, &x, &y);
		if (t == 1) {
			if (x > y) swap(x, y);
			cout << ask(1, x, y).ans << endl;
		}
		else change(1, x, y);
	}
	return 0;
}

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
#include <iostream>
#include <algorithm>
using namespace std;

const int N = 5e5 + 10;

int n, m;
int a[N];
struct Node {
    int l, r;
    int tsum;
    int lmax, rmax;
    int sum;
} tr[4 * N];

void pushup(Node &u, Node &l, Node &r) {
    u.sum = l.sum + r.sum;
    u.lmax = max(l.lmax, l.sum + r.lmax);
    u.rmax = max(r.rmax, r.sum + l.rmax);
    u.tsum = max({l.tsum, r.tsum, l.rmax + r.lmax});
}

void pushup(int u) {
    pushup(tr[u], tr[u << 1], tr[u << 1 | 1]);
}

void build(int u, int l, int r) {
    tr[u] = {l, r};
    if (l == r) {
        tr[u] = {l, r, a[l], a[l], a[l], a[l]};
        return;
    }
    
    int mid = l + r >> 1;
    build(u << 1, l, mid);
    build(u << 1 | 1, mid + 1, r);
    pushup(u);
}

void modify(int u, int x, int v) {
    if (tr[u].l == tr[u].r) {
        tr[u] = {x, x, v, v, v, v};
        return;
    }
    
    int mid = tr[u].l + tr[u].r >> 1;
    if (x <= mid) modify(u << 1, x, v);
    else modify(u << 1 | 1, x, v);
    pushup(u);
}

Node ask(int u, int l, int r) {
    if (l <= tr[u].l && r >= tr[u].r) return tr[u];
    
    int mid = tr[u].l + tr[u].r >> 1;
    if (r <= mid) return ask(u << 1, l, r);
    if (l > mid) return ask(u << 1 | 1, l, r);
    
    auto left = ask(u << 1, l, r);
    auto right = ask(u << 1 | 1, l, r);
    Node ans;
    pushup(ans, left, right);
    return ans;
}

int main() {
    cin.tie(0);
    ios::sync_with_stdio(false);
    cin >> n >> m;  
    for (int i = 1; i <= n; ++i) cin >> a[i];
    build(1, 1, n);
    
    int k, x, y;
    while (m--) {
        cin >> k >> x >> y;
        if (k == 1) {
            if (x > y) swap(x, y);
            cout << ask(1, x, y).tsum << endl;
        } else {
            modify(1, x, y);   
        }
    }
}

246. 区间最大公约数

给定一个长度为 NN 的数列 AA，以及 MM 条指令，每条指令可能是以下两种之一：

  1. C l r d，表示把 A[l],A[l+1],…,A[r]A[l],A[l+1],…,A[r] 都加上 dd。
  2. Q l r，表示询问 A[l],A[l+1],…,A[r]A[l],A[l+1],…,A[r] 的最大公约数(GCDGCD)。

对于每个询问，输出一个整数表示答案。

输入格式

第一行两个整数 N,MN,M。

第二行 NN 个整数 A[i]A[i]。

接下来 MM 行表示 MM 条指令，每条指令的格式如题目描述所示。

输出格式

对于每个询问，输出一个整数表示答案。

每个答案占一行。

数据范围

N≤500000,M≤100000N \le 500000, M \le 100000,
1≤A[i]≤10181 \le A[i] \le 10^{18},
∣d∣≤1018|d| \le 10^{18}

输入样例：

1
2
3
4
5
6
7
5 5
1 3 5 7 9
Q 1 5
C 1 5 1
Q 1 5
C 3 3 6
Q 2 4

输出样例：

1
2
3
1
2
4

算法分析

根据 “《九章算术》之更相减损术” , 我们知道 gcd⁡(x,y)=gcd⁡(x,y−x)\operatorname{gcd}(x, y)=\operatorname{gcd}(x, y-x) 。它可以进一步扩展到三个数的情况: gcd⁡(x,y,z)=gcd⁡(x,y−x,z−y)\operatorname{gcd}(x, y, z)=\operatorname{gcd}(x, y-x, z-y) 。实际上, 读者用数学归纳法容易证明, 该性质对任意多个整数都成立。

因此, 我们可以构造一个长度为 NN 的新数列 BB, 其中 B[i]=A[i]−A[i−1],B[1]B[i]=A[i]-A[i-1], B[1] 可为任意值。数列 BB 称为 AA 的差分序列。用线段树维护序列 BB 的区间最大公约数。

这样一来, 询问 “ Q  l  r\mathrm{Q} \;l \;r ”, 就等于求出 gcd⁡(A[l],ask⁡(1,l+1,r))\operatorname{gcd}(A[l], \operatorname{ask}(1, l+1, r)) 。

在指令 “ C  l  r  d\mathrm{C} \;l \;r \;d ” 下, 只有 B[l]B[l] 加了 d,B[r+1]d, B[r+1] 被减掉了 dd, 所以在维护 BB 的线段树上只需两次单点修改即可。另外, 询问时需要数列 AA 中的值, 可额外用一个支持 “区间增加、单点查询” 的树状数组对 AA 进行维护。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
//Author:XuHt
#include <cmath>
#include <cstring>
#include <iostream>
#define ll long long
using namespace std;
const int N = 500006;
int n, m;
ll a[N], b[N], c[N];
struct T {
	int l, r;
	ll ans;
} t[N*4];

ll gcd(ll x, ll y) {
	return y ? gcd(y, x % y) : x;
}

void build(int p, int l, int r) {
	t[p].l = l;
	t[p].r = r;
	if (l == r) {
		t[p].ans = b[l];
		return;
	}
	int mid = (l + r) >> 1;
	build(p << 1, l, mid);
	build(p << 1 | 1, mid + 1, r);
	t[p].ans = gcd(t[p<<1].ans, t[p<<1|1].ans);
}

void change_add(int p, int x, ll v) {
	if (t[p].l == t[p].r) {
		t[p].ans += v;
		return;
	}
	int mid = (t[p].l + t[p].r) >> 1;
	if (x <= mid) change_add(p << 1, x, v);
	else change_add(p << 1 | 1, x, v);
	t[p].ans = gcd(t[p<<1].ans, t[p<<1|1].ans);
}

ll ask_t(int p, int l, int r) {
	if (l <= t[p].l && r >= t[p].r) return t[p].ans;
	int mid = (t[p].l + t[p].r) >> 1;
	ll ans = 0;
	if (l <= mid) ans = gcd(ans, ask_t(p << 1, l, r));
	if (r > mid) ans = gcd(ans, ask_t(p << 1 | 1, l, r));
	return abs(ans);
}

void add(int x, ll y) {
	while (x <= n) {
		c[x] += y;
		x += x & -x;
	}
}

ll ask_c(int x) {
	ll ans = 0;
	while (x) {
		ans += c[x];
		x -= x & -x;
	}
	return ans;
}

int main() {
	cin >> n >> m;
	b[0] = 0;
	memset(c, 0, sizeof(c));
	for (int i = 1; i <= n; i++) {
		cin >> a[i];
		b[i] = a[i] - a[i-1];
	}
	build(1, 1, n);
	while (m--) {
		char ch;
		cin >> ch;
		int l, r;
		cin >> l >> r;
		if (ch == 'C') {
			ll d;
			cin >> d;
			change_add(1, l, d);
			add(l, d);
			if (r + 1 <= n) {
				change_add(1, r + 1, -d);
				add(r + 1, -d);
			}
		} else cout << gcd(a[l] + ask_c(l), ask_t(1, l + 1, r)) << endl;
	}
	return 0;
}

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
#include <iostream>
using namespace std;
using LL = long long;

const int N = 500010;

int n, m;
LL a[N];

struct Node {
    int l, r;
    LL val;
    LL sum, d;
} tr[4 * N];

LL gcd(LL a, LL b) {
    return b ? gcd(b, a % b) : a;
}

void pushup(Node &u, Node &l, Node &r) {
    u.sum = l.sum + r.sum;
    u.d = gcd(l.d, r.d);
}

void pushup(int u) {
    pushup(tr[u], tr[u << 1], tr[u << 1 | 1]);
}

void build(int u, int l, int r) {
    tr[u] = {l, r};
    if (l == r) {
        LL b = a[r] - a[r - 1];
        tr[u] = {l, r, b, b, b};
        return;
    }
    
    int mid = l + r >> 1;
    build(u << 1, l, mid);
    build(u << 1 | 1, mid + 1, r);
    pushup(u);
}

void modify(int u, int x, LL v) {
    if (tr[u].l == tr[u].r) {
		LL t = tr[u].val + v;
		tr[u] = {x, x, t, t, t};
        return;
    }
    
    int mid = tr[u].l + tr[u].r >> 1;
    if (x <= mid) modify(u << 1, x, v);
    else modify(u << 1 | 1, x, v);
    pushup(u);
}

Node ask(int u, int l, int r) {
    if (l <= tr[u].l && r >= tr[u].r) return tr[u];
    
    int mid = tr[u].l + tr[u].r >> 1;
    if (r <= mid) return ask(u << 1, l, r);
    if (l > mid) return ask(u << 1 | 1, l, r);
    
    auto left = ask(u << 1, l, r);
    auto right = ask(u << 1 | 1, l, r);
    Node ans;
    pushup(ans, left, right);
    return ans;
}

int main() {
    cin.tie(0);
    ios::sync_with_stdio(false);
    cin >> n >> m;
    for (int i = 1; i <= n; ++i) cin >> a[i];
    build(1, 1, n);
    
    char op;
    int l, r;
    while (m--) {
        cin >> op >> l >> r;
        if (op == 'C') {
            LL d;
            cin >> d;
            modify(1, l, d);
            if (r + 1 <= n) modify(1, r + 1, -d);
        } else {
            auto left = ask(1, 1, l);
            Node right({0, 0, 0, 0, 0});
            if (l + 1 <= r) right = ask(1, l + 1, r);
            cout << abs(gcd(left.sum, right.d)) << endl;
        }
    }
}

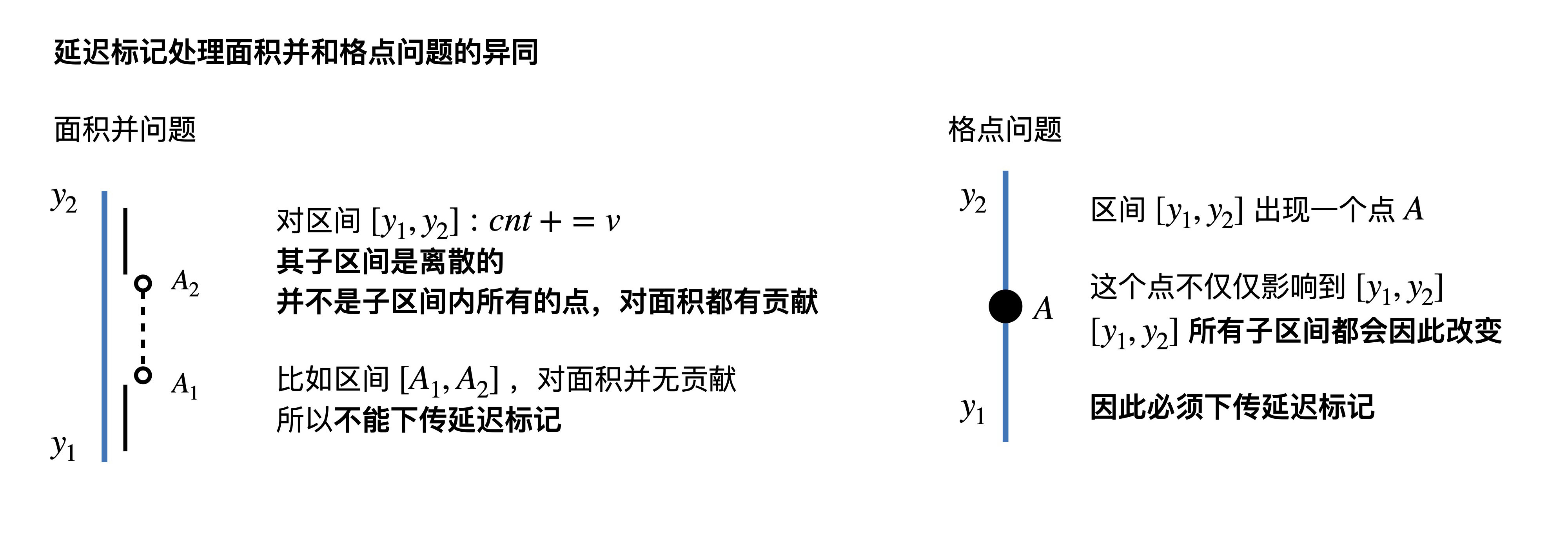
区间修改延迟标记、pushdown操作

在线段树的 “区间查询” 指令中, 每当遇到被询问区间 [l,r][l, r] 完全覆盖的节点时, 可以立即把该节点上存储的信息作为候选答案返回。我们已经证明, 被询问区间 [l,r][l, r] 在线段树上会被分成 O(log⁡N)O(\log N) 个小区间 (节点), 从而在 O(log⁡N)O(\log N) 的时间内求出答案。不过, 在 “区间修改” 指令中, 如果某个节点被修改区间 [l,r][l, r] 完全覆盖, 那么以该节点为根的整棵子树中的所有节点存储的信息都会发生变化, 若逐一进行更新, 将使得一次区间修改指令的时间复杂度增加到 O(N)O(N), 这是我们不能接受的。

试想, 如果我们在一次修改指令中发现节点 pp 代表的区间 [pl,pr]\left[p_{l}, p_{r}\right] 被修改区间 [l,r][l, r] 完全覆盖, 并且逐一更新了子树 pp 中的所有节点, 但是在之后的查询指令中却根本没有用到 [l,r][l, r] 的子区间作为候选答案, 那么更新 pp 的整棵子树就是徒劳的。

换言之, 我们在执行修改指令时, 同样可以在 l≤pl≤pr≤rl \leq p_{l} \leq p_{r} \leq r 的情况下立即返回, 只不过在回溯之前向节点 pp 增加一个标记, 标识 “该节点曾经被修改, 但其子节点尚未被更新”。

如果在后续的指令中, 需要从节点 pp 向下递归, 我们再检查 pp 是否具有标记。若有标记, 就根据标记信息更新 pp 的两个子节点, 同时为 pp 的两个子节点增加标记, 然后清除 pp 的标记。

也就是说, 除了在修改指令中直接划分成的 O(log⁡N)O(\log N) 个节点之外, 对任意节点的修改都延迟到 “在后续操作中递归进入它的父节点时” 再执行。这样一来, 每条查询或修改指令的时间复杂度都降低到了 O(log⁡N)O(\log N) 。这些标记被称为 “延迟标记”。延迟标记提供了线段树中从上往下传递信息的方式 。这种 “延迟” 也是设计算法与解决问题的一个重要思路。

有一种称为 “标记永久化” 的技巧, 可以不下传标记, 而是在查询时累计递归经过的所有标记产生的影 响。这种做法局限性非常大, 对线段树维护的信息和标记的性质有特殊要求, 仅在二维线段树和可持久化 线段树难以下传标记的情况下有所应用, 超出了我们的讨论范围。

243. 一个简单的整数问题2

给定一个长度为 NN 的数列 AA，以及 MM 条指令，每条指令可能是以下两种之一：

  1. C l r d，表示把 A[l],A[l+1],…,A[r]A[l],A[l+1],…,A[r] 都加上 dd。
  2. Q l r，表示询问数列中第 l∼rl \sim r 个数的和。

对于每个询问，输出一个整数表示答案。

输入格式

第一行两个整数 N,MN,M。

第二行 NN 个整数 A[i]A[i]。

接下来 MM 行表示 MM 条指令，每条指令的格式如题目描述所示。

输出格式

对于每个询问，输出一个整数表示答案。

每个答案占一行。

数据范围

1≤N,M≤1051 \le N,M \le 10^5,
∣d∣≤10000|d| \le 10000,
∣A[i]∣≤109|A[i]| \le 10^9

输入样例：

1
2
3
4
5
6
7
10 5
1 2 3 4 5 6 7 8 9 10
Q 4 4
Q 1 10
Q 2 4
C 3 6 3
Q 2 4

输出样例：

1
2
3
4
4
55
9
15

算法分析

在上一节中我们用树状数组解决了该问题, 本节我们改用线段树来求解。除了左右端点 l,rl, r 以外, 线段树的每个节点上保存了 sumsum (区间和)、 adda d d (增量延迟标记) 两个值。建树、查询和修改的框架仍然不变, spreadspread 函数实现了延迟标记的向下传递。

需要指出的是, 延迟标记的含义为 “该节点曾经被修改, 但其子节点尚未被更新”, 即延迟标记标识的是子节点等待更新的情况。因此,一个节点被打上 “延迟标记” 的同时, 它自身保存的信息应该已经被修改完毕。读者在编写代码时, 一定要注意 “更新信息”与 “打标记” 之间的关系, 避免出现错误。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;

const int SIZE = 100010;
struct SegmentTree {
  int l, r;
  long long sum, add;
#define l(x) tree[x].l
#define r(x) tree[x].r
#define sum(x) tree[x].sum
#define add(x) tree[x].add
} tree[SIZE * 4];
int a[SIZE], n, m;

void build(int p, int l, int r) { // No.p, [l,r]
  l(p) = l, r(p) = r;
  if (l == r) {
    sum(p) = a[l];
    return;
  }
  int mid = (l + r) / 2;
  build(p * 2, l, mid);
  build(p * 2 + 1, mid + 1, r);
  sum(p) = sum(p * 2) + sum(p * 2 + 1);
}

void spread(int p) {
  if (add(p)) { // 节点 p 有标记
    sum(p * 2) += add(p) * (r(p * 2) - l(p * 2) + 1); // 更新左子节点信息
    sum(p * 2 + 1) += add(p) * (r(p * 2 + 1) - l(p * 2 + 1) + 1); // 更新右子节点
    add(p * 2) += add(p); // 给左子节点打延迟标记
    add(p * 2 + 1) += add(p); // 给右子节点打延迟标记
    add(p) = 0; // 清除 p 的标记
  }
}

void change(int p, int l, int r, int z) {
  if (l <= l(p) && r >= r(p)) { // 完全覆盖
    sum(p) += (long long)z * (r(p) - l(p) + 1); // 更新节点信息
    add(p) += z; // 给节点打延迟标记
    return;
  }
  spread(p); // 下传延迟标记
  int mid = (l(p) + r(p)) / 2;
  if (l <= mid) change(p * 2, l, r, z);
  if (r > mid) change(p * 2 + 1, l, r, z);
  sum(p) = sum(p * 2) + sum(p * 2 + 1);
}

long long ask(int p, int l, int r) {
  if (l <= l(p) && r >= r(p)) return sum(p);
  spread(p); // 下传延迟标记
  int mid = (l(p) + r(p)) / 2;
  long long ans = 0;
  if (l <= mid) ans += ask(p * 2, l, r);
  if (r > mid) ans += ask(p * 2 + 1, l, r);
  return ans;
}

int main() {
  cin >> n >> m;
  for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
  build(1, 1, n);
  while (m--) {
    char op[2];
    int x, y, z;
    scanf("%s%d%d", op, &x, &y);
    if (op[0] == 'C') {
      scanf("%d", &z);
      change(1, x, y, z);
    } else
      printf("%I64d\n", ask(1, x, y));
  }
}

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
#include <iostream>
using namespace std;
using LL = long long;

const int N = 1e5 + 10;

int n, m;
LL a[N];
struct Node {
    int l, r;
    LL sum, add;
} tr[4 * N];

void pushup(Node &u, Node &l, Node &r) {
    u.sum = l.sum + r.sum;
}

void pushup(int u) {
    pushup(tr[u], tr[u << 1], tr[u << 1 | 1]);
}

void pushdown(int u) {
    auto &root = tr[u], &l = tr[u << 1], &r = tr[u << 1 | 1];
    if (root.add) {
        l.add += root.add;
        l.sum += (LL)(l.r - l.l + 1) * root.add;
        r.add += root.add;
        r.sum += (LL)(r.r - r.l + 1) * root.add;
        root.add = 0;
    }
}

void build(int u, int l, int r) {
    if (l == r) {
        tr[u] = {l, r, a[l], 0};
        return;
    } 
    
    tr[u] = {l ,r};
    int mid = l + r >> 1;
    build(u << 1, l , mid);
    build(u << 1 | 1, mid + 1, r);
    pushup(u);        
}

void modify_add(int u, int l, int r, int d) {
    if (l <= tr[u].l && tr[u].r <= r) {
        tr[u].sum += (LL)(tr[u].r - tr[u].l + 1) * d;
        tr[u].add += d;
        return;
    } 
    
    pushdown(u);
    int mid = tr[u].l + tr[u].r >> 1;
    if (l <= mid) modify_add(u << 1, l, r, d);
    if (r > mid) modify_add(u << 1 | 1, l, r ,d);
    pushup(u);
}

LL ask(int u, int l, int r) {
    if (l <= tr[u].l && tr[u].r <= r) return tr[u].sum;
    
    pushdown(u);
    int mid = tr[u].l + tr[u].r >> 1;
    LL sum = 0;
    if (l <= mid) sum += ask(u << 1, l, r);
    if (r > mid) sum += ask(u << 1 | 1, l, r);
    return sum;
}

int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; ++i) cin >> a[i];
    build(1, 1, n);
    
    char op;
    int l, r, d;
    while (m--) {
        cin >> op >> l >> r;
        if (op == 'C') {
            cin >> d;
            modify_add(1, l, r, d);
        } else {
            cout << ask(1, l, r) << endl;
        }
    }
}

1277. 维护序列

老师交给小可可一个维护数列的任务，现在小可可希望你来帮他完成。

有长为 NN 的数列，不妨设为 a1,a2,…,aNa_1,a_2,…,a_N。

有如下三种操作形式：

  1. 把数列中的一段数全部乘一个值；
  2. 把数列中的一段数全部加一个值；
  3. 询问数列中的一段数的和，由于答案可能很大，你只需输出这个数模 PP 的值。

输入格式

第一行两个整数 NN 和 PP；

第二行含有 NN 个非负整数，从左到右依次为 a1,a2,…,aNa_1,a_2,…,a_N；

第三行有一个整数 MM，表示操作总数；

从第四行开始每行描述一个操作，输入的操作有以下三种形式：

  • 操作 11：1 t g c，表示把所有满足 t≤i≤gt \le i \le g 的 aia_i 改为 ai×ca_i \times c；
  • 操作 22：2 t g c，表示把所有满足 t≤i≤gt \le i \le g 的 aia_i 改为 ai+ca_i + c；
  • 操作 33：3 t g，询问所有满足 t≤i≤gt \le i \le g 的 aia_i 的和模 PP 的值。

同一行相邻两数之间用一个空格隔开，每行开头和末尾没有多余空格。

输出格式

对每个操作 33，按照它在输入中出现的顺序，依次输出一行一个整数表示询问结果。

数据范围

1≤N,M≤1051 \le N,M \le 10^5,
1≤t≤g≤N1 \le t \le g \le N,
0≤c,ai≤1090 \le c,a_i \le 10^9,
1≤P≤1091 \le P \le 10^9

输入样例：

1
2
3
4
5
6
7
8
7 43
1 2 3 4 5 6 7
5
1 2 5 5
3 2 4
2 3 7 9
3 1 3
3 4 7

输出样例：

1
2
3
2
35
8

样例解释

初始时数列为 {1,2,3,4,5,6,7}\lbrace 1,2,3,4,5,6,7 \rbrace；

经过第 11 次操作后，数列为 {1,10,15,20,25,6,7}\lbrace 1,10,15,20,25,6,7 \rbrace；

对第 22 次操作，和为 10+15+20=4510+15+20=45，模 4343 的结果是 22；

经过第 33 次操作后，数列为 {1,10,24,29,34,15,16}\lbrace 1,10,24,29,34,15,16 \rbrace；

对第 44 次操作，和为 1+10+24=351+10+24=35，模 4343 的结果是 3535；

对第 55 次操作，和为 29+34+15+16=9429+34+15+16=94，模 4343 的结果是 88。

算法分析

1.区间修改 - 乘 加
3.区间查询

存储信息：
1.区间范围l,r
2.加的懒标记add
3.乘的懒标记mul
4.区间总和sum

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
对于x
若对懒标记的处理是先加再乘
    若此次操作为乘上一个数c
        可以表示为 (n + add) * mul * c 即 (n + X) * X 的形式
    若此次操作为加上一个数c
        (n + add) * mul + c 不能写成 (n + X ) * X的形式
        -> 无法更新新的懒标记

若对懒标记的处理是先乘再加
    若此次操作是加上一个数c
        可以表示为n * mul + add + c
        -> 此时新的add即为add + c
    若此次操作是乘上一个数c
        可以表示为n * mul * c + add * c
        -> 此时新的add即为add * c，新的mul即为mul * c 

-> 故先乘再加，以便更新懒标记

可以把乘和加的操作都看成 x * c + d
    -> 若是乘法，d为0
    -> 若是加法，c为1

若当前x的懒标记为add和mul
    -> 操作可以写成(x * mul + add) * c + d
    -> 即x * (mul * c) + (add * c + d)
    -> 新的mul为(mul * c)，新的add为(add * c + d)

注意：乘的懒标记初始为1

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
#include <iostream>
using namespace std;
using LL = long long;

const int N = 1e5 + 10;

int n, p, m;
int a[N];

struct Node {
    int l, r;
    LL sum = 0, mul = 1, add = 0;
} tr[N * 4];

void pushup(Node &u, Node &ls, Node &rs) {
    u.sum = (ls.sum + rs.sum) % p;
}

void pushup(int u) {
    pushup(tr[u], tr[u << 1], tr[u << 1 | 1]);
}

void calc(Node& u, int mul, int add) { // 先处理乘，后处理加
    u.sum = (u.sum * mul + 1LL * (u.r - u.l + 1) * add) % p;
    u.mul = u.mul * mul % p;
    u.add = (u.add * mul + add) % p;
}

void pushdown(Node &u, Node &ls, Node &rs) {
    calc(ls, u.mul, u.add);
    calc(rs, u.mul, u.add);
    u.add = 0;
    u.mul = 1;
}

void pushdown(int u) {
    pushdown(tr[u], tr[u << 1], tr[u << 1 | 1]);
}

void build(int u, int l, int r) {
    if (l == r) {
        tr[u] = {l, r, a[l], 1, 0};
        return;
    }
    
    tr[u] = {l, r};
    int mid = l + r >> 1;
    build(u << 1, l, mid);
    build(u << 1 | 1, mid + 1, r);
    pushup(u);
}

void modify(int u, int l, int r, int mul, int add) {
    if (l <= tr[u].l && tr[u].r <= r) {
        calc(tr[u], mul, add);
        return;
    }
    
    pushdown(u);
    int mid = tr[u].l + tr[u].r >> 1;
    if (l <= mid) modify(u << 1, l, r, mul, add);
    if (r > mid) modify(u << 1 | 1, l, r, mul, add);
    pushup(u);
}

int ask(int u, int l, int r) {
    if (l <= tr[u].l && tr[u].r <= r) return tr[u].sum;
    
    pushdown(u);
    int mid = tr[u].l + tr[u].r >> 1;
    LL sum = 0;
    if (l <= mid) sum += ask(u << 1, l, r);
    if (r > mid) sum += ask(u << 1 | 1, l, r);
    return sum % p;
}

int main() {
    cin.tie(0);
    ios::sync_with_stdio(false);
    cin >> n >> p;
    for (int i = 1; i <= n; ++i) cin >> a[i];
    build(1, 1, n);
    
    cin >> m;
    while (m--) {
        int op, l, r, c;
        cin >> op >> l >> r;
        if (op == 1) {
            cin >> c;
            modify(1, l, r, c, 0);
        } else if (op == 2) {
            cin >> c;
            modify(1, l, r, 1, c);
        } else {
            cout << ask(1, l, r) << endl;
        }
    }
}

扫描线

247. 亚特兰蒂斯

有几个古希腊书籍中包含了对传说中的亚特兰蒂斯岛的描述。

其中一些甚至包括岛屿部分地图。

但不幸的是，这些地图描述了亚特兰蒂斯的不同区域。

您的朋友 Bill 必须知道地图的总面积。

你自告奋勇写了一个计算这个总面积的程序。

输入格式

输入包含多组测试用例。

对于每组测试用例，第一行包含整数 nn，表示总的地图数量。

接下来 nn 行，描绘了每张地图，每行包含四个数字 x1,y1,x2,y2x_1,y_1,x_2,y_2（不一定是整数），(x1,y1)(x_1,y_1) 和 (x2,y2)(x_2,y_2) 分别是地图的左上角位置和右下角位置。

注意，坐标轴 xx 轴从上向下延伸，yy 轴从左向右延伸。

当输入用例 n=0n=0 时，表示输入终止，该用例无需处理。

输出格式

每组测试用例输出两行。

第一行输出 Test case #k，其中 kk 是测试用例的编号，从 11 开始。

第二行输出 Total explored area: a，其中 aa 是总地图面积（即此测试用例中所有矩形的面积并，注意如果一片区域被多个地图包含，则在计算总面积时只计算一次），精确到小数点后两位数。

在每个测试用例后输出一个空行。

数据范围

1≤n≤100001 \le n \le 10000,
0≤x1<x2≤1000000 \le x_1 < x_2 \le 100000,
0≤y1<y2≤1000000 \le y_1 < y_2 \le 100000
注意，本题 nn 的范围上限加强至 1000010000。

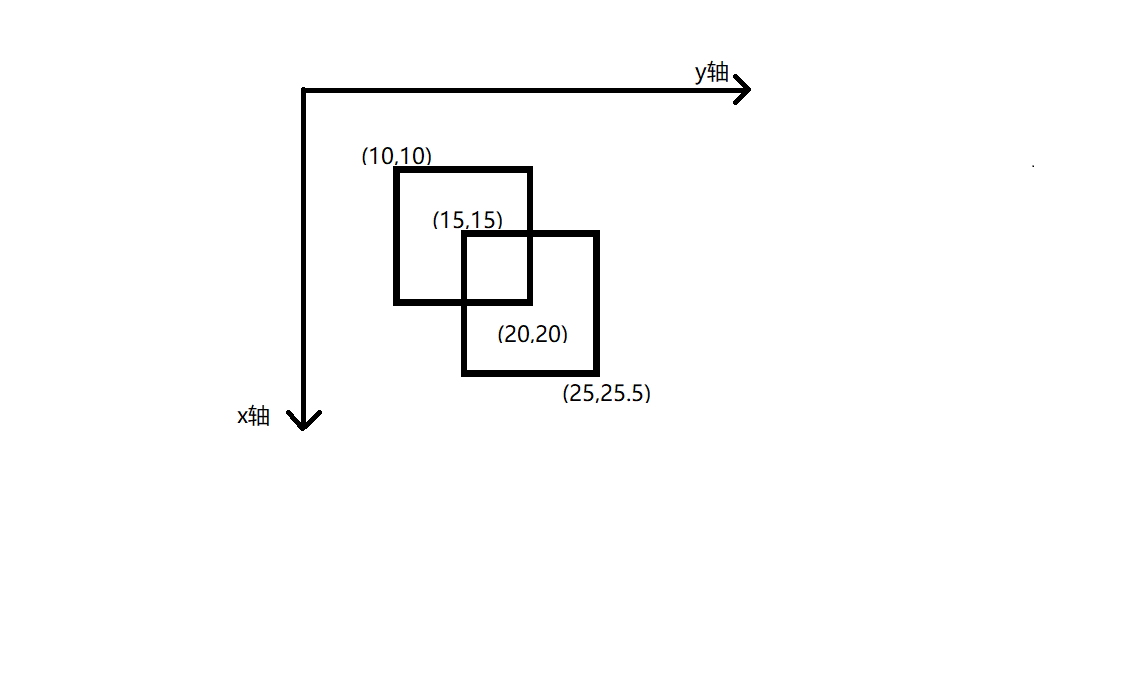
输入样例：

1
2
3
4
2
10 10 20 20
15 15 25 25.5
0

输出样例：

1
2
Test case #1
Total explored area: 180.00

样例解释

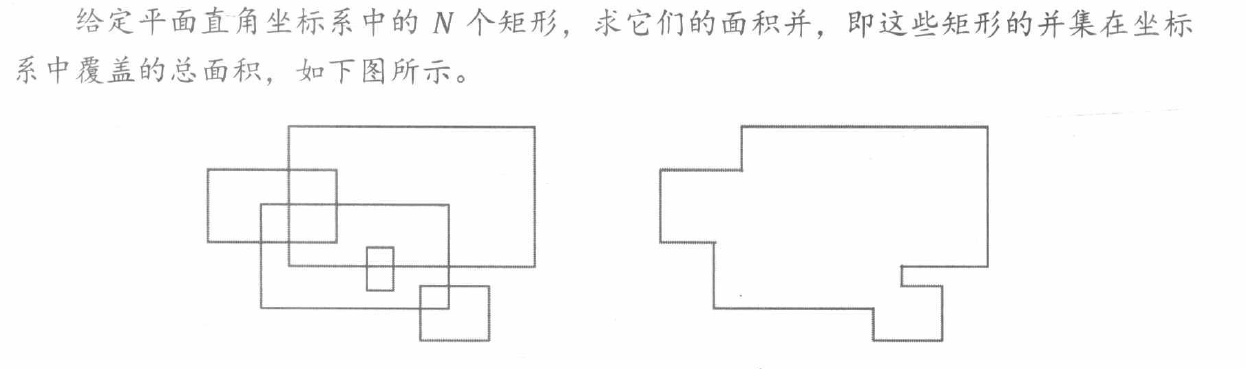
样例所示地图覆盖区域如下图所示，两个矩形区域所覆盖的总面积，即为样例的解。

算法分析

试想, 如果我们用一条坚直直线从左到右扫过整个坐标系, 那么直线上被并集图形覆盖的长度只会在每个矩形的左右边界处发生变化。

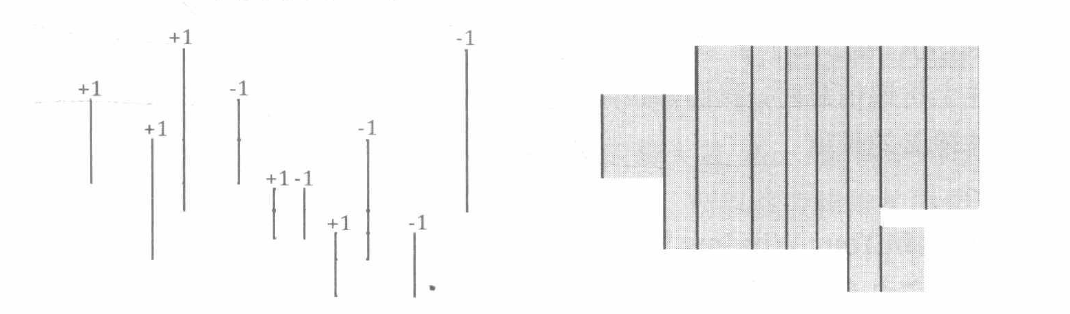
换言之, 整个并集图形可以被分成 2∗N2 * N 段, 每一段在直线上覆盖的长度 (记为 LL ) 是固定的, 因此该段的面积就是 L∗WL*W , WW 是该段的宽度, 各段面积之和即为所求。这条直线就被称为扫描线, 这种解题思路被称为扫描线法。

具体来说, 我们可以取出 NN 个矩形的左右边界。若一个矩形的两个对角顶点坐标 为 (x1,y1)\left(x_{1}, y_{1}\right) 和 (x2,y2)\left(x_{2}, y_{2}\right), 不妨设 x1<x2,y1<y2x_{1}<x_{2}, y_{1}<y_{2}, 则左边界记为四元组 (x1,y1,y2,1)\left(x_{1}, y_{1}, y_{2}, 1\right), 右边界记为四元组 (x2,y1,y2,−1)\left(x_{2}, y_{1}, y_{2},-1\right) 。把这 2N2 N 个四元组按照 xx 递增排序, 如下图所示。

注意到本题中的 yy 坐标范围较大且不一定是整数, 我们先把输入数据中出现的所有 yy 坐标放入一个数组, 排序、去重, 完成离散化。设 val(y)val(y) 表示 yy 被离散化之后映射到的整数值, raw(i)raw(i) 表示整数值 ii 对应的原始 yy 坐标值。

在离散化后, 若有 MM 个不同的 yy 坐标值, 分别对应 raw(1),raw(2),⋯ ,raw(M)raw(1), raw(2), \cdots, raw(M), 则扫描线至多被分成 M−1M-1 段, 其中第 ii 段为区间 [raw(i),raw(i+1)][raw(i),raw(i+1)] 。建立数组 cc, 用 c[i]c[i] 记录扫描线上第 ii 段被覆盖的次数。起初 cc 数组中的元素全为 0 。

逐一扫描排序后的 2N2 N 个四元组, 设当前四元组为 (x,y1,y2,k)\left(x, y_{1}, y_{2}, k\right) 。我们把数组 cc 中 c[val(y1)],c[val(y1)+1],⋯ ,c[val(y2)−1]c\left[val\left(y_{1}\right)\right], c\left[val\left(y_{1}\right)+1\right], \cdots, c\left[val\left(y_{2}\right)-1\right] 这些值都加 kk, 相当于覆盖了 [y1,y2]\left[y_{1}, y_{2}\right] 这个区间。此时, 如果下一个四元组的横坐标为 x2x_{2}, 则扫描线从 xx 扫到 x2x_{2} 的过程中, 被覆盖的长度就固定为 ∑c[i]>0(raw(i+1)−raw(i))\sum_{c[i]>0}(raw(i+1)-raw(i)), 即数组 cc 中至少被覆盖一次的 “段” 的总长度。于是, 我们就让最终的答案 ans 累加上 (x2−x)∗∑c[i]>0(raw(i+1)−raw(i)\left(x_{2}-x\right) * \sum_{c[i]>0}(raw(i+ 1)-raw(i) 。

对于每个四元组, 采用朴素算法在 cc 数组上执行修改与统计, 即可在 O(N2)\mathrm{O}\left(N^{2}\right) 的时间内求出并集图形的面积。

值得说明的是, 四元组中的 y1,y2y_{1}, y_{2} 都是坐标, 是一个“点”。我们需要维护的是扫描线上每一段被覆盖的次数及其长度, 对 “点” 的覆盖次数进行统计是没有意义的。因此, 我们把 cc 数组中的每个值 c[i]c[i] 定义成扫描线上一个区间的覆盖次数, 四元组 (x,y1,y2,k)\left(x, y_{1}, y_{2}, k\right) 对 c[val(y1)∼val(y2)−1]c\left[val\left(y_{1}\right) \sim val\left(y_{2}\right)-1\right] 产生影响。读者在解题时一定要多加留意此类边界情况。

另外, 我们可以用线段树维护 cc 数组, 把算法优化到 O(Nlog⁡N)O(N \log N) 。

在本题中, 我们只关心整个扫描线 (线段树根节点) 上被矩形覆盖的长度。而且, 因为四元组 (x,y1,y2,1)\left(x, y_{1}, y_{2}, 1\right) 和 (x,y1,y2,−1)\left(x, y_{1}, y_{2},-1\right) 成对出现, 所以线段树区间修改也是成对出现的。在这种特殊情形下, 我们没有必要下传延迟标记, 可以采用更为简单的做法。

除左右端点 l,rl, r 之外, 在线段树的每个节点上维护两个值：该节点代表的区间被矩形覆盖的长度 lenl e n, 该节点自身被覆盖的次数 cntc n t 。最初, 二者均为 0 。

对于一个四元组 (x,y1,y2,k)\left(x, y_{1}, y_{2}, k\right), 我们在 [val(y1),val(y2)−1]\left[val\left(y_{1}\right), val\left(y_{2}\right)-1\right] 上执行区间修改。该区间被线段树划分成 O(log⁡N)O(\log N) 个节点, 我们把这些节点的 cntc n t 都加 kk 。

对于线段树中任意一个节点 [l,r][l, r], 若 cnt>0c n t>0, 则 len 等于 raw(r+1)−raw(l)raw(r+1)-raw(l) 。否则, 该点 lenlen 等于两个子节点的 lenlen 之和。在一个节点的 cntcnt 值被修改, 以及线段树从下往上传递信息时, 我们都按照该方法更新 lenlen 值。根节点的 lenlen 值就是整个 扫描线上被覆盖的长度。

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
#include <iostream>
#include <vector>
#include <algorithm>
#include <iomanip>
using namespace std;

const int N = 1e5 + 10;

int n;

// 存储的区间
struct Range {
    double x, y1, y2;
    int k;
    bool operator< (const Range &t) const {
        return x < t.x;
    }
} range[N * 2];

// 线段树节点
struct Node {
    int l, r;
    int cnt;
    double len;
} tr[N * 2 * 4];

// 离散化操作
vector<double> ys;
// 直接用哈希表查询：原始值经过离散化映射到的整数值，即ys数组的下标
unordered_map<double, int> idx; 
// 用二分查找查询：原始值经过离散化映射到的整数值，即ys数组的下标
int findIdx(double y) { 
    return lower_bound(ys.begin(), ys.end(), y) - ys.begin();
}

// 线段树部分

void pushup(Node &u, Node &ls, Node &rs) {
    if (u.cnt) {
        u.len = ys[u.r + 1] - ys[u.l];
    } else if (u.l != u.r) {
        u.len = ls.len + rs.len;
    } else if (u.l == u.r){
        u.len = 0;
    }
}

void pushup(int u) {
    pushup(tr[u], tr[u << 1], tr[u << 1 | 1]);
}

void build(int u, int l, int r) {
    if (l == r) {
        tr[u] = {l, r, 0, 0};
        return; 
    }
    
    tr[u] = {l, r};
    int mid = l + r >> 1;
    build(u << 1, l, mid);
    build(u << 1 | 1, mid + 1, r);
    pushup(u);
}

void modify(int u, int l, int r, int d) {
    if (l <= tr[u].l && tr[u].r <= r) {
        tr[u].cnt += d;
        pushup(u); // d 可能是负数，使得cnt = 0，需要 pushup 计算len
        return;
    }
    
    int mid = tr[u].l + tr[u].r >> 1;
    if (l <= mid) modify(u << 1, l, r, d);
    if (r > mid) modify(u << 1 | 1, l, r, d);
    pushup(u);
}

int main() {
    int T = 1;
    while (cin >> n, n) {
        ys.clear();
        
        for (int i = 0; i < n; ++i) {
            double x1, y1, x2, y2;
            cin >> x1 >> y1 >> x2 >> y2;
            
            // 存储每个线段区间
            range[i << 1] = {x1, y1, y2, 1};
            range[i << 1 | 1] = {x2, y1, y2, -1};
            
            // 纵坐标 y 离散化操作
            ys.push_back(y1);
            ys.push_back(y2);
        }
        
        //离散化操作
        sort(ys.begin(), ys.end());
        ys.erase(unique(ys.begin(), ys.end()), ys.end());
        for (int i = 0; i < ys.size(); ++i) idx[ys[i]] = i;
        int m = ys.size(); // m 是离散化后 y 坐标个数
        
        
        // y 坐标离散化为：[0, m - 1]，仅使用 [0, m - 2], 其中 i 表示区间[i, i + 1] 
        // 区间 [l, r] 实际表示区间 [ys[l], ys[l + 1]], [ys[l + 1], [ys[l + 2]]...[[ys[r], ys[r + 1]]
        // 即 ys[l] ~ ys[r + 1]
        build(1, 0, m - 2); 
        
        sort(range, range + 2 * n); // 所有线段区间排序
        
        double ans = 0;
        
        for (int i = 0; i < 2 * n; ++i) {
            if (i) ans += tr[1].len * (range[i].x - range[i - 1].x);
            
            // 要修改实际区间范围 [y1, y2] 上的cnt
            // 对应离散化区间范围： idx[y1] ~ idx[y2], 用 [idx[y1], idx[y2] - 1] 表示
            modify(1, idx[range[i].y1], idx[range[i].y2] - 1, range[i].k);
        }
        
        cout << "Test case #" << T++ << endl;
        cout << "Total explored area: " << fixed << setprecision(2) << ans << endl;
        cout << endl;
    }
}

248. 窗内的星星

在一个天空中有很多星星（看作平面直角坐标系），已知每颗星星的坐标和亮度（都是整数）。

求用宽为 WW、高为 HH 的矩形窗口（W,HW,H 为正整数）能圈住的星星的亮度总和最大是多少。（矩形边界上的星星不算）

输入格式

输入包含多组测试用例。

每个用例的第一行包含 33 个整数：n，W，Hn，W，H，表示星星的数量，矩形窗口的宽和高。

然后是 nn 行，每行有 33 个整数：x，y，cx，y，c，表示每个星星的位置 (x，y)(x，y) 和亮度。

没有两颗星星在同一点上。

输出格式

每个测试用例输出一个亮度总和最大值。

每个结果占一行。

数据范围

1≤n≤100001 \le n \le 10000,
1≤W,H≤10000001 \le W,H \le 1000000,
0≤x,y<2310 \le x,y < 2^{31}

输入样例：

1
2
3
4
5
6
7
8
3 5 4
1 2 3
2 3 2
6 3 1
3 5 4
1 2 3
2 3 2
5 3 1

输出样例：

1
2
5
6

算法分析

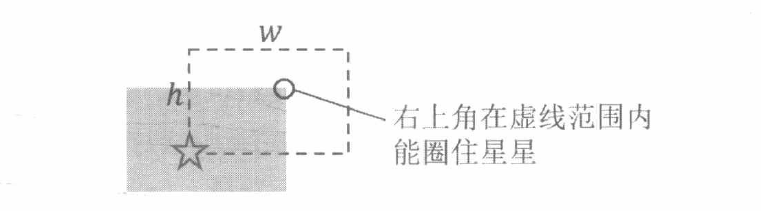
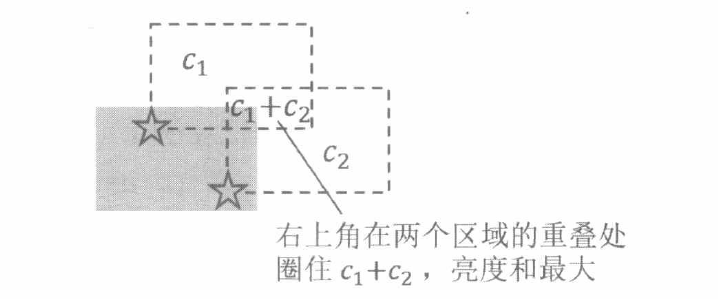
因为矩形的大小固定, 所以矩形可以由它的任意一个顶点唯一确定。我们可以考虑把矩形的右上角顶点放在什么位置, 圈住的星星亮度总和最大。

对于一个星星 (x,y,c)(x, y, c), 其中 x,yx, y 为坐标, cc 为亮度, “能圈住这颗星星的矩形右上角顶点坐标的范围” 如下图所示。该范围也是一个矩形, 左下角顶点为 (x,y)(x, y), 右上角顶点为 (x+w,y+h)(x+w, y+h) 。为了避免歧义, 在接下来的讨论中, 我们用 “区域” 一 词来代指这个范围。

题目中说 “矩形边界上的星星不算” 。为了处理这种边界情况, 不妨把所有星星向左、向下各移动 0.50.5 的距离, 坐标从 (x,y)(x, y) 变为 (x−0.5,y−0.5)(x-0.5, y-0.5) 。在此基础上, 不妨假设圈住星星的矩形顶点坐标都是整数。于是, 上图虚线 “区域” 的左下角可看作 (x,y)(x, y), 右上角可看作 (x+w−1,y+h−1)(x+w-1, y+h-1), 边界也算在内。容易证明这些假设不会影响答案。

此时, 问题转化为: 平面上有若干个区域, 每个区域都带有一个权值, 求在哪个坐 标上重叠的区域权值和最大。其中, 每一个区域都是由一颗星星产生的, 权值等于星星 的亮度, 把原问题中的矩形右上角放在该区域中, 就能圈住这颗星星。

在转化后的问题中, 我们使用扫描线算法, 取出每个区域的左右边界, 保存成两个四元组 (x,y,y+h−1,c)(x, y, y+h-1, c) 和 (x+w,y,y+h−1,−c)(x+w, y, y+h-1,-c) 。把这些四元组按照横坐标 (第一维的值) 排序。

同时, 关于纵坐标建立一棵线段树, 维护区间最大值 datd a t, 起初全为零。因为我们已经平移了星星的坐标, 并假设矩形只能放在整点上, 所以线段树维护的相当于是若干个数值 (纵坐标整点上的权值和) 构成的序列。逐一扫描每个四元组 (x,y1,y2,c)\left(x, y_{1}, y_{2}, c\right), 在线段树中执行区间修改 (可用延迟标记实现), 把 [y1,y2]\left[y_{1}, y_{2}\right] 中的每个数都加 cc, 然后用根节点的 dat 值更新答案即可。

Solution

动态开点与线段树合并