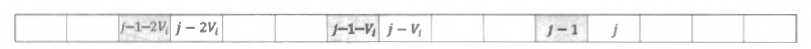参考《算法竞赛进阶指南》 、AcWing题库
单调队列优化DP
“单调栈” 和 “单调队列” 这两种思想的本质都是借助单调性, 及时排除不可能的决策, 保持候选集合的高度有效性和秩序性。仔细回顾 “最大子序和” 这道例题, 该问题的答案可以形式化表述为:
a n s = max 1 ≤ i ≤ N { S [ i ] − min i − M ≤ j ≤ i − 1 { S [ j ] } } a n s=\max _{1 \leq i \leq N}\left\{S[i]-\min _{i-M \leq j \leq i-1}\{S[j]\}\right\}
an s = 1 ≤ i ≤ N max { S [ i ] − i − M ≤ j ≤ i − 1 min { S [ j ]} }
此处的 i i i j j j i ∈ [ 1 , N ] i \in[1, N] i ∈ [ 1 , N ] i i i j j j [ i − M , i − 1 ] [i-M, i-1] [ i − M , i − 1 ] [ i − M + 1 , i ] [i-M+1, i] [ i − M + 1 , i ] j = i j=i j = i j = i − M j=i-M j = i − M
类比 “最大子序和”一题的思想, 尝试解答下面几道例题。
题目描述
有 N N N M M M
第 i i i S i S_i S i L i L_i L i P i P_i P i
不同工匠的 S i S_i S i
请问如何安排能使工匠们获得的总报酬最多。
输入格式
第一行包含两个整数 N N N M M M
接下来 M M M L i , P i , S i L_i,P_i,S_i L i , P i , S i
输出格式
输出一个整数,表示结果。
数据范围
1 ≤ N ≤ 16000 1 \le N \le 16000 1 ≤ N ≤ 16000 1 ≤ M ≤ 100 1 \le M \le 100 1 ≤ M ≤ 100 1 ≤ P i ≤ 10000 1 \le P_i \le 10000 1 ≤ P i ≤ 10000
输入样例 :
1 2 3 4 5 8 4 3 2 2 3 2 3 3 3 5 1 1 7
输出样例 :
算法分析
先把所有工匠按照 S i S_{i} S i
设 F [ i , j ] F[i, j] F [ i , j ] i i i j j j
第 i i i F [ i , j ] = F [ i − 1 , j ] F[i, j]=F[i-1, j] F [ i , j ] = F [ i − 1 , j ]
第 j j j F [ i , j ] = F [ i , j − 1 ] F[i, j]=F[i, j-1] F [ i , j ] = F [ i , j − 1 ]
第 i i i k + 1 k+1 k + 1 j j j L i L_{i} L i S i S_{i} S i k + 1 ≤ S i ≤ j k+1 \leq S_{i} \leq j k + 1 ≤ S i ≤ j j − k ≤ L i j-k \leq L_{i} j − k ≤ L i
F [ i , j ] = max j − L i ≤ k ≤ S i − 1 { F [ i − 1 , k ] + P i ∗ ( j − k ) } , 其中 j ≥ S i F[i, j]=\max _{j-L_{i} \leq k \leq S_{i}-1}\left\{F[i-1, k]+P_{i} *(j-k)\right\} \text {, 其中 } j \geq S_{i}
F [ i , j ] = j − L i ≤ k ≤ S i − 1 max { F [ i − 1 , k ] + P i ∗ ( j − k ) } , 其中 j ≥ S i
我们重点来看这个方程如何优化。首先, 我们多次提到, 在考虑内层循环 j j j k k k i i i
P i ∗ j P_{i} * j P i ∗ j i i i j j j F [ i − 1 , k ] − P i ∗ k F[i-1, k]-P_{i} * k F [ i − 1 , k ] − P i ∗ k i i i k k k
状态转移方程可改写为:
F [ i , j ] = P i ∗ j + max j − L i ≤ k < S i − 1 { F [ i − 1 , k ] − P i ∗ k } , 其中 j ≥ S i F[i, j]=P_{i} * j+\max _{j-L_{i} \leq k<S_{i}-1}\left\{F[i-1, k]-P_{i} * k\right\} \text {, 其中 } j \geq S_{i}
F [ i , j ] = P i ∗ j + j − L i ≤ k < S i − 1 max { F [ i − 1 , k ] − P i ∗ k } , 其中 j ≥ S i
当 j j j k k k S i − 1 S_{i}-1 S i − 1 j − L i j-L_{i} j − L i k 1 k_{1} k 1 k 2 k_{2} k 2 k 1 < k 2 ≤ k_{1}<k_{2} \leq k 1 < k 2 ≤ s i − 1 s_{i}-1 s i − 1
因为 k 2 k_{2} k 2 k 1 k_{1} k 1 j j j k 1 k_{1} k 1 k 2 k_{2} k 2 [ j − L i , S i − 1 ] \left[j-L_{i}, S_{i}-1]\right. [ j − L i , S i − 1 ] F [ i − 1 , k 1 ] − P i ∗ k 1 ≤ F [ i − 1 , k 2 ] − P i ∗ k 2 F\left[i-1, k_{1}\right]-P_{i} * k_{1} \leq F\left[i-1, k_{2}\right]-P_{i} * k_{2} F [ i − 1 , k 1 ] − P i ∗ k 1 ≤ F [ i − 1 , k 2 ] − P i ∗ k 2 k 2 k_{2} k 2 k 1 k_{1} k 1 k 1 k_{1} k 1 k 1 k_{1} k 1
综上所述, 我们可以维护一个决策点 k k k F [ i − 1 , k ] − P i ∗ k F[i-1, k]-P_{i} * k F [ i − 1 , k ] − P i ∗ k
当 j j j j − L i j-L_{i} j − L i
需要查询最优决策时, 队头即为所求。
有一个新的决策要加入候选集合时, 在队尾检查 F [ i − 1 , k ] − P i ∗ k F[i-1, k]-P_{i} * k F [ i − 1 , k ] − P i ∗ k
在本题中具体来说, 当内层循环开始时 ( j = S i ) \left(j=S_{i}\right) ( j = S i ) [ max ( S i − L i , 0 ) , S i − 1 ] \left[\max \left(S_{i}-L_{i}, 0\right), S_{i}-1\right] [ max ( S i − L i , 0 ) , S i − 1 ] ) ) ) j = S i ∼ N j=S_{i} \sim N j = S i ∼ N
因为每个决策至多入队、出队一次, 故转移的时间复杂度均推 O ( 1 ) O(1) O ( 1 ) O ( N M ) O(N M) O ( NM )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 struct rec {int L, P, S; } a[110 ];int n, m;int f[110 ][16010 ], q[16010 ];bool operator <(rec a, rec b) { return a.S < b.S; } int calc (int i, int k) return f[i - 1 ][k] - a[i].P * k; } int main () cin >> n >> m; for (int i = 1 ; i <= m; i++) scanf ("%d%d%d" , &a[i].L, &a[i].P, &a[i].S); sort (a + 1 , a + m + 1 ); for (int i = 1 ; i <= m; i++) { int l = 1 , r = 0 ; for (int k = max (0 , a[i].S - a[i].L); k <= a[i].S - 1 ; k++) { while (l <= r && calc (i, q[r]) <= calc (i, k)) r--; q[++r] = k; } for (int j = 1 ; j <= n; j++) { f[i][j] = max (f[i - 1 ][j], f[i][j - 1 ]); if (j >= a[i].S) { while (l <= r && q[l] < j - a[i].L) l++; if (l <= r) f[i][j] = max (f[i][j], calc (i, q[l]) + a[i].P * j); } } } cout << f[m][n] << endl; }
Solution
题目描述
给定一个长度为 N N N A A A M M M
试计算这个最小值。
输入格式
第一行包含两个整数 N N N M M M
第二行包含 N N N A A A
输出格式
输出一个整数,表示结果。
如果结果不存在,则输出 − 1 -1 − 1
数据范围
0 ≤ N ≤ 1 0 5 0 \le N \le 10^5 0 ≤ N ≤ 1 0 5 0 ≤ M ≤ 1 0 11 0 \le M \le 10^{11} 0 ≤ M ≤ 1 0 11 1 0 6 10^6 1 0 6
输入样例 :
输出样例 :
算法分析
设 F [ i ] F[i] F [ i ] i i i M M M
F [ i ] = min 0 ≤ j < i 并且 ∑ k = j + 1 i A k ≤ M { F [ j ] + max j + 1 ≤ k ≤ i { A k } } F[i]=\min _{0 \leq j<i \text { 并且 } \sum_{k=j+1}^{i} A_{k} \leq M}\left\{F[j]+\max _{j+1 \leq k \leq i}\left\{A_{k}\right\}\right\}
F [ i ] = 0 ≤ j < i 并且 ∑ k = j + 1 i A k ≤ M min { F [ j ] + j + 1 ≤ k ≤ i max { A k } }
若采用枚举决策 j j j O ( N ˙ 2 ) \mathrm{O}\left(\dot{N}^{2}\right) O ( N ˙ 2 ) max j + 1 ≤ k ≤ i { A k } \max _{j+1 \leq k \leq i}\left\{A_{k}\right\} max j + 1 ≤ k ≤ i { A k } j j j
引理:
在上述方程中, 若 j ( 0 ≤ j < i ) j(0 \leq j<i) j ( 0 ≤ j < i ) ∑ k = j + 1 i A k ≤ M \sum_{k=j+1}^{i} A_{k} \leq M ∑ k = j + 1 i A k ≤ M
A j = max j ≤ k ≤ i { A k } A_{j}=\max _{j \leq k \leq i}\left\{A_{k}\right\} A j = max j ≤ k ≤ i { A k } ∑ k = j i A k > M \sum_{k=j}^{i} A_{k}>M ∑ k = j i A k > M j j j ∑ k = j + 1 i A k ≤ M \sum_{k=j+1}^{i} A_{k} \leq M ∑ k = j + 1 i A k ≤ M j j j
证明:
反证法。假设两个条件都不满足, 即 A j < max j ≤ k ≤ i { A k } A_{j}<\max _{j \leq k \leq i}\left\{A_{k}\right\} A j < max j ≤ k ≤ i { A k } ∑ k = j i A k ≤ M \sum_{k=j}^{i} A_{k} \leq M ∑ k = j i A k ≤ M max j ≤ k ≤ i { A k } = max j + 1 ≤ k ≤ i { A k } \max _{j \leq k \leq i}\left\{A_{k}\right\}=\max _{j+1 \leq k \leq i}\left\{A_{k}\right\} max j ≤ k ≤ i { A k } = max j + 1 ≤ k ≤ i { A k } F F F F [ j − 1 ] ≤ F[j-1] \leq F [ j − 1 ] ≤ F [ j ] F[j] F [ j ]
F [ j − 1 ] + max j ≤ k ≤ i { A k } ≤ F [ j ] + max j + 1 ≤ k ≤ i { A k } F[j-1]+\max _{j \leq k \leq i}\left\{A_{k}\right\} \leq F[j]+\max _{j+1 \leq k \leq i}\left\{A_{k}\right\}
F [ j − 1 ] + j ≤ k ≤ i max { A k } ≤ F [ j ] + j + 1 ≤ k ≤ i max { A k }
上式的含义就是决策 j − 1 j-1 j − 1 j j j 0 ≤ j < i , j − 1 0 \leq j<i, j-1 0 ≤ j < i , j − 1 j j j j j j
引理中的第 2 个条件比较简单, 只需预处理出对于每个 i i i ∑ k = j + 1 i A k ≤ M \sum_{k=j+1}^{i} A_{k} \leq M ∑ k = j + 1 i A k ≤ M j j j C [ i ] C[i] C [ i ] F [ i ] F[i] F [ i ] C [ i ] C[i] C [ i ] j j j
根据引理, 当一个新的决策 j 2 j_{2} j 2 j 1 j_{1} j 1 j 1 < j 2 j_{1}<j_{2} j 1 < j 2 A j 1 ≤ A j 2 A_{j_{1}} \leq A_{j_{2}} A j 1 ≤ A j 2 j 1 j_{1} j 1
综上所述, 我们可以维护一个决策点 j j j A j A_{j} A j 的队列, 只有该队列中的元素才可能成为最优决策。
与上一道题目不同的是, 该队列只是一个 A j A_{j} A j F [ j ] + max j + 1 ≤ k ≤ i { A k } F[j]+\max _{j+1 \leq k \leq i}\left\{A_{k}\right\} F [ j ] + max j + 1 ≤ k ≤ i { A k } 0 × 71 0 \times 71 0 × 71 A j A_{j} A j F [ j ] + max j + 1 ≤ k s i { A k } F[j]+\max _{j+1 \leq k s i}\left\{A_{k}\right\} F [ j ] + max j + 1 ≤ k s i { A k }
最后, 关于 max j + 1 ≤ k ≤ i { A k } \max _{j+1 \leq k \leq i}\left\{A_{k}\right\} max j + 1 ≤ k ≤ i { A k } S T \mathrm{ST} ST O ( 1 ) O(1) O ( 1 ) max j + 1 s k s i { A k } \max _{j+1 s k s i}\left\{A_{k}\right\} max j + 1 s k s i { A k } A A A
在整个算法中, 每个 j j j O ( N log N ) O(N \log N) O ( N log N )
Solution
题目描述
有 N N N V V V
第 i i i s i s_i s i v i v_i v i w i w_i w i
求解将哪些物品装入背包,可使物品体积总和不超过背包容量,且价值总和最大。
输入格式
第一行两个整数,N , V N,V N , V ( 0 < N ≤ 1000 (0 \lt N \le 1000 ( 0 < N ≤ 1000 0 < V ≤ 20000 ) 0 \lt V \le 20000) 0 < V ≤ 20000 )
接下来有 N N N v i , w i , s i v_i, w_i, s_i v i , w i , s i i i i
输出格式
输出一个整数,表示最大价值。
数据范围
0 < N ≤ 1000 0 \lt N \le 1000 0 < N ≤ 1000 0 < V ≤ 20000 0 \lt V \le 20000 0 < V ≤ 20000 0 < v i , w i , s i ≤ 20000 0 \lt v_i, w_i, s_i \le 20000 0 < v i , w i , s i ≤ 20000
提示
本题考查多重背包的单调队列优化方法。
输入样例
1 2 3 4 5 4 5 1 2 3 2 4 1 3 4 3 4 5 2
输出样例 :
算法分析
我们已经介绍了多重背包问题的朴素解法和二进制拆分解法。若使用单调队列, 可以把求解多重背包问题的复杂度进一步优化到 O ( N M ) O(N M) O ( NM )
在背包的朴素解法中, DP 数组省略了 “阶段” 这一维。当外层循环进行到 i i i F [ j ] F[j] F [ j ] i i i j j j j j j i i i c n t c n t c n t
F [ j ] = max 1 ≤ c n t ≤ c l { F [ j − c n t ∗ V i ] + c n t ∗ W i } F[j]=\max _{1 \leq c n t \leq c_{l}}\left\{F\left[j-c n t * V_{i}\right]+c n t * W_{i}\right\}
F [ j ] = 1 ≤ c n t ≤ c l max { F [ j − c n t ∗ V i ] + c n t ∗ W i }
画出能够转移到状态 j j j { j − c n t ∗ V i ∣ 1 ≤ c n t ≤ C i } \left\{j-c n t * V_{i} \mid 1 \leq c n t \leq C_{i}\right\} { j − c n t ∗ V i ∣ 1 ≤ c n t ≤ C i }
当循环变量 j j j 1 1 1
可以发现, 相邻两个状态 j j j j − 1 j-1 j − 1 j − 1 j-1 j − 1 j j j
但是, 我们试着考虑一下状态 j j j j − V i j-V_{i} j − V i
这两者对应的决策候选集合之间的关系, 与我们前面讲解的单调队列题目非常相似, 只有一个新决策加入候选集合、一个已有决策被排除。所以,我们应该把状态 j j j V i V_{i} V i i i i
余数为 0 ⟼ 0 , V i , 2 V i , ⋯ 0 \longmapsto 0, V_{i}, 2 V_{i}, \cdots 0 ⟼ 0 , V i , 2 V i , ⋯
余数为 1 ⟼ 1 , 1 + V i , 1 + 2 V i , ⋯ 1 \longmapsto1 ,1+V_{i}, 1+2 V_{i}, \cdots 1 ⟼ 1 , 1 + V i , 1 + 2 V i , ⋯
⋯ \cdots ⋯
余数为 V i − 1 ⟼ ( V i − 1 ) , ( V i − 1 ) + V i , ( V i − 1 ) + 2 V i , ⋯ V_{i} - 1 \longmapsto \left(V_{i}-1\right),\left(V_{i}-1\right)+V_{i},\left(V_{i}-1\right)+2 V_{i}, \cdots V i − 1 ⟼ ( V i − 1 ) , ( V i − 1 ) + V i , ( V i − 1 ) + 2 V i , ⋯
把 “倒序循环 j j j u ∈ [ 0 , V i − 1 ] u \in\left[0, V_{i}-1\right] u ∈ [ 0 , V i − 1 ] p = ⌊ ( M − p=\lfloor(M- p = ⌊( M − u ) / V i ⌋ ∼ 0 \left.u) / V_{i}\right\rfloor \sim 0 u ) / V i ⌋ ∼ 0 j = u + p ∗ V i j=u+p * V_{i} j = u + p ∗ V i i i i C i C_{i} C i j = j= j = u + p ∗ V i u+p * V_{i} u + p ∗ V i { u + k ∗ V i ∣ p − C i ≤ k ≤ p − 1 } \left\{u+k * V_{i} \mid p-C_{i} \leq k \leq p-1\right\} { u + k ∗ V i ∣ p − C i ≤ k ≤ p − 1 }
F [ u + p ∗ V i ] = max p − C i ≤ k ≤ p − 1 { F [ u + k ∗ V i ] + ( p − k ) ∗ W i } F\left[u+p * V_{i}\right]=\max _{p-C_{i} \leq k \leq p-1}\left\{F\left[u+k * V_{i}\right]+(p-k) * W_{i}\right\}
F [ u + p ∗ V i ] = p − C i ≤ k ≤ p − 1 max { F [ u + k ∗ V i ] + ( p − k ) ∗ W i }
k k k f f f i i i k = p k=p k = p
与本节的 “ Fence"一题类似, 把外层循环 i i i u u u p p p k k k [ p − C i , p − 1 ] \left[p-C_{i}, p-1\right] [ p − C i , p − 1 ] p p p p ∗ W i p * W_{i} p ∗ W i k k k F [ u + k ∗ V i ] − k ∗ W i F\left[u+k * V_{i}\right]-k * W_{i} F [ u + k ∗ V i ] − k ∗ W i k k k F [ u + k ∗ V i ] − k ∗ W i F[u+ \left.k * V_{i}\right]-k * W_{i} F [ u + k ∗ V i ] − k ∗ W i p p p
检查队头合法性, 把大于 p − 1 p-1 p − 1
取队头为最优决策, 更新 F [ u + p ∗ V i ] F\left[u+p * V_{i}\right] F [ u + p ∗ V i ]
把新决策 k = p − C i − 1 k=p-C_{i}-1 k = p − C i − 1
整个算法的时间复杂度为 O ( N M ) \mathrm{O}(N M) O ( NM )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 int calc (int i, int u, int k) return f[u + k*V[i]] - k*W[i]; } int main () cin >> n >> m; memset (f, 0xcf , sizeof f[0 ] = 0 ; for (int i = 1 ; i <= n; i++) { scanf ("%d%d%d" , &V[i], &W[i], &C[i]); for (int u = 0 ; u < V[i]; u++) { int l = 1 , r = 0 ; int maxp = (m - u) / V[i]; for (int k = maxp - 1 ; k >= max (maxp - C[i], 0 ); k--) { while (l <= r && calc (i, u, q[r]) <= calc (i, u, k)) r--; q[++r] = k; } for (int p = maxp; p >= 0 ; p--) { while (l <= r && q[l] > p - 1 ) l++; if (l <= r) f[u + p*V[i]] = max (f[u + p*V[i]], calc (i, u, q[l]) + p*W[i]); if (p - C[i] - 1 >= 0 ) { while (l <= r && calc (i, u, q[r]) <= calc (i, u, p - C[i] - 1 )) r--; q[++r] = p - C[i] - 1 ; } } } } int ans = 0 ; for (int i = 1 ; i <= m; i++) ans = max (ans, f[i]); cout << ans << endl; }
单调队列优化 DP 模型总结
最后, 我们对单调队列优化 DP 的模型进行总结。我们重新写出上面三道例题的状态转移方程:
题目
状态转移方程
定值(外层循环)
状态变量(内层循环)
决策变量
最大子序列和
a n s = max 1 ≤ i ≤ N { S [ i ] − min i − M ≤ j ≤ i − 1 { S [ j ] } } a n s=\max _{1 \leq i \leq N}\left\{S[i]-\min _{i-M \leq j \leq i-1}\{S[j]\}\right\} an s = max 1 ≤ i ≤ N { S [ i ] − min i − M ≤ j ≤ i − 1 { S [ j ]} } i i i j j j
围栏
F [ i , j ] = max j − L i ≤ k ≤ S i − 1 { F [ i − 1 , k ] + P i ∗ ( j − k ) } , 其中 j ≥ S i F[i, j]=\max _{j-L_{i} \leq k \leq S_{i}-1}\left\{F[i-1, k]+P_{i} *(j-k)\right\} \text {, 其中 } j \geq S_{i} F [ i , j ] = max j − L i ≤ k ≤ S i − 1 { F [ i − 1 , k ] + P i ∗ ( j − k ) } , 其中 j ≥ S i i i i j j j k k k
裁剪序列
F [ i ] = min 0 ≤ j < i 并且 ∑ k = j + 1 i A k ≤ M { F [ j ] + max j + 1 ≤ k ≤ i { A k } } F[i]=\min _{0 \leq j<i \text { 并且 } \sum_{k=j+1}^{i} A_{k} \leq M}\left\{F[j]+\max _{j+1 \leq k \leq i}\left\{A_{k}\right\}\right\} F [ i ] = min 0 ≤ j < i 并且 ∑ k = j + 1 i A k ≤ M { F [ j ] + max j + 1 ≤ k ≤ i { A k } } i i i j j j
多重背包
F [ u + p ∗ V i ] = max p − C i ≤ k ≤ p − 1 { F [ u + k ∗ V i ] + ( p − k ) ∗ W i } F\left[u+p * V_{i}\right]=\max _{p-C_{i} \leq k \leq p-1}\left\{F\left[u+k * V_{i}\right]+(p-k) * W_{i}\right\} F [ u + p ∗ V i ] = max p − C i ≤ k ≤ p − 1 { F [ u + k ∗ V i ] + ( p − k ) ∗ W i } i , u i,u i , u p p p k k k
只关注 “状态变量” “决策变量” 及其所在的维度, 这些状态转移方程都可以大致归为如下形式 (除第三个方程稍有不同):
F [ i ] = min L ( i ) ≤ j ≤ R ( i ) { F [ j ] + val ( i , j ) } F[i]=\min _{L(i) \leq j \leq R(i)}\{F[j]+\operatorname{val}(i, j)\}
F [ i ] = L ( i ) ≤ j ≤ R ( i ) min { F [ j ] + val ( i , j )}
上式所代表的问题覆盖范围广泛, 是 DP 中一类非常基本、非常重要的模型。这种模型也被称为 1D/1D 的动态规划 。它是一个最优化问题, L ( i ) L(i) L ( i ) R ( i ) R(i) R ( i ) i i i j j j v a l ( i , j ) val (i, j) v a l ( i , j ) i i i j j j
回想前面三道例题的解法, 我们都把 v a l ( i , j ) v a l(i, j) v a l ( i , j ) i i i j j j i i i j j j F [ i ] F[i] F [ i ] i i i i i i 在上述模型中, 多项式 v a l ( i , j ) val (i, j) v a l ( i , j ) i i i j j j 。
题目描述
输入一个长度为 n n n m m m
注意: 子序列的长度至少是 1 1 1
输入格式
第一行输入两个整数 n , m n,m n , m
第二行输入 n n n n n n
同一行数之间用空格隔开。
输出格式
输出一个整数,代表该序列的最大子序和。
数据范围
1 ≤ n , m ≤ 300000 1 \le n,m \le 300000 1 ≤ n , m ≤ 300000
输入样例 :
输出样例 :
算法分析
计算 “区间和” 的问题, 一般转化为 “两个前缀和相减” 的形式进行求解。我们先求出 S [ i ] S[i] S [ i ] i i i [ L , R ] [L, R] [ L , R ] S [ R ] − S[R]- S [ R ] − S [ L − 1 ] S[L-1] S [ L − 1 ] x , y x, y x , y S [ y ] − S [ x ] S[y]-S[x] S [ y ] − S [ x ] y − x ≤ M y- x \leq M y − x ≤ M
首先我们枚举右端点 i i i i i i 找到一个左端点 j j j j ∈ [ i − m , i − 1 ] j \in[i-m, i-1] j ∈ [ i − m , i − 1 ] S [ j ] S[j] S [ j ] 。
不妨比较一下任意两个位置 j j j k k k k < j < i k<j<i k < j < i S [ k ] ≥ S [ j ] S[k] \geq S[j] S [ k ] ≥ S [ j ] i i i k k k S [ k ] S[k] S [ k ] S [ j ] S[j] S [ j ] j j j i i i M M M j j j k k k j j j k k k
以上比较告诉我们, 可能成为最优选择的策略集合一定是一个 “下标位置递增、对应的前缀和 S S S ” 的序列。我们可以用一个队列保存这个序列。随着右端点变从前向后扫描, 我们对每个 i i i
判断队头决策与 i i i M M M
此时队头就是右端点为 i i i j j j
不断删除队尾决策, 直到队尾对应的 S S S S [ i ] S[i] S [ i ] i i i
1 2 3 4 5 6 7 8 int l = 1 , r = 1 ;q[1 ] = 0 ; for (int i = 1 ; i <= n; i++) { while (l <= r && q[l] < i - m) l++; ans = max (ans, sum[i] - sum[q[l]]); while (l <= r && sum[q[r]] >= sum[i]) r--; q[++r] = i; }
这就是著名的单调队列算法, 因为每个元素至多入队一次、出队一次, 所以整个算法的时间复杂度为 O ( N ) O(N) O ( N )
Solution
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 #include <iostream> using namespace std;const int N = 300010 , INF = 0x3f3f3f3f ;int n, m;int s[N], q[N], hh = 0 , tt = -1 ;int main () cin >> n >> m; for (int i = 1 ; i <= n; ++i) { cin >> s[i]; s[i] += s[i - 1 ]; } int maxv = -INF; q[++tt] = 0 ; for (int i = 1 ; i <= n; ++i) { if (hh <= tt && q[hh] < i - m) ++hh; maxv = max (maxv, s[i] - s[q[hh]]); while (hh <= tt && s[i] <= s[q[tt]]) --tt; q[++tt] = i; } cout << maxv; }
题目描述
在一年前赢得了小镇的最佳草坪比赛后,FJ 变得很懒,再也没有修剪过草坪。
现在,新一轮的最佳草坪比赛又开始了,FJ 希望能够再次夺冠。
然而,FJ 的草坪非常脏乱,因此,FJ 只能够让他的奶牛来完成这项工作。
FJ 有 N N N 1 1 1 N N N
每只奶牛的效率是不同的,奶牛 i i i E i E_i E i
编号相邻的奶牛们很熟悉,如果 FJ 安排超过 K K K
因此,现在 FJ 需要你的帮助,找到最合理的安排方案并计算 FJ 可以得到的最大效率。
注意,方案需满足不能包含超过 K K K
输入格式
第一行:空格隔开的两个整数 N N N K K K
第二到 N + 1 N+1 N + 1 i + 1 i+1 i + 1 E i E_i E i
输出格式
共一行,包含一个数值,表示 FJ 可以得到的最大的效率值。
数据范围
1 ≤ N ≤ 1 0 5 1 \le N \le 10^5 1 ≤ N ≤ 1 0 5 0 ≤ E i ≤ 1 0 9 0 \le E_i \le 10^9 0 ≤ E i ≤ 1 0 9
输入样例 :
输出样例 :
样例解释
FJ 有 5 只奶牛,效率分别为 1、2、3、4、5。
FJ 希望选取的奶牛效率总和最大,但是他不能选取超过 2 只连续的奶牛。
因此可以选择第三只以外的其他奶牛,总的效率为 1 + 2 + 4 + 5 = 12。
算法分析
这里提供一个转化的思路,题目要求最多连续选k个使效率最大 每k + 1个里必须不选 1 个 ,使不选的总效率最小,最后用总效率减去不选的效率即可
f[i] 表示不选第 i 个的最小不选效率,从前k + 1个里转移即可,可以参考 烽火传递 这道题
Solution
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 #include <iostream> using namespace std;const int N = 1e5 + 10 ;int n, k;long long f[N], w[N];int q[N], hh = 0 , tt = -1 ;int main () cin >> n >> k; long long sum = 0 ; for (int i = 1 ; i <= n; ++i) cin >> w[i], sum += w[i]; q[++tt] = 0 ; for (int i = 1 ; i <= n; ++i) { if (hh <= tt && q[hh] < i - k - 1 ) ++hh; f[i] = f[q[hh]] + w[i]; while (hh <= tt && f[q[tt]] >= f[i]) --tt; q[++tt] = i; } long long minv = 9e18 ; for (int i = n - k; i <= n; ++i) minv = min (minv, f[i]); cout << sum - minv; }
题目描述
John 打算驾驶一辆汽车周游一个环形公路。
公路上总共有 n n n
John 必须从某个车站出发,一直按顺时针(或逆时针)方向走遍所有的车站,并回到起点。
在一开始的时候,汽车内油量为零,John 每到一个车站就把该站所有的油都带上(起点站亦是如此),行驶过程中不能出现没有油的情况。
任务:判断以每个车站为起点能否按条件成功周游一周。
输入格式
第一行是一个整数 n n n
接下来 n n n p i , d i p_i,d_i p i , d i i i i i i i 顺时针方向 下一站的距离。
输出格式
输出共 n n n i i i i i i
数据范围
3 ≤ n ≤ 1 0 6 3 \le n \le 10^6 3 ≤ n ≤ 1 0 6 0 ≤ p i ≤ 2 × 1 0 9 0 \le p_i \le 2 \times 10^9 0 ≤ p i ≤ 2 × 1 0 9 0 ≤ d i ≤ 2 × 1 0 9 0 \le d_i \le 2 \times 10^9 0 ≤ d i ≤ 2 × 1 0 9
输入样例 :
输出样例 :
算法分析
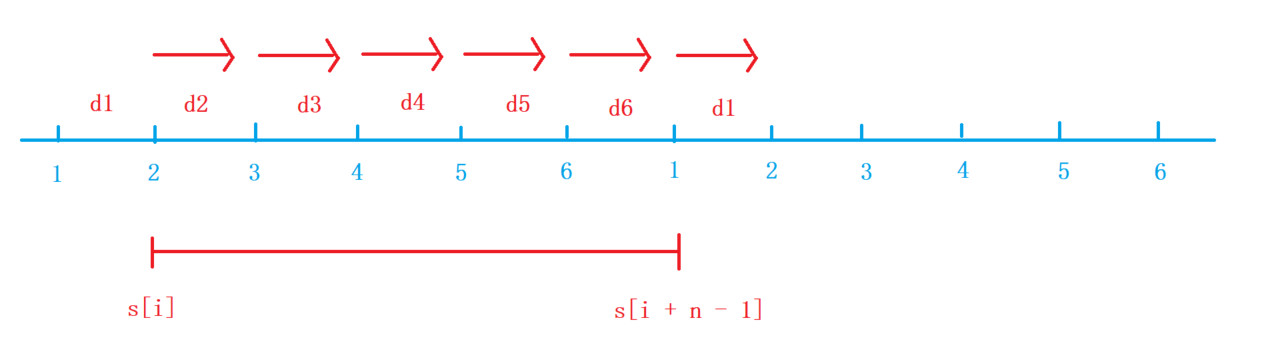
顺时针
i表示从i点加oil[i]的油再耗dist[i]的油所剩的油量,即oil[i] - dist[i]
1、计算出油量的前缀和
2、从某个点i出发,顺时针走一圈,在过程中油量始终 >= 0,等价于在[i,i + n - 1]中,对任意的j,i <= j <= i + n - 1,均有s[j] - s[i - 1] >= 0,即i固定,找s[j]的最小值,即从[i,i + n - 1]中找到滑动窗口的最小值
3、由于2操作,需要对i进行反向遍历,即从n * 2遍历到1,又由于i <= j <= i + n - 1,遍历到i时需要用到i位置的值,因此找[i,i + n - 1]区间最小值时需要在while后面的语句找
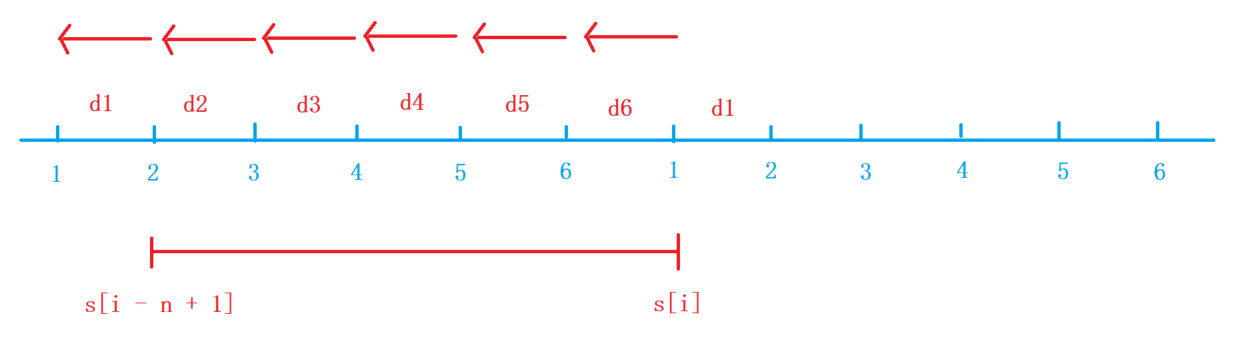
逆时针
i表示从i点加oil[i]的油再耗dist[i - 1]的油所剩的油量,即oil[i] - dist[i - 1],其中1号点浩的是dist[n]的油,因此需要初始化dist[0] = dist[n]
1、计算出油量的后缀和
2、从某个点i出发,逆时针走一圈,在过程中油量始终 >= 0,等价于在[i - n + 1,i]中,对任意的j,i - n + 1 <= j <= i,均有s[j] - s[i + 1] >= 0,即i固定,找s[j]的最小值,即从[i - n + 1,i]中找到滑动窗口的最小值
3、由于2操作,需要对i进行正向遍历,即从1遍历到n * 2,又由于i - n + 1 <= j <= i,遍历到i时需要用到i位置的值,因此找[i - n + 1,i]区间最小值时需要在while后面的语句找
Solution
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 #include <iostream> #include <cstring> #include <algorithm> using namespace std;const int N = 1e6 + 10 ;int n;int p[N], d[N];long long s[N];int q[N], hh = 0 , tt = -1 ;bool ans[N];int main () cin >> n; for (int i = 1 ; i <= n; ++i) { cin >> p[i] >> d[i]; s[i] = s[i + n] = p[i] - d[i]; } for (int i = 1 ; i <= 2 * n; ++i) s[i] += s[i - 1 ]; for (int i = 2 * n; i; --i) { if (hh <= tt && q[hh] >= i + n) ++hh; while (hh <= tt && s[q[tt]] >= s[i]) --tt; q[++tt] = i; if (i <= n && s[q[hh]] - s[i - 1 ] >= 0 ) ans[i] = true ; } d[0 ] = d[n]; for (int i = 1 ; i <= n; ++i) s[i] = s[i + n] = p[i] - d[i - 1 ]; for (int i = 2 * n; i; --i) s[i] += s[i + 1 ]; hh = 0 , tt = -1 ; for (int i = 1 ; i <= 2 * n; ++i) { if (hh <= tt && q[hh] <= i - n) ++hh; while (hh <= tt && s[q[tt]] >= s[i]) --tt; q[++tt] = i; if (i > n && s[q[hh]] - s[i + 1 ] >= 0 ) ans[i - n] = true ; } for (int i = 1 ; i <= n; ++i) { if (ans[i]) cout << "TAK" << endl; else cout << "NIE" << endl; } }
题目描述
烽火台是重要的军事防御设施,一般建在交通要道或险要处。
一旦有军情发生,则白天用浓烟,晚上有火光传递军情。
在某两个城市之间有 n n n
为了使情报准确传递,在连续 m m m
现在输入 n , m n,m n , m
输入格式
第一行是两个整数 n , m n,m n , m
第二行 n n n a i a_i a i
输出格式
输出仅一个整数,表示最小代价。
数据范围
1 ≤ n , m ≤ 2 × 1 0 5 1 \le n,m \le 2 \times 10^5 1 ≤ n , m ≤ 2 × 1 0 5 0 ≤ a i ≤ 1000 0 \le a_i \le 1000 0 ≤ a i ≤ 1000
输入样例 :
输出样例 :
算法分析
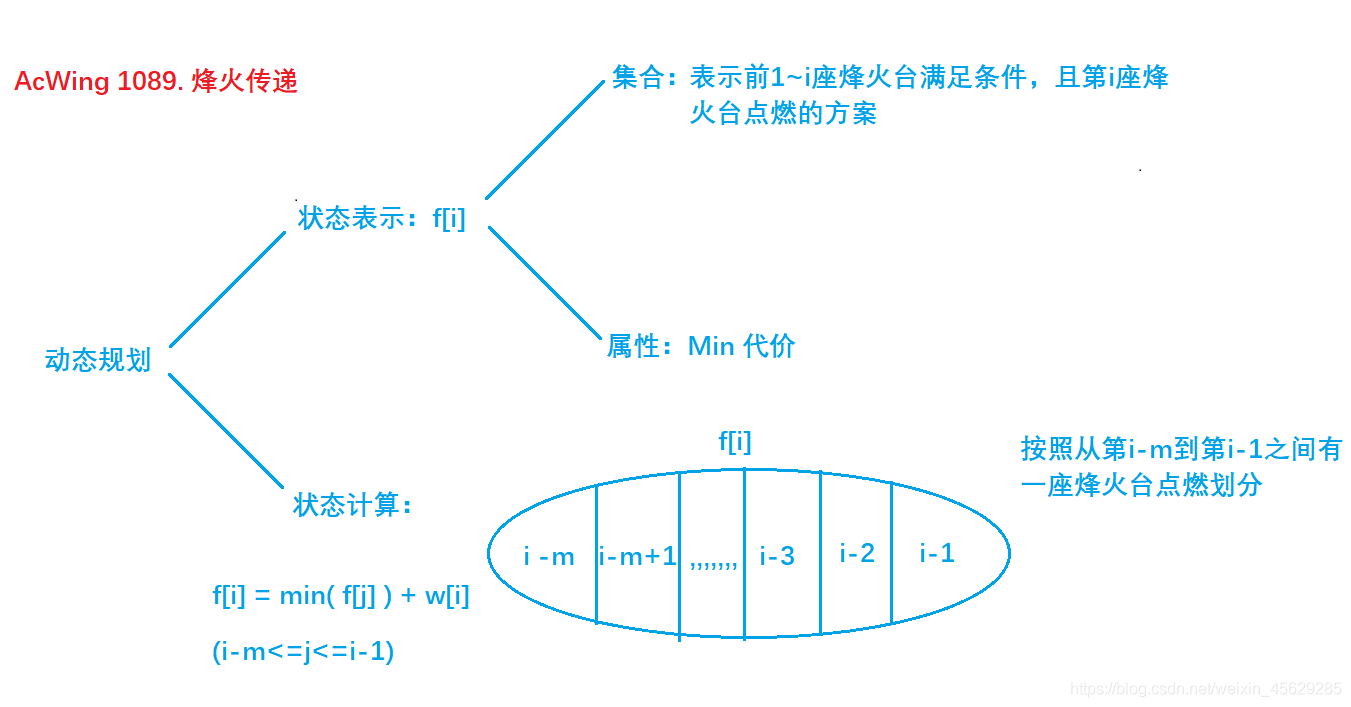
状态表示: f[i]表示前1~i座烽火台满足条件,且第i座烽火台点燃的方案集合。属性: 所有符合条件的方案集合中的最小代价值。
状态计算:
如何划分集合?
题目要求在连续 m个烽火台中至少要有一个发出信号,即连续的m个烽火台中至少要有一个被点燃。而f[i]表示的含义中,第i座已经被点燃,因此在第i座向前的前m座烽火台至少要有一个被点燃。被点燃的可以是第 i-m, 第 i-m+1, ⋯ \cdots ⋯ i-3,第i-2,第i-1座。
故状态计算方程: f[i] = min(f[j]) + w[i] (i-m<=j<=i-1)
一段区间的最值可以用单调队列求解。此题中,我们定义一个单调递增队列,队列中维护的是f[j]集合。每次拿出队头元素,即长为m的区间中,值最小的f[j]来更新答案。
其实有个小疑问 ,为什么状态表示时,要将第i座表示为点燃?
我们可以从问题出发,每n座烽火台中必然要有一座要被点燃。那么最后n座烽火台同样也是如此。如果我们将f[i]定义为前1~i座烽火台满足条件,且第i座烽火台点燃的方案集合。那么答案一定在 f[n-m+1],f[n-m+2],,,f[n]之间。也就是说将第i座表示为点燃可以很容易表示出答案。这就给我们一个启发,我们在定义状态表示时,一定要考虑我们定义的状态是否可以包含答案 。
最后可以暴力枚举 最终状态 f[i],其中 n − m + 1 ≤ i ≤ n n - m + 1 \le i \le n n − m + 1 ≤ i ≤ n
这里可以巧妙利用我们的 滑动窗口
首先我们知道,单调队列 维护的是 i − m ≤ j ≤ i − 1 i - m \le j \le i - 1 i − m ≤ j ≤ i − 1 f j f_j f j
循环迭代完第 n n n j j j n − m ≤ j ≤ n n - m \le j \le n n − m ≤ j ≤ n
f [ n ] f[n] f [ n ] n + 1 n+1 n + 1
所以结束的时候,把滑动窗口往后多划一位,把 j j j n − m + 1 ≤ j ≤ n n - m + 1 \le j \le n n − m + 1 ≤ j ≤ n
则 单调队列 的 队头元素 ,就是该范围内的 值最小的最终状态 ,输出 队头元素 即可
Solution
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 #include <iostream> using namespace std;const int N = 2e5 + 10 ;int n, m;int f[N], a[N];int q[N], hh = 0 , tt = -1 ;int main () cin >> n >> m; for (int i = 1 ; i <= n; ++i) cin >> a[i]; q[++tt] = 0 ; for (int i = 1 ; i <= n; ++i) { if (hh <= tt && q[hh] < i - m) ++hh; f[i] = f[q[hh]] + a[i]; while (hh <= tt && f[q[tt]] >= f[i]) --tt; q[++tt] = i; } int ans = 1e9 ; for (int i = n; i >= n - m + 1 ; --i) ans = min (ans, f[i]); if (hh <= tt && q[hh] < n - m + 1 ) ++hh; cout << f[q[hh]]; }
题目描述
高二数学《绿色通道》总共有 n n n 1 , 2 , … , n 1,2,…,n 1 , 2 , … , n i i i a i a_i a i
小 Y 决定只用不超过 t t t
每道题要么不写,要么抄完,不能写一半。
下标连续的一些空题称为一个空题段,它的长度就是所包含的题目数。
这样应付自然会引起马老师的愤怒,最长的空题段越长,马老师越生气。
现在,小 Y 想知道他在这 t t t
由于小 Y 很聪明,你只要告诉他最长的空题段至少有多长就可以了,不需输出方案。
输入格式
第一行为两个整数 n , t n,t n , t
第二行为 n n n a 1 , a 2 , … , a n a_1,a_2,…,a_n a 1 , a 2 , … , a n
输出格式
输出一个整数,表示最长的空题段至少有多长。
数据范围
0 < n ≤ 5 × 1 0 4 0 < n \le 5 \times 10^4 0 < n ≤ 5 × 1 0 4 0 < a i ≤ 3000 0 < a_i \le 3000 0 < a i ≤ 3000 0 < t ≤ 1 0 8 0 < t \le 10^8 0 < t ≤ 1 0 8
输入样例 :
1 2 17 11 6 4 5 2 5 3 4 5 2 3 4 5 2 3 6 3 5
输出样例 :
算法分析
本题相当于给定我们一个数组a,让我们选出一些数据,让选出的数据和不能超过t,在此前提下,那些没选的数会构成很多连续的段,我们要让这些段的最大值最小。
本题可以使用二分,使用二分的本质是答案具有两段性,假设答案是ans,因为ans是最小的一个,因此小于ans的空题段长度会导致用时超过题目给定的t;大于ans的空题段长度是满足条件的,这是因为允许空的题目长度更长了,用时一定更少了。
我们可以在[0, n]中枚举答案mid,每次检查最大空题段长度不大于mid是否满足题意即可,这样就转化为了1089. 烽火传递 。也就是说最多有连续的mid个数可以不被选。
Solution
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 #include <iostream> using namespace std;const int N = 5e4 + 10 ;int n, t;int f[N], a[N];int q[N], hh = 0 , tt = -1 ;bool check (int limit) hh = 0 , tt = -1 ; q[++tt] = 0 ; for (int i = 1 ; i <= n; ++i) { if (hh <= tt && q[hh] < i - limit - 1 ) ++hh; f[i] = f[q[hh]] + a[i]; while (hh <= tt && f[q[tt]] >= f[i]) --tt; q[++tt] = i; } int minv = 1e9 ; for (int i = n; i >= n - limit; --i) minv = min (minv, f[i]); return minv <= t; } int main () cin >> n >> t; for (int i = 1 ; i <= n; ++i) cin >> a[i]; int l = 0 , r = n; while (l < r) { int mid = l + r >> 1 ; if (check (mid)) r = mid; else l = mid + 1 ; } cout << l; }
题目描述
有一个 a × b a \times b a × b n × n n \times n n × n
输入格式
第一行为三个整数,分别表示 a , b , n a,b,n a , b , n
第二行至第 a + 1 a+1 a + 1 b b b
输出格式
输出仅一个整数,为 a × b a \times b a × b n × n n \times n n × n
数据范围
2 ≤ a , b ≤ 1000 2 \le a,b \le 1000 2 ≤ a , b ≤ 1000 n ≤ a , n ≤ b , n ≤ 100 n \le a,n \le b,n \le 100 n ≤ a , n ≤ b , n ≤ 100 1 0 9 10^9 1 0 9
输入样例 :
1 2 3 4 5 6 5 4 2 1 2 5 6 0 17 16 0 16 17 2 1 2 10 2 1 1 2 2 2
输出样例 :
算法分析
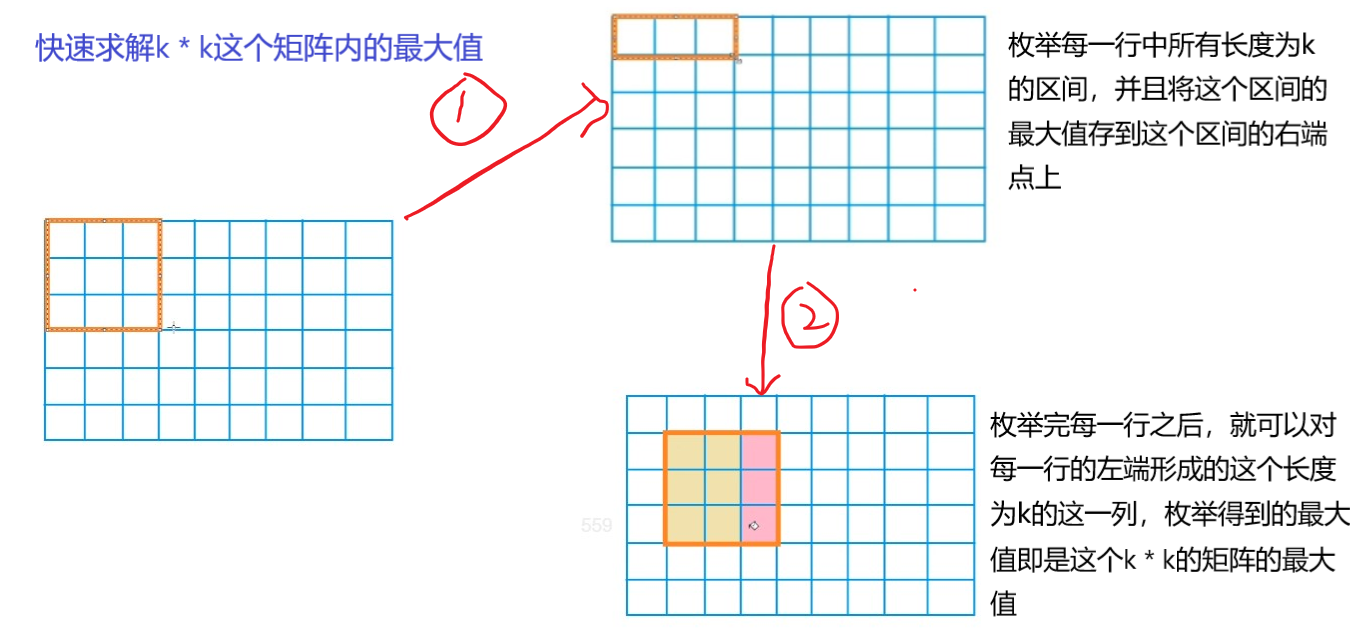
图中红色阴影格为该行中的最值元素,绿色背影色格为整个矩阵的最值元素。我们可以预处理出每列的行中最值,再对该列求一个最值,就是该子矩阵的最值。
Solution
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 #include <iostream> #include <cstring> #include <algorithm> using namespace std;const int N = 1010 ;int n, m, k;int w[N][N];int rowMax[N][N], rowMin[N][N];int colMax[N][N], colMin[N][N];int q[N], hh = 0 , tt = -1 ;void getMin (int w[], int rowMin[], int r) hh = 0 , tt = -1 ; for (int i = 1 ; i <= r; ++i) { if (hh <= tt && q[hh] <= i - k) ++hh; while (hh <= tt && w[q[tt]] >= w[i]) --tt; q[++tt] = i; rowMin[i] = w[q[hh]]; } } void getMax (int w[], int rowMax[], int r) hh = 0 , tt = -1 ; for (int i = 1 ; i <= r; ++i) { if (hh <= tt && q[hh] <= i - k) ++hh; while (hh <= tt && w[q[tt]] <= w[i]) --tt; q[++tt] = i; rowMax[i] = w[q[hh]]; } } int main () scanf ("%d%d%d" , &n, &m, &k); for (int i = 1 ; i <= n; ++i) for (int j = 1 ; j <= m; ++j) scanf ("%d" , &w[i][j]); for (int i = 1 ; i <= n; ++i) { getMin (w[i], rowMin[i], m); getMax (w[i], rowMax[i], m); } int tempMin[N], tempMax[N], ans = 1e9 ; for (int j = k; j <= m; ++j) { for (int i = 1 ; i <= n; ++i) { tempMin[i] = rowMin[i][j]; tempMax[i] = rowMax[i][j]; } getMin (tempMin, colMin[j], n); getMax (tempMax, colMax[j], n); for (int i = k; i <= n; ++i) ans = min (ans, colMax[j][i] - colMin[j][i]); } cout << ans; }