二叉树

二叉树遍历

二叉树前序遍历

递归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    vector<int> ans;
    vector<int> preorderTraversal(TreeNode* root) {
        dfs(root);
        return ans;
    }
  
    void dfs(TreeNode* root) {
        if (!root) return;
        ans.push_back(root->val);
        dfs(root->left);
        dfs(root->right);
    }
};

用栈模拟递归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> ans;
        if (!root) return ans;
        stack<TreeNode*> stk;
        stk.push(root);
        while (stk.size()) {
            auto now = stk.top(); stk.pop();
            ans.push_back(now->val);
            if (now->right) stk.push(now->right);
            if (now->left) stk.push(now->left);
        }
        return ans;
    }
};

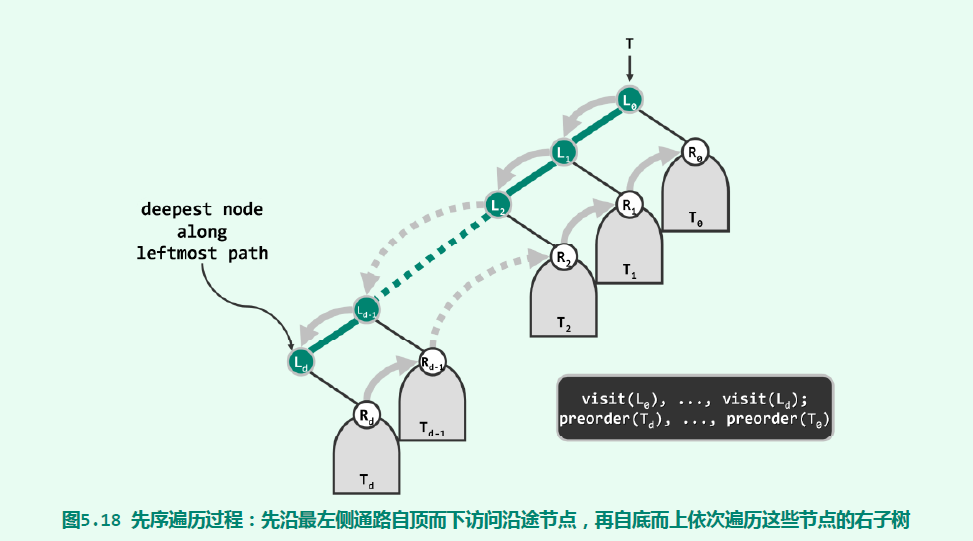
沿左分支自顶向下遍历沿途节点，再自顶向上遍历右子树

二叉树遍历-2021-12-29-18-46-02

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> ans;
        if (!root) return ans;
        stack<TreeNode*> stk;
        while (root || stk.size()) {
            while (root) {
                ans.push_back(root->val);
                stk.push(root);
                root = root->left;
            }
            root = stk.top()->right;
            stk.pop();
        }
        return ans;
    }
};

二叉树中序遍历

递归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    vector<int> ans;
    vector<int> inorderTraversal(TreeNode* root) {
        dfs(root);
        return ans;
    }
    void dfs(TreeNode *root) {
        if (!root) return;
        dfs(root->left);
        ans.push_back(root->val);
        dfs(root->right);
    }
};

用栈模拟递归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
public:
    vector<int> ans;
    stack<pair<TreeNode*, int>> stk;
    vector<int> inorderTraversal(TreeNode* root) {
        stk.push({root, 0});
        while (stk.size()) {
            if (stk.top().first == nullptr) {
                stk.pop();
                continue;
            }
            auto &t = stk.top().second;
            auto now = stk.top().first;
            if (t == 0) {
                stk.push({now->left, 0});
                t = 1;
            } else if (t == 1) {
                ans.push_back(now->val);
                stk.push({now->right, 0});
                t = 2;
            } else {
                stk.pop();
            }
        }
        return ans;
    }
};

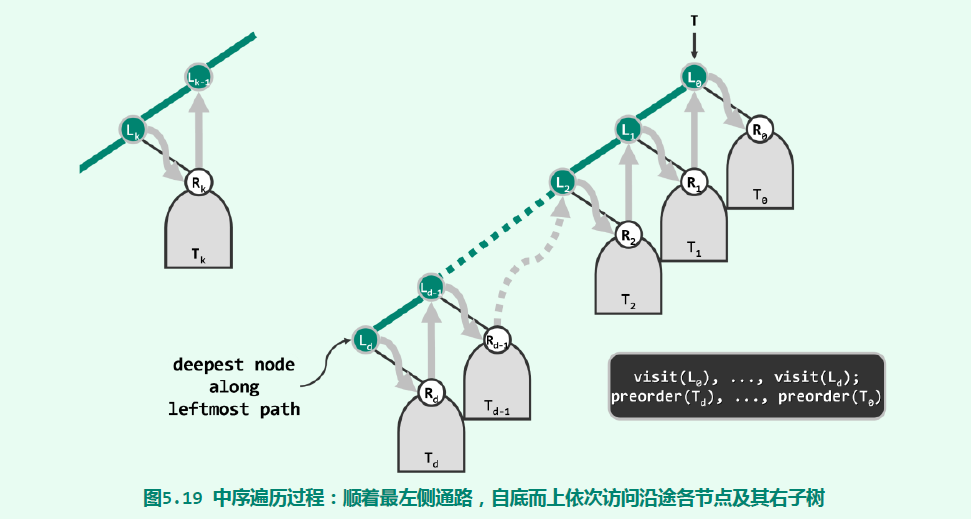
沿着最左侧通路，自底向上依次访问沿途节点及其右子树

二叉树遍历-2021-12-29-18-46-19

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    vector<int> ans;
    vector<int> inorderTraversal(TreeNode* root) {
        stack<TreeNode *> stk;
        while (root || stk.size()) {
            while (root) {
                stk.push(root);
                root = root->left;
            }
            root = stk.top(); stk.pop();
            ans.push_back(root->val);
            root = root->right;
        }
        return ans;
    }
};

二叉树后序遍历

递归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    vector<int> ans;
    vector<int> postorderTraversal(TreeNode* root) {
        dfs(root);
        return ans;
    }
    void dfs(TreeNode *root) {
        if (!root) return;
        dfs(root->left);
        dfs(root->right);
        ans.push_back(root->val);
    }
};

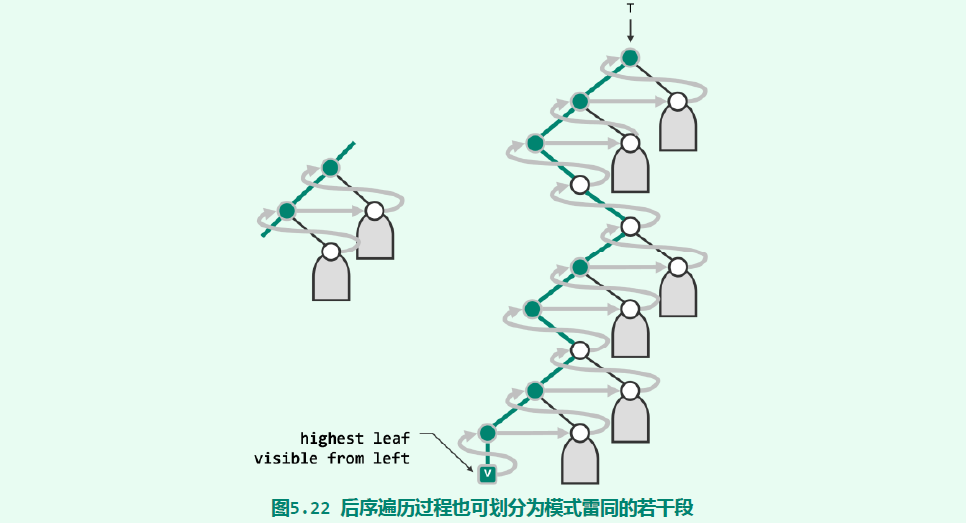
最高左侧可见叶节点（HLVFL）即为后序遍历首先访问的节点

二叉树遍历-2021-12-29-18-44-54

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> ans;
        if (!root) return ans;
        stack<TreeNode*> stk;
        stk.push(root);
        auto now = root;
        while (stk.size()) {
            auto nxt = stk.top();
            // 如果栈顶是当前节点的父节点，则必为当前节点的后序遍历后继节点
            // 反之，栈顶是当前节点的右兄弟，则是当前节点的后继子树，开始遍历右兄弟为根的子树
            if (now != nxt->left && now != nxt->right) {
 		// 当前节点的右兄弟存在，在以右兄弟为根的子树中，找到HLVFL(递归深入)
                while (nxt) {
                    if (nxt->left) {
                        if (nxt->right) stk.push(nxt->right);
                        stk.push(nxt->left);
                        nxt = nxt->left;
                    } else if (nxt->right) {
                        stk.push(nxt->right);
                        nxt = nxt->right;
                    } else break;
                }
		// 结束后栈顶 nxt 即是当前节点的后序遍历的后继节点
            } 
	    // now 更新为栈顶，即当前节点的后序遍历的后继节点
            now = nxt;
            stk.pop();
            ans.push_back(now->val);
        }
        return ans;
    }
};

先求（根,右,左），可使用沿右侧分支写法，再反转成（左,右,根）的后序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> ans;
        stack<TreeNode*> stk;
        while (root || stk.size()) {
            while (root) {
                ans.push_back(root->val);
                stk.push(root);
                root = root->right;
            }
            root = stk.top()->left;
            stk.pop();
        }
        reverse(ans.begin(), ans.end());
        return ans;
    }
};

链表头部插入

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        list<int> ans;
        stack<TreeNode*> stk;
        if (!root) return {ans.begin(), ans.end()};
        stk.push(root);
        while (stk.size()) {
            auto now = stk.top(); stk.pop();
            ans.push_front(now->val);
            if (now->left) stk.push(now->left);
            if (now->right) stk.push(now->right);
        }
        return {ans.begin(), ans.end()};
    }
};

二叉树层次遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> ans;
        queue<TreeNode*> q;
        if (root) q.push(root);

        while (q.size()) {
            vector<int> level;
            int len = q.size(); //记录当前层大小
            // 当前层有 len 个点，只需出队扩展 len 次
            while (len--) {
                auto t = q.front();
                q.pop();
                level.push_back(t->val);
                if (t->left) q.push(t->left);
                if (t->right) q.push(t->right);
            }

            ans.push_back(level);
        }
        return ans;
    }
};

二叉树生成

关键在于确定根节点

105. 从前序与中序遍历序列构造二叉树

给定一棵树的前序遍历 preorder 与中序遍历  inorder。请构造二叉树并返回其根节点。

示例 1:

1
2
Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
Output: [3,9,20,null,null,15,7]

示例 2:

1
2
Input: preorder = [-1], inorder = [-1]
Output: [-1]

提示:

  • 1 <= preorder.length <= 3000
  • inorder.length == preorder.length
  • -3000 <= preorder[i], inorder[i] <= 3000
  • preorder 和 inorder 均无重复元素
  • inorder 均出现在 preorder
  • preorder 保证为二叉树的前序遍历序列
  • inorder 保证为二叉树的中序遍历序列

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    unordered_map<int, int> pos;
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        int n = preorder.size();
        for (int i = 0; i < n; ++i) pos[inorder[i]] = i; 
        return build(preorder, inorder, 0, n - 1, 0, n - 1);
    }
    TreeNode* build(vector<int>& preorder, vector<int>& inorder, int pl, int pr, int il, int ir) {
        if (pl > pr) return nullptr;
        auto root = new TreeNode(preorder[pl]);
        int mid = pos[root->val], llen = mid - il, rlen = ir - mid;
        root->left = build(preorder, inorder, pl + 1, pl + llen, il, mid - 1);
        root->right = build(preorder, inorder, pl + llen + 1, pr, mid + 1, ir);
        return root;
    }
};

106. 从中序与后序遍历序列构造二叉树

根据一棵树的中序遍历与后序遍历构造二叉树。

注意:
你可以假设树中没有重复的元素。

例如，给出

1
2
中序遍历 inorder = [9,3,15,20,7]
后序遍历 postorder = [9,15,7,20,3]

返回如下的二叉树：

1
2
3
4
/ \
  9  20
    /  \
   15   7

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    unordered_map<int, int> pos;
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        for (int i = 0; i < inorder.size(); ++i) pos[inorder[i]] = i;
        return build(inorder, postorder, 0, inorder.size() - 1, 0, postorder.size() - 1);
    }

    TreeNode* build(vector<int> &inorder, vector<int> &postorder, int il, int ir, int pl, int pr) {
        if (il > ir) return nullptr;
        auto root = new TreeNode(postorder[pr]);
        auto mid = pos[root->val], llen = mid - il, rlen = ir - mid;
        root->left = build(inorder, postorder, il, mid - 1, pl, pl + llen - 1);
        root->right = build(inorder, postorder, mid + 1, ir, pr - rlen, pr - 1);
        return root;
    }
};

108. 将有序数组转换为平衡二叉搜索树

给你一个整数数组 nums ，其中元素已经按 升序 排列，请你将其转换为一棵 高度平衡 二叉搜索树。

高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。

示例 1：

1
2
3
输入：nums = [-10,-3,0,5,9]
输出：[0,-3,9,-10,null,5]
解释：[0,-10,5,null,-3,null,9] 也将被视为正确答案：

示例 2：

1
2
3
输入：nums = [1,3]
输出：[3,1]
解释：[1,3] 和 [3,1] 都是高度平衡二叉搜索树。

提示：

  • 1 <= nums.length <= 104
  • -104 <= nums[i] <= 104
  • nums 按 严格递增 顺序排列

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    TreeNode* sortedArrayToBST(vector<int>& nums) {
        return build(nums, 0, nums.size() - 1);
    }

    TreeNode* build(vector<int> &nums, int l, int r) {
        if (l > r) return nullptr;
        int mid = l + r >> 1;
        auto root = new TreeNode(nums[mid]);
        root->left = build(nums, l, mid - 1);
        root->right = build(nums, mid + 1, r);
        return root;
    }
};

109. 有序链表转换平衡二叉搜索树

给定一个单链表，其中的元素按升序排序，将其转换为高度平衡的二叉搜索树。

本题中，一个高度平衡二叉树是指一个二叉树_每个节点_ 的左右两个子树的高度差的绝对值不超过 1。

示例:

1
2
3
4
5
6
7
8
给定的有序链表： [-10, -3, 0, 5, 9],

一个可能的答案是：[0, -3, 9, -10, null, 5], 它可以表示下面这个高度平衡二叉搜索树：

     / \
   -3   9
   /   /
 -10  5

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    TreeNode* sortedListToBST(ListNode* head) {
        if (!head) return nullptr;

        int n = 0;
        for (auto p = head; p; p = p->next) ++n;

        if (n == 1) return new TreeNode(head->val);

        int mid = n / 2;
        auto cur = head;
        for (int i = 0; i < mid - 1; ++i) cur = cur->next; // 前面一个
        auto now = cur->next;
        cur->next = nullptr;

        auto root = new TreeNode(now->val);
        root->left = sortedListToBST(head);
        root->right = sortedListToBST(now->next);
        return root;
    }
};

95. 不同的二叉搜索树 II

难度中等 1099

给你一个整数 n ，请你生成并返回所有由 n 个节点组成且节点值从 1 到 n 互不相同的不同 二叉搜索树 。可以按 任意顺序 返回答案。

示例 1：

1
2
输入：n = 3
输出：[[1,null,2,null,3],[1,null,3,2],[2,1,3],[3,1,null,null,2],[3,2,null,1]]

示例 2：

1
2
输入：n = 1
输出：[[1]]

提示：

  • 1 <= n <= 8

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    vector<TreeNode*> generateTrees(int n) {
        return dfs(1, n);
    }

    vector<TreeNode*> dfs(int l, int r) {
        if (l > r) return {nullptr};
        vector<TreeNode*> ans;

        for (int i = l; i <= r; ++i) { //枚举根节点位置
            auto left = dfs(l, i - 1), right = dfs(i + 1, r);
            for (auto l : left) {
                for (auto r : right) {
                    auto root = new TreeNode(i); //生成根节点
                    root->left = l, root->right = r;
                    ans.push_back(root);
                }
            }
        }   

        return ans;
    }
};