参考《算法竞赛进阶指南》 、AcWing题库
前缀和与差分
前缀和
对于一个给定的数列 A A A S S S
S [ i ] = ∑ j = 1 i A [ j ] S[i]=\sum_{j=1}^{i} A[j]
S [ i ] = j = 1 ∑ i A [ j ]
一个部分和, 即数列 A A A
sum ( l , r ) = ∑ i = 1 r A [ i ] = S [ r ] − S [ l − 1 ] \operatorname{sum}(l, r)=\sum_{i=1}^{r} A[i]=S[r]-S[l-1]
sum ( l , r ) = i = 1 ∑ r A [ i ] = S [ r ] − S [ l − 1 ]
在二维数组 (矩阵) 中, 可类似地求出二维前缀和, 进一步计算出二维部分和。
地图上有 N N N X i , Y i X_{i}, Y_{i} X i , Y i W i W_i W i
注意 :不同目标可能在同一位置。
现在有一种新型的激光炸弹,可以摧毁一个包含 R × R R \times R R × R
激光炸弹的投放是通过卫星定位的,但其有一个缺点,就是其爆炸范围,即那个正方形的边必须和 x , y x,y x , y
求一颗炸弹最多能炸掉地图上总价值为多少的目标。
输入格式
第一行输入正整数 N N N R R R
接下来 N N N X i , Y i , W i X_{i}, Y_{i}, W_{i} X i , Y i , W i x x x y y y
输出格式
输出一个正整数,代表一颗炸弹最多能炸掉地图上目标的总价值数目。
数据范围
0 ≤ R ≤ 1 0 9 0 \le R \le 10^9 0 ≤ R ≤ 1 0 9 0 < N ≤ 10000 0 < N \le 10000 0 < N ≤ 10000 0 ≤ X i , Y i ≤ 5000 0 \le X_{i}, Y_{i} \le 5000 0 ≤ X i , Y i ≤ 5000 0 ≤ W i ≤ 1000 0 \le W_i \le 1000 0 ≤ W i ≤ 1000
输入样例:
输出样例:
算法分析
因为 X i , Y i X_{i}, Y_{i} X i , Y i 0 ∼ 5000 0 \sim 5000 0 ∼ 5000 A A A A [ i , j ] A[i, j] A [ i , j ] ( i , j ) (i, j) ( i , j ) A [ X i , Y i ] + = W i A\left[X_{i}, Y_{i}\right]+=W_{i} A [ X i , Y i ] + = W i A A A S S S
S [ i , j ] = ∑ x = 1 i ∑ y = 1 j A [ x , y ] S[i, j]=\sum_{x=1}^{i} \sum_{y=1}^{j} A[x, y]
S [ i , j ] = x = 1 ∑ i y = 1 ∑ j A [ x , y ]
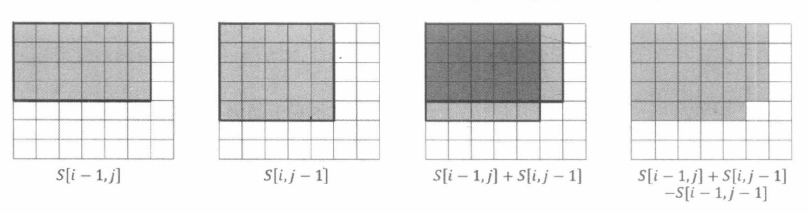
如下图所示, 我们再观察 S [ i , j ] , S [ i − 1 , j ] , S [ i , j − 1 ] , S [ i − 1 , j − 1 ] S[i, j], S[i-1, j], S[i, j-1], S[i-1, j-1] S [ i , j ] , S [ i − 1 , j ] , S [ i , j − 1 ] , S [ i − 1 , j − 1 ]
容易得到如下的递推式:
S [ i , j ] = S [ i − 1 , j ] + S [ i , j − 1 ] − S [ i − 1 , j − 1 ] + A [ i , j ] S[i, j]=S[i-1, j]+S[i, j-1]-S[i-1, j-1]+A[i, j]
S [ i , j ] = S [ i − 1 , j ] + S [ i , j − 1 ] − S [ i − 1 , j − 1 ] + A [ i , j ]
同理, 对于任意一个边长为 R R R
∑ x = i − R + 1 i ∑ y = j − R + 1 j A [ x , y ] = S [ i , j ] − S [ i − R , j ] − S [ i , j − R ] + S [ i − R , j − R ] \sum_{x=i-R+1}^{i} \sum_{y=j-R+1}^{j} A[x, y]=S[i, j]-S[i-R, j]-S[i, j-R]+S[i-R, j-R]
x = i − R + 1 ∑ i y = j − R + 1 ∑ j A [ x , y ] = S [ i , j ] − S [ i − R , j ] − S [ i , j − R ] + S [ i − R , j − R ]
因此, 我们只需要 O ( N 2 ) O\left(N^{2}\right) O ( N 2 ) S S S O ( N 2 ) O\left(N^{2}\right) O ( N 2 ) R R R ( i , j ) (i, j) ( i , j ) O ( 1 ) O(1) O ( 1 )
值得一提的是, 上面我们把 ( X i , Y i ) \left(X_{i}, Y_{i}\right) ( X i , Y i ) ( X i , Y i ) \left(X_{i}, Y_{i}\right) ( X i , Y i ) ( X i , Y i ) \left(X_{i}, Y_{i}\right) ( X i , Y i ) ( X i − 0.5 , Y i − 0.5 ) \left(X_{i}-0.5, Y_{i}-0.5\right) ( X i − 0.5 , Y i − 0.5 ) ( X i + 0.5 , Y i + 0.5 ) \left(X_{i}+0.5, Y_{i}+0.5\right) ( X i + 0.5 , Y i + 0.5 ) □ . 5 \square .5 □ .5 A A A S S S
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 #include <cstdio> #include <cstring> #include <iostream> #include <algorithm> using namespace std;const int N = 5006 ;int n, r, s[N][N];int main () memset (s, 0 , sizeof cin >> n >> r; while (n--) { int x, y, z; scanf ("%d %d %d" , &x, &y, &z); s[x][y] += z; } for (int i = 0 ; i <= 5000 ; i++) for (int j = 0 ; j <= 5000 ; j++) if (!i && !j) continue ; else if (!i) s[i][j] += s[i][j-1 ]; else if (!j) s[i][j] += s[i-1 ][j]; else s[i][j] += s[i-1 ][j] + s[i][j-1 ] - s[i-1 ][j-1 ]; int ans = 0 ; if (r<5001 ){ for (int i = r - 1 ; i <= 5000 ; i++) for (int j = r - 1 ; j <= 5000 ; j++) if (i == r - 1 && j == r - 1 ) ans = max (ans, s[i][j]); else if (i == r - 1 ) ans = max (ans, s[i][j] - s[i][j-r]); else if (j == r - 1 ) ans = max (ans, s[i][j] - s[i-r][j]); else ans = max (ans, s[i][j] - s[i-r][j] - s[i][j-r] + s[i-r][j-r]); } else { ans=s[5000 ][5000 ]; } cout << ans << endl; return 0 ; }
Solution
差分
对于一个给定的数列 A A A B B B
B [ 1 ] = A [ 1 ] , B [ i ] = A [ i ] − A [ i − 1 ] ( 2 ≤ i ≤ n ) B[1]=A[1], \quad B[i]=A[i]-A[i-1](2 \leq i \leq n)
B [ 1 ] = A [ 1 ] , B [ i ] = A [ i ] − A [ i − 1 ] ( 2 ≤ i ≤ n )
容易发现, “前缀和”与 “差分” 是一对互逆运算, 差分序列 B B B A A A S S S A A A
把序列 A A A [ l , r ] [l, r] [ l , r ] d d d A l , A l + 1 , ⋯ , A r A_{l}, A_{l+1}, \cdots, A_{r} A l , A l + 1 , ⋯ , A r d d d B B B B l B_{l} B l d , B r + 1 d, B_{r+1} d , B r + 1 d d d
在 数的直径与最近公共祖先 中, 我们还会继续探讨差分技巧在树上的应用。
给定一个长度为 n n n a 1 , a 2 , … , a n {a_1,a_2,…,a_n} a 1 , a 2 , … , a n [ l , r ] [l,r] [ l , r ]
求至少需要多少次操作才能使数列中的所有数都一样,并求出在保证最少次数的前提下,最终得到的数列可能有多少种。
输入格式
第一行输入正整数 n n n
接下来 n n n i + 1 i+1 i + 1 a i a_i a i
输出格式
第一行输出最少操作次数。
第二行输出最终能得到多少种结果。
数据范围
0 < n ≤ 1 0 5 0 < n \le 10^5 0 < n ≤ 1 0 5 0 ≤ a i < 2147483648 0 \le a_i <2147483648 0 ≤ a i < 2147483648
输入样例:
输出样例:
算法分析
求出 a a a b b b b 1 = a 1 , b i = a i − a i − 1 ( 2 ≤ i ≤ n ) b_{1}=a_{1}, b_{i}=a_{i}-a_{i-1}(2 \leq i \leq n) b 1 = a 1 , b i = a i − a i − 1 ( 2 ≤ i ≤ n ) b n + 1 = 0 b_{n+1}=0 b n + 1 = 0 a a a b 1 , b 2 , ⋯ , b n + 1 b_{1}, b_{2}, \cdots, b_{n+1} b 1 , b 2 , ⋯ , b n + 1 b 2 , b 3 , ⋯ , b n b_{2}, b_{3}, \cdots, b_{n} b 2 , b 3 , ⋯ , b n a a a n n n b 1 b_{1} b 1
从 b 1 , b 2 , ⋯ , b n + 1 b_{1}, b_{2}, \cdots, b_{n+1} b 1 , b 2 , ⋯ , b n + 1
选 b i b_{i} b i b j b_{j} b j 2 ≤ i , j ≤ n 2 \leq i, j \leq n 2 ≤ i , j ≤ n b 2 , b 3 , ⋯ , b n b_{2}, b_{3}, \cdots, b_{n} b 2 , b 3 , ⋯ , b n b i b_{i} b i b j b_{j} b j
选 b 1 b_{1} b 1 b j b_{j} b j 2 ≤ j ≤ n 2 \leq j \leq n 2 ≤ j ≤ n
选 b i b_{i} b i b n + 1 b_{n+1} b n + 1 2 ≤ i ≤ n 2 \leq i \leq n 2 ≤ i ≤ n
选 b 1 b_{1} b 1 b n + 1 b_{n+1} b n + 1 b 2 , b 3 , ⋯ , b n b_{2}, b_{3}, \cdots, b_{n} b 2 , b 3 , ⋯ , b n
设 b 2 , b 3 , ⋯ , b n b_{2}, b_{3}, \cdots, b_{n} b 2 , b 3 , ⋯ , b n p p p q q q min ( p , q ) \min (p, q) min ( p , q ) ∣ p − q ∣ |p-q| ∣ p − q ∣ b 1 b_{1} b 1 b n + 1 b_{n+1} b n + 1 ∣ p − q ∣ |p-q| ∣ p − q ∣
综上所述, 最少操作次数为 min ( p , q ) + ∣ p − q ∣ = max ( p , q ) \min (p, q)+|p-q|=\max (p, q) min ( p , q ) + ∣ p − q ∣ = max ( p , q ) ∣ p − q ∣ |p-q| ∣ p − q ∣ ∣ p − q ∣ + 1 |p-q|+1 ∣ p − q ∣ + 1 b 1 b_{1} b 1 a a a ∣ p − q ∣ + 1 |p-q|+1 ∣ p − q ∣ + 1
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 #include <cmath> #include <cstdio> #include <iostream> #define ll long long using namespace std;const int N = 100006 ;ll a[N], b[N]; int main () int n; cin >> n; for (int i = 1 ; i <= n; i++) scanf ("%lld" , &a[i]); b[1 ] = a[1 ]; for (int i = 2 ; i <= n; i++) b[i] = a[i] - a[i-1 ]; ll p = 0 , q = 0 ; for (int i = 2 ; i <= n; i++) if (b[i] > 0 ) p += b[i]; else if (b[i] < 0 ) q -= b[i]; cout << max (p, q) << endl << abs (p - q) + 1 << endl; return 0 ; }
Solution
有 N N N 1 、 2 、 3 … N 1、2、3…N 1 、 2 、 3 … N
当且仅当两头牛中间的牛身高都比它们矮时,两头牛方可看到对方。
现在,我们只知道其中最高的牛是第 P P P H H H
但是,我们还知道这群牛之中存在着 M M M A A A B B B
求每头牛的身高的最大可能值是多少。
输入格式
第一行输入整数 N , P , H , M N, P, H, M N , P , H , M
接下来 M M M A A A B B B A A A B B B
输出格式
一共输出 N N N
第 i i i i i i
数据范围
1 ≤ N ≤ 10000 1 \le N \le 10000 1 ≤ N ≤ 10000 1 ≤ H ≤ 1000000 1 \le H \le 1000000 1 ≤ H ≤ 1000000 1 ≤ A , B ≤ 10000 1 \le A,B \le 10000 1 ≤ A , B ≤ 10000 0 ≤ M ≤ 10000 0 \le M \le 10000 0 ≤ M ≤ 10000
输入样例:
1 2 3 4 5 6 9 3 5 5 1 3 5 3 4 3 3 7 9 8
输出样例:
注意:
算法分析
题目中的 M M M C C C A i A_{i} A i B i B_{i} B i A i < B i A_{i}<B_{i} A i < B i C C C A i + 1 A_{i}+1 A i + 1 B i − 1 B_{i}-1 B i − 1 A i A_{i} A i B i B_{i} B i P P P C [ P ] C[P] C [ P ] P P P C C C i i i H + C [ i ] H+C[i] H + C [ i ]
如果我们朴素执行把数组 C C C A i + 1 A_{i}+1 A i + 1 B i − 1 B_{i}-1 B i − 1 O ( N M ) O(N M) O ( NM ) D D D A i A_{i} A i B i B_{i} B i D [ A i + 1 ] D\left[A_{i}+1\right] D [ A i + 1 ] 1 , D [ B i ] 1, D\left[B_{i}\right] 1 , D [ B i ] A i + 1 A_{i}+1 A i + 1 B i − 1 B_{i}-1 B i − 1 B i B_{i} B i C C C D D D C [ i ] = ∑ j = 1 i D [ j ] C[i]=\sum_{j=1}^{i} D[j] C [ i ] = ∑ j = 1 i D [ j ]
上述优化后的算法把对一个区间的操作转化为左、右两个端点上的操作 , 再通过前缀和得到原问题的解。这种思想很常用, 我们在后面还会多次遇到。该算法的时间复杂度为 O ( N + M ) \mathrm{O}(N+M) O ( N + M )
值得提醒的是, 在本题的数据中, 一条关系 ( A i , B i ) \left(A_{i}, B_{i}\right) ( A i , B i )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 #include <map> #include <cstdio> #include <cstring> #include <iostream> #include <algorithm> using namespace std;map<pair<int , int >, bool > v; const int N = 10006 ;int s[N];int main () int n, p, h, t; cin >> n >> p >> h >> t; memset (s, 0 , sizeof while (t--) { int a, b; scanf ("%d %d" , &a, &b); if (a > b) swap (a, b); if (v[make_pair (a, b)]) continue ; s[a+1 ]--; s[b]++; v[make_pair (a, b)] = 1 ; } int ans = 0 ; for (int i = 1 ; i <= n; i++) { ans += s[i]; printf ("%d\n" , h + ans); } return 0 ; }
Solution