参考《算法竞赛进阶指南》、AcWing题库

递推与递归

一个实际问题的各种可能情况构成的集合通常称为 “状态空间”, 而程序的运行则是对于状态空间的遍历, 算法和数据结构则通过划分、归纳、提取、抽象来帮助提高程序遍历状态空间的效率。递推和递归就是程序遍历状态空间的两种基本方式。

递推与递归的宏观描述

对于一个待求解的问题, 当它局限在某处边界、某个小范围或者某种特殊情形下时, 其答案往往是已知的。如果能够将该解答的应用场景扩大到原问题的状态空间, 并且扩展过程的每个步骤具有相似性, 就可以考虑使用递推或者递归求解。

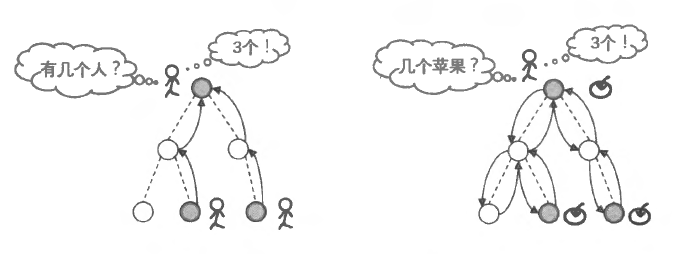
以已知的 “问题边界” 为起点向 “原问题” 正向推导的扩展方式就是递推。然而在很多时候, 推导的路线难以确定, 这时以 “原问题” 为起点尝试寻找把状态空问缩小到已知的 “问题边界” 的路线, 再通过该路线反向回溯的遍历方式就是递归。我们通过两幅图来表示递推与递归的差别。

我们刚才也提到, 使用递推或递归要求 “原问题” 与 “问题边界” 之间的每个变换步骤具有相似性, 这样我们才能够设计一段程序实现这个步骤, 将其重复作用于问题之中。换句话说, 程序在每个步骤上应该面对相同种类的问题, 这些问题都是原问题的一个子问题, 可能仅在规模或者某些限制条件上有所区别, 并且能够使用 “求解原问题的程序” 进行求解。

对于递归算法，有 了上面这个前提，我们就可以让程序在每个变换步骤中执行三个操作:

  1. 缩小问题状态空间的规模。这意味着程序尝试寻找在 “原问题” 与 “问题边界” 之间的变换路线, 并向正在探索的路线上迈出一步。
  2. 尝试求解规模缩小以后的问题, 结果可能是成功, 也可能是失败。
  3. 如果成功, 即找到了规模缩小后的问题的答案, 那么将答案扩展到当前问题。如果失败, 那么重新回到当前问题, 程序可能会继续寻找当前问题的其他变换路线, 直至最终确定当前问题无法求解。

在以上三个操作中有两点颇为关键。

一是 “如何尝试求解规模缩小以后的问题”。因为规模缩小以后的问题是原问题的一个子问题, 所以我们可以把它视为一个新的 “原问题” 由相同的程序 (上述三个操作）进行求解, 这就是所谓的 “自身调用自身”。

二是如果求解子问题失败, 程序需要重新回到当前问题去寻找其他的变换路线, 因此把当前问题缩小为子问题时所做的对当前问题状态产生影响的事情应该全部失效, 这就是所谓的 “回溯时还原现场”。

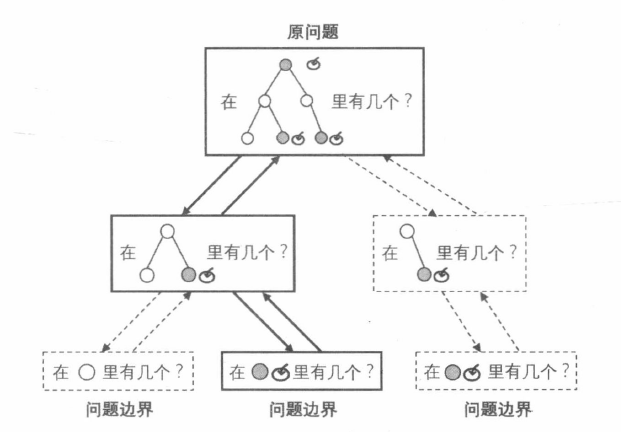
上面这类程序就是 “递归” 的遍历方式, 其整体流程如下图所示。

可以看到, 递归程序的基本单元是由 “缩小” “求解” “扩展” 组成的一种变换步骤, 只是在 “求解” 时因为问题的相似性, 不断重复使用了这样一种变换步骤, 直至在已知的问题边界上直接确定答案。对于其中任意一条从 “原问题” 到 “问题边界” 的变换路线 (图中实线圈出的路径), 横向来看, 它的每一层是一次递归程序体的执行; 纵向来看, 它的左右两边分别是寻找路线和沿其推导的流程。为了保证每层的 “缩小” 与 “扩展” 能够衔接在同一形式的问题上, “求解” 操作自然要保证在执行前后程序面对问题的状态是相同的, 这也就是 “还原现场” 的必要性所在。

递推与递归的简单应用

在使用枚举算法蛮力探索问题的整个 “状态空间” 时, 经常需要递归。按照规模大小, 有如下几种常见的枚举形式和遍历方式:

枚举形式 状态空间规模 一般遍历方式
多项式 nk,  kn^k,\;k 为常数 循环(for)、递推
指 数 kn,  kk^{n},\;k 为常数 递归、位运算
排 列 n!n! 递归、C++ next_permutation
组 合 CnmC_n^{m} 递归+剪枝

“多项式” 型的枚举在程序设计中随处可见。
位运算中的最短 Hamilton 路径问题的朴素做法, 是一种 “排列” 型的枚举。
例题 “费解的开关” 中的枚举则是一 种 “指数” 型的枚举。

92. 递归实现指数型枚举

从 1∼n1 \sim n 这 nn 个整数中随机选取任意多个，输出所有可能的选择方案。

输入格式

输入一个整数 nn。

输出格式

每行输出一种方案。

同一行内的数必须升序排列，相邻两个数用恰好 11 个空格隔开。

对于没有选任何数的方案，输出空行。

本题有自定义校验器（SPJ），各行（不同方案）之间的顺序任意。

数据范围

1≤n≤151 \le n \le 15

输入样例：

1
3

输出样例：

1
2
3
4
5
6
7
3
2
2 3
1
1 3
1 2
1 2 3

算法分析

这等价于每个整数可以选可以不选, 所有可能的方案总数共有 2n2^{n} 种。我们已经知道可以进行一次循环, 利用位运算来列举所有的选择方案。这一次我们使用递归来求解, 在每次递归中分别尝试某个数 “选” 或 “不选” 两条分支, 将尚未确定的整数数量减少 1 , 从而转化为一个规模更小的同类问题。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
// 递归实现指数型枚举
vector<int> chosen; // 被选择的数
void calc(int x) {
	if (x == n + 1) { // 问题边界
		for (int i = 0; i < chosen.size(); i++)
			printf("%d ", chosen[i]);
		puts("");
		return;
	}
	// “不选 x ” 分支
	calc(x + 1); // 求解子问题
	
	// “选 x ” 分支
	chosen.push_back(x); // 记录 x 已被选择
	calc(x + 1); // 求解子问题
	chosen.pop_back(); // 准备回溯到上一问题之前，还原现场
}
int main() {
	calc(1); // 主函数的调用入口
}

Solution

93. 递归实现组合型枚举

从 1∼n1 \sim n 这 nn 个整数中随机选出 mm 个，输出所有可能的选择方案。

输入格式

两个整数 n,mn, m ,在同一行用空格隔开。

输出格式

按照从小到大的顺序输出所有方案，每行 11 个。

首先，同一行内的数升序排列，相邻两个数用一个空格隔开。

其次，对于两个不同的行，对应下标的数一一比较，字典序较小的排在前面（例如 1 3 5 7 排在 1 3 6 8 前面）。

数据范围

n>0n>0 ,
0≤m≤n0 \le m \le n ,
n+(n−m)≤25n+(n-m) \le 25

输入样例：

1
5 3

输出样例：

1
2
3
4
5
6
7
8
9
10
1 2 3 
1 2 4 
1 2 5 
1 3 4 
1 3 5 
1 4 5 
2 3 4 
2 3 5 
2 4 5 
3 4 5

思考题：如果要求使用非递归方法，该怎么做呢？

算法分析

我们只需要在上面指数型枚举的程序的 calc 函数开头添加以下这条语句即可：

1
if (chosen.size() > m || chosen.size() + (n - x + 1) < m) return;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
// 递归实现组合型枚举
vector<int> chosen; 
void calc(int x) {
	if (chosen.size() > m || chosen.size() + (n - x + 1) < m) return;
	if (x == n + 1) {
		for (int i = 0; i < chosen.size(); i++)
			printf("%d ", chosen[i]);
		puts("");
		return;
	}
	calc(x + 1);
	chosen.push_back(x);
	calc(x + 1);
	chosen.pop_back();
}

这就是所谓的 “剪枝” 。寻找变换路线其实就是 “搜索” 的过程, 如果能够及时确定当前问题一定是无解的, 就不需要到达问题边界才返回结果。在本题中, 如果已经选择了超过 mm 个数, 或者即使再选上剩余所有的数也不够 mm 个, 就可以提前得知当前问题无解了。这条剪枝保证我们一旦进入无解的分支就会立刻返回, 所以时间复杂度就 从 2n2^{n} 降低为 CnmC_{n}^{m} 。

Solution

94. 递归实现排列型枚举

算法分析

该问题也被称为全排列问题, 所有可能的方案总数有 n!n ! 种。在这里, 递归需要求解的问题是 “把指定的 nn 个整数按照任意次序排列”, 在每次递归中, 我们尝试把每个可用的数作为数列中的下一个数, 求解 “把剩余的 n−1n-1 个整数按照任意次序排列” 这个规模更小的子问题。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>
using namespace std;
int n;
int order[20]; // 按顺序依次记录被选择的整数
bool chosen[20]; // 标记被选择的整数
void calc(int k) {
	if (k == n + 1) { // 问题边界
		for (int i = 1; i <= n; i++)
			printf("%d ", order[i]);
		puts("");
		return;
	}
	for (int i = 1; i <= n; i++) { 
		if (chosen[i]) continue;
		order[k] = i;
		chosen[i] = 1;
		calc(k + 1); 
		chosen[i] = 0;
		order[k] = 0; // 这一行可以省略
	}
}
int main() { 
	cin >> n;
	calc(1);  // 主函数中的调用入口
}

Solution

95. 费解的开关

你玩过“拉灯”游戏吗？

2525 盏灯排成一个 5×55 \times 5 的方形。

每一个灯都有一个开关，游戏者可以改变它的状态。

每一步，游戏者可以改变某一个灯的状态。

游戏者改变一个灯的状态会产生连锁反应：和这个灯上下左右相邻的灯也要相应地改变其状态。

我们用数字 11 表示一盏开着的灯，用数字 00 表示关着的灯。

下面这种状态

1
2
3
4
5
10111
01101
10111
10000
11011

在改变了最左上角的灯的状态后将变成：

1
2
3
4
5
01111
11101
10111
10000
11011

再改变它正中间的灯后状态将变成：

1
2
3
4
5
01111
11001
11001
10100
11011

给定一些游戏的初始状态，编写程序判断游戏者是否可能在 66 步以内使所有的灯都变亮。

输入格式

第一行输入正整数 nn，代表数据中共有 nn 个待解决的游戏初始状态。

以下若干行数据分为 nn 组，每组数据有 55 行，每行 55 个字符。

每组数据描述了一个游戏的初始状态。

各组数据间用一个空行分隔。

输出格式

一共输出 nn 行数据，每行有一个小于等于 66 的整数，它表示对于输入数据中对应的游戏状态最少需要几步才能使所有灯变亮。

对于某一个游戏初始状态，若 66 步以内无法使所有灯变亮，则输出 −1-1。

数据范围

0<n≤5000 < n \le 500

输入样例：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
3
00111
01011
10001
11010
11100

11101
11101
11110
11111
11111

01111
11111
11111
11111
11111

输出样例：

1
2
3
3
2
-1

算法分析

在上述规则的 01 矩阵的点击游戏中, 很容易发现三个性质:

  1. 每个位置至多只会被点击一次。
  2. 若固定了第一行 (不能再改变第一行), 则满足题意的点击方案至多只有 1 种。 其原因是：当第 ii 行某一位为 1 时, 若前 ii 行已被固定, 只能点击第 i+1i+1 行该位置上的数字才能使第 ii 行的这一位变成 0 。从上到下按行使用归纳法可得上述结论。
  3. 点击的先后顺序不影响最终结果。

于是, 我们不妨先考虑第一行如何点击。在枚举第一行的点击方法 ( 25=322^{5}=32 种 ) 后, 就可以认为第一行 “固定不动”, 再考虑第 2∼52 \sim 5 行如何点击。而按照上述性质 2 , 此时第 2∼52 \sim 5 行的点击方案是确定的一一从第一行开始递推, 当第 ii 行某一位为 1 时, 点击第 i+1i+1 行该位置上的数字。若到达第 nn 行时不全为 0 , 说明这种点击方式不合法。在所有合法的点击方式中取点击次数最少的就是答案。对第一行的 32 次枚举涵盖了该问题的整个状态空间, 因此该做法是正确的。

对于第一行点击方法的枚举, 可以采用位运算的方式, 枚举 0∼310 \sim 31 这 32 个 5 位二进制数, 若二进制数的第 k(0≤k<5)k(0 \leq k<5) 位为 1 , 就点击 01 矩阵第 1 行第 k+1k+1 列的 数字。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
#include <cstring>
#include <iostream>
using namespace std;
const int N = 6;
int a[N], ans, aa[N];
char s[N];

void dj(int x, int y) {
	aa[x] ^= (1 << y);
	if (x != 1) aa[x-1] ^= (1 << y);
	if (x != 5) aa[x+1] ^= (1 << y);
	if (y != 0) aa[x] ^= (1 << (y - 1));
	if (y != 4) aa[x] ^= (1 << (y + 1));
}

void pd(int p) {
	int k = 0;
	memcpy(aa, a, sizeof(a));
	for (int i = 0; i < 5; i++)
		if (!((p >> i) & 1)) {
			dj(1, i);
			if (++k >= ans) return;
		}
	for (int x = 1; x < 5; x++)
		for (int y = 0; y < 5; y++)
			if (!((aa[x] >> y) & 1)) {
				dj(x + 1, y);
				if (++k >= ans) return;
			}
	if (aa[5] == 31) ans = k;
}

void abc() {
	memset(a, 0, sizeof(a));
	for (int i = 1; i <= 5; i++) {
		cin >> (s + 1);
		for (int j = 1; j <= 5; j++) a[i] = a[i] * 2 + (s[j] - '0');
	}
	ans = 7;
	for (int p = 0; p < (1 << 5); p++) pd(p);
	if (ans == 7) cout << "-1" << endl;
	else cout << ans << endl;
}

int main() {
	int n;
	cin >> n;
	while (n--) abc();
	return 0;
}

Solution

96. 奇怪的汉诺塔

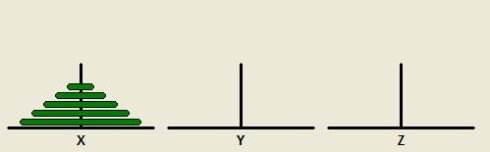
汉诺塔问题，条件如下：

1、这里有 A、B、CA、B、C 和 DD 四座塔。

2、这里有 nn 个圆盘，nn 的数量是恒定的。

3、每个圆盘的尺寸都不相同。

4、所有的圆盘在开始时都堆叠在塔 AA 上，且圆盘尺寸从塔顶到塔底逐渐增大。

5、我们需要将所有的圆盘都从塔 AA 转移到塔 DD 上。

6、每次可以移动一个圆盘，当塔为空塔或者塔顶圆盘尺寸大于被移动圆盘时，可将圆盘移至这座塔上。

请你求出将所有圆盘从塔 AA 移动到塔 DD，所需的最小移动次数是多少。

输入格式

没有输入

输出格式

对于每一个整数 nn，输出一个满足条件的最小移动次数，每个结果占一行。

数据范围

1≤n≤121 \le n \le 12

输入样例：

1
没有输入

输出样例：

1
参考输出格式

算法分析

首先考虑 nn 个盘子 3 座塔的经典 Hanoi 问题, 设 d[n]d[n] 表示求解该 nn 盘 3 塔问题的最少步数, 显然有 d[n]=2∗d[n−1]+1d[n]=2 * d[n-1]+1, 即把前 n−1n-1 个盘子从 A 柱移动到 B\mathrm{B} 柱, 然后把第 nn 个盘子从 A\mathrm{A} 柱移动到 C\mathrm{C} 柱, 最后把前 n−1n-1 个盘子从 B\mathrm{B} 柱移动到 C 柱。

回到本题, 设 f[n]f[n] 表示求解 nn 盘 4 塔问题的最少步数, 则:

f[n]=min⁡1≤i<n{2∗f[i]+d[n−i]}f[n]=\min _{1 \leq i<n}\{2 * f[i]+d[n-i]\}

其中 f[1]=1f[1]=1 。上式的含义是, 先把 ii 个盘子在 4 塔模式下移动到 B\mathrm{B} 柱, 然后把 n−in-i 个盘子在 3 塔模式下移动到 D 柱, 最后把 ii 个盘子在 4 塔模式下移动到 D 柱。考虑所有可能的 ii 取最小值, 就得到了上述递推公式。

在时间复杂度可以接受的前提下, 上述做法可以推广到 nn 盘 mm 塔的计算。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
//Author:XuHt
#include <cstring>
#include <iostream>
#include <algorithm>
#define ll long long
using namespace std;
const int N = 15;
ll d[N], f[N];

int main() {
	int n = 12;
	memset(f, 0x3f, sizeof(f));
	d[1] = f[1] = 1;
	for (int i = 2; i <= n; i++) d[i] = 2 * d[i-1] + 1;
	for (int i = 2; i <= n; i++)
		for (int j = 1; j < i; j++)
			f[i] = min(f[i], 2 * f[j] + d[i-j]);
	for (int i = 1; i <= n; i++) cout << f[i] << endl;
	return 0;
}

Solution

分治

分治法把一个问题划分为若干个规模更小的同类子问题, 对这些子问题递归求解, 然后在回溯时通过它们推导出原问题的解。

97. 约数之和

假设现在有两个自然数 AA 和 BB，SS 是 ABA^B 的所有约数之和。

请你求出 S mod 9901S \bmod 9901 的值是多少。

输入格式

在一行中输入用空格隔开的两个整数 AA 和 BB。

输出格式

输出一个整数，代表 S mod 9901S \bmod 9901 的值。

数据范围

0≤A,B≤5×1070 \le A,B \le 5 \times 10^7

输入样例：

1
2 3

输出样例：

1
15

注意: AA 和 BB 不会同时为 00。

算法分析

把 AA 分解质因数, 表示为 p1c1∗p2c2∗⋯∗pncnp_{1}^{c_{1}} * p_{2}^{c_{2}} * \cdots * p_{n}^{c_{n}} 。那么 ABA^{B} 表示为 p1B∗c1∗p2B∗c2∗⋯∗pnB∗cnp_{1}^{B * c_{1}} * p_{2}^{B * c_{2}} * \cdots * p_{n}^{B * c_{n}} 。ABA^{B} 的所有约数表示为集合 {p1k1∗p2k2∗⋯∗pnkn}\left\{p_{1}^{k_{1}} * p_{2}^{k_{2}} * \cdots * p_{n}^{k_{n}}\right\}, 其中 0≤ki≤B∗ci(1≤i≤n)0 \leq k_{i} \leq B * c_{i}(1 \leq i \leq n) 。

根据乘法分配律, ABA^{B} 的所有约数之和就是:

(1+p1+p12+⋯+p1B∗c1)∗(1+p2+p22+⋯+p2B∗c2)∗⋯∗(1+pn+pn2+⋯+pnB∗cn)\begin{gathered} \left(1+p_{1}+p_{1}^{2}+\cdots+p_{1}^{B * c_{1}}\right) *\left(1+p_{2}+p_{2}^{2}+\cdots+p_{2}^{B * c_{2}}\right) * \cdots \\ *\left(1+p_{n}+p_{n}^{2}+\cdots+p_{n}^{B * c_{n}}\right) \end{gathered}

我们可以把该式展开, 与约数集合比较。

上式中的每个括号内都是等比数列, 如果使用等比数列求和公式, 需要做除法。而答案还需要对 9901 取模, mod 运算只对加、减、乘有分配率, 不能直接对分子、分母分别取模后再做除法。我们可以换一种思路, 使用分治法进行等比数列求和。

问题: 使用分治法求 sum⁡(p,c)=1+p+p2+⋯+pc=?\operatorname{sum}(p, c)=1+p+p^{2}+\cdots+p^{c}=?

若 cc 为奇数:

sum⁡(p,c)=(1+p+⋯+pc−12)+(pc+12+⋯+pc)=(1+p+⋯+pc−12)+pc+12∗(1+p+⋯+pc−12)=(1+pc+12)∗sum⁡(p,c−12)\begin{aligned} \operatorname{sum}(p, c)=(1&\left.+p+\cdots+p^{\frac{c-1}{2}}\right)+\left(p^{\frac{c+1}{2}}+\cdots+p^{c}\right) \\ &=\left(1+p+\cdots+p^{\frac{c-1}{2}}\right)+p^{\frac{c+1}{2}} *\left(1+p+\cdots+p^{\frac{c-1}{2}}\right) \\ &=\left(1+p^{\frac{c+1}{2}}\right) * \operatorname{sum}\left(p, \frac{c-1}{2}\right) \end{aligned}

若 cc 为偶数, 类似地:

sum⁡(p,c)=(1+pc2)∗sum⁡(p,c2−1)+pc\operatorname{sum}(p, c)=\left(1+p^{\frac{c}{2}}\right) * \operatorname{sum}\left(p, \frac{c}{2}-1\right)+p^{c}

每次分治 (递归之后), 问题规模均会缩小一半, 配合快速幂即可在 O(log⁡c)\mathrm{O}(\log c) 的时间内求出等比数列的和。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
#include <vector>
#include <iostream>
#define ll long long
using namespace std;
const ll P = 9901;
vector<pair<ll, ll> > w;

ll ksm(ll a, ll b) {
	ll ans = 1;
	a %= P;
	while (b) {
		if (b & 1) (ans *= a) %= P;
		(a *= a) %= P;
		b >>= 1;
	}
	return ans;
}

ll get_sum(ll p, ll c) {
	if (!p) return 0;
	if (!c) return 1;
	if (c & 1) return (ksm(p, (c + 1) / 2) + 1) * get_sum(p, c / 2) % P;
	return ((ksm(p, c / 2) + 1) * get_sum(p, c / 2 - 1) + ksm(p, c)) % P;
}

void fj(ll a) {
	for (ll i = 2; i * i <= a; i++)
		if (!(a % i)) {
			ll num = 0;
			while (!(a % i)) {
				num++;
				a /= i;
			}
			w.push_back(make_pair(i, num));
		}
	if (a != 1) w.push_back(make_pair(a, 1));
}

int main() {
	ll a, b;
	cin >> a >> b;
	fj(a);
	ll ans = 1;
	for (unsigned ll i = 0; i < w.size(); i++) {
		ll p = w[i].first, c = w[i].second;
		(ans *= get_sum(p, b * c)) %= P;
	}
	cout << ans << endl;
	return 0;
}

Solution

分形

98. 分形之城

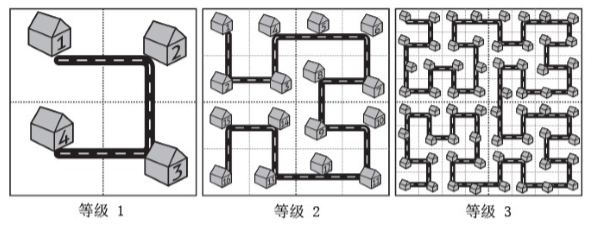
城市的规划在城市建设中是个大问题。

不幸的是，很多城市在开始建设的时候并没有很好的规划，城市规模扩大之后规划不合理的问题就开始显现。

而这座名为 Fractal 的城市设想了这样的一个规划方案，如下图所示：

当城区规模扩大之后，Fractal 的解决方案是把和原来城区结构一样的区域按照图中的方式建设在城市周围，提升城市的等级。

对于任意等级的城市，我们把正方形街区从左上角开始按照道路标号。

虽然这个方案很烂，Fractal 规划部门的人员还是想知道，如果城市发展到了等级 NN，编号为 AA 和 BB 的两个街区的直线距离是多少。

街区的距离指的是街区的中心点之间的距离，每个街区都是边长为 1010 米的正方形。

输入格式

第一行输入正整数 nn，表示测试数据的数目。

以下 nn 行，输入 nn 组测试数据，每组一行。

每组数据包括三个整数 N,A,BN, A, B，表示城市等级以及两个街区的编号，整数之间用空格隔开。

输出格式

一共输出 nn 行数据，每行对应一组测试数据的输出结果，结果四舍五入到整数。

数据范围

1≤N≤311 \le N \le 31,
1≤A,B≤22N1 \le A,B \le 2^{2N},
1≤n≤10001 \le n \le 1000

输入样例：

1
2
3
4
3 
1 1 2 
2 16 1 
3 4 33

输出样例：

1
2
3
10 
30 
50

算法分析

这就是著名的通过一定规律无限包含自身的 “分形” 图。为了计算方便, 我们把题目中房屋的编号都减去 1 , 即从 0 开始编号, 并把 SS 和 DD 也都减掉 1 。

本题关键是要解决：求编号为 MM 的房屋 (从 0 开始编号) 在 NN 级城市中的位置。把该问题记为 calc⁡(N,M)\operatorname{calc}(N, M), 本题就是求 calc⁡(N,S)\operatorname{calc}(N, S) 与 calc⁡(N,D)\operatorname{calc}(N, D) 的距离。

不难看出, N(N>1)N(N>1) 级城市由四座 N−1N-1 级城市组成, 其中左上的 N−1N-1 级城市顺时针旋转了 90 度，左下的 N−1N-1 级城市逆时针旋转了 90 度。进一步观察，当这四座 N−1N-1 级城市首尾相接后, 左上、左下的 N−1N-1 级城市的房屋编号顺序各自发生了颠倒, 这相当于左上、左下两座城市发生了“水平翻转”。

在求解 calc⁡(N,M)\operatorname{calc}(N, M) 时, 因为 N−1N-1 级城市有 22N−22^{2 N-2} 座房屋, 所以我们先递归求解 calc⁡(N−1,M mod 22N−2)\operatorname{calc}\left(N-1, M \bmod 2^{2 N-2}\right), 记求出的位置为 (x,y)(x, y), 其中 xx 为行号, yy 为列号, 从 0 开始编号。再根据 M/22N−2M / 2^{2 N-2} 的大小, 很容易确定编号为 MM 的房屋处于四座 N−1N-1 级城市中的哪一座。

  1. 若处于左上的 N−1N-1 级城市中, 则需要把 (x,y)(x, y) 所在的 N−1N-1 级城市顺时针旋转 90 度, 坐标变为 (y,2N−1−x−1)\left(y, 2^{N-1}-x-1\right), 再水平翻转, 坐标最终变为 (y,x)(y, x) 。这就是该房屋在 NN 级城市中的位置。
  2. 若处于右上的 N−1N-1 级城市中, 则该房屋在 NN 级城市中的位置应为 (x,y+(x, y+ 2N−1)\left.2^{N-1}\right) 。
  3. 若处于右下的 N−1N-1 级城市中, 则该房屋在 NN 级城市中的位置应为 (x+(x+ 2N−1,y+2N−1)\left.2^{N-1}, y+2^{N-1}\right) 。
  4. 若处于左下的 N−1N-1 级城市中, 则需要把 (x,y)(x, y) 所在的 N−1N-1 级城市逆时针旋转 90 度再水平翻转, 坐标变为 (2N−1−y−1,2N−1−x−1)\left(2^{N-1}-y-1,2^{N-1}-x-1\right) 。在 NN 级城市中的位置还要把行号再加 2N−12^{N-1}, 最终得到 (2N−y−1,2N−1−x−1)\left(2^{N}-y-1,2^{N-1}-x-1\right) 。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#include <cmath>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;

pair<long long, long long> calc(int n, long long m) {
    if (n == 0) return make_pair(0, 0);
    long long len = 1ll << (n - 1), cnt = 1ll << (2 * n - 2);
    pair<long long, long long> pos = calc(n - 1, m % cnt); // 递归
    long long x = pos.first, y = pos.second;
    long long z = m / cnt;
    if (z == 0) return make_pair(y, x);
    if (z == 1) return make_pair(x, y + len);
    if (z == 2) return make_pair(x + len, y + len);
    if (z == 3) return make_pair(2 * len - y - 1, len - x - 1);
}

int main () {
    int data; for (scanf("%d", &data); data; --data) {
        int n; long long h, o;
        scanf("%d %I64d %I64d", &n, &h, &o);
        pair<long long, long long> hp = calc(n, h - 1);
        pair<long long, long long> op = calc(n, o - 1);
        long long dx = hp.first - op.first, dy = hp.second - op.second;
        printf("%.0f\n", (double)sqrt(dx * dx + dy * dy) * 10);
    }
    return 0;
}

Solution

递归的机器实现

递归在计算机中是如何实现的? 换句话说, 它最终被编译成什么样的机器语言? 这就要从函数调用说起。实际上, 一台典型的 32 位计算机采用 “堆栈结构” 来实现函数调用, 它在汇编语言中, 把函数所需的第 kk 个, 第 k−1k-1 个, ⋯\cdots, 第 1 个参数依次入栈, 然后执行 call (address)指令。该指令把返回地址 (当前语句的下一条语句的地址) 入栈, 然后跳转到 address 位置的语句。在函数返回时, 它执行 ret 指令。该指令把返回地址出栈, 并跳转到该地址继续执行。

对于函数中定义的 C++局部变量, 在每次执行 call 与 ret 指令时, 也会在 “栈” 中相应地保存与复原, 而作用范围超过该函数的变量, 以及通过 new 和 malloc 函数动态分配的空间则保存在另一块称为 “堆” (注意, 这个堆与我们所说的二叉堆是两个不同的概念) 的结构中。栈指针、返回值、局部的运算会借助 CPU 的 “寄存器” 完成。

由此我们可以得知:

  1. 局部变量在每层递归中都占有一份空间, 声明过多或递归过深就会超过 “栈”所能存储的范围, 造成栈溢出。
  2. 非局部变量对于各层递归都共享同一份空间, 需要及时维护、还原现场, 以防止在各层递归之间存储和读取的数据互相影响。

了解了递归的机器实现之后, 我们就可以使用模拟的方法, 把递归程序改写为非递归程序。具体来说, 我们可以使用一个数组来模拟栈, 使用变量来模拟栈指针和返回值,使用 switch/case 或者 goto/label 来模拟语句跳转。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
// 模拟机器实现，把组合型枚举改为非递归
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>
using namespace std;
vector<int> chosen;
int stack[100010], top = 0, address = 0, n, m;
void call(int x, int ret_addr) { // 模拟计算机汇编指令call
	int old_top = top;
	stack[++top] = x; // 参数x
	stack[++top] = ret_addr; // 返回地址标号
	stack[++top] = old_top; // 在栈顶记录以前的top值
}
int ret() { // 模拟计算机汇编指令ret
	int ret_addr = stack[top - 1];
	top = stack[top]; // 恢复以前的top值
	return ret_addr;
}

int main() {
	cin >> n >> m;
	call(1, 0); // calc(1)
	while (top) {
		int x = stack[top - 2]; // 获取参数
		switch (address) {
		case 0:
			if (chosen.size()>m || chosen.size()+(n-x+1)<m) {
				address = ret(); // return
				continue;
			}
			if (x == n + 1) {
				for (int i = 0; i < chosen.size(); i++)
					printf("%d ", chosen[i]);
				puts("");
				address = ret(); // return
				continue;
			}
			chosen.push_back(x);
			call(x+1, 1); // 相当于calc(x+1)，返回后会从case 1继续
			address = 0;
			continue; // 回到while循环开头，相当于开始新的递归
		case 1:
			chosen.pop_back();
			call(x+1, 2); // 相当于calc(x+1)，返回后会从case 2继续
			address = 0;
			continue; // 回到while循环开头，相当于开始新的递归
		case 2:
			address = ret(); // 相当于原calc函数结尾，执行return
		}
	}
}