参考《算法竞赛进阶指南》、AcWing题库

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class BIT {
public:
    vector<int> c;
    int n;

    BIT() {}

    BIT(int n) {
        this->n = n;
        c.resize(n + 1);
    }

    BIT(vector<int> &a) {
        int n = a.size() + 1;
        c.resize(n);
        for (int i = 1; i <= n; ++i) {
            auto val = a[i - 1];
            c[i] += val;
            if (i + lowbit(i) <= n) c[i + lowbit(i)] += c[i]; 
        }
    }

    void add(int x, int w) {
        for (; x <= n; x += lowbit(x)) c[x] += w;
    }

    int askSum(int x) {
        int ans = 0;
        for (; x; x -= lowbit(x)) ans += c[x];
        return ans;
    }

    int lowbit(int x) {
        return x & -x;
    }
};

树状数组

在基本算法中, 我们详细探讨了位运算、二分、倍增等贯穿于各种数据结构设计始末的思想。无论是二进制、折半还是翻倍, 都与 “二” 这个数字密切相关。请读者回想倍增一文的 ST 表, 在对一个较大的连续线性范围进行统计时, 我们把它按照 2 的整数次幂分成若干个小范围进行预处理和计算。再回想位运算一文的快速幂算法, 根据任意正整数关于 2 的不重复次幂的唯一分解性质, 若一个正整数 xx 的二进制表示为 ak−1ak−2⋯a2a1a0a_{k-1} a_{k-2} \cdots a_{2} a_{1} a_{0}, 其中等于 1 的位是 {ai1,ai2,⋯ ,aim}\left\{a_{i_{1}}, a_{i_{2}}, \cdots, a_{i_{m}}\right\}, 则正整数 xx 可以被 “二进制分解” 成:

x=2i1+2i2+⋯+2imx=2^{i_{1}}+2^{i_{2}}+\cdots+2^{i_{m}}

不妨设 i1>i2>⋯>imi_{1}>i_{2}>\cdots>i_{m}, 进一步地, 区间 [1,x][1, x] 可以分成 O(log⁡x)O(\log x) 个小区间:

  1. 长度为 2i12^{i_{1}} 的小区间 [1,2i1]\left[1,2^{i_{1}}\right]
  2. 长度为 2i22^{i_{2}} 的小区间 [2i1+1,2i1+2i2]\left[2^{i_{1}}+1,2^{i_{1}}+2^{i_{2}}\right]
  3. 长度为 2i32^{i_{3}} 的小区间 [2i1+2i2+1,2i1+2i2+2i3]\left[2^{i_{1}}+2^{i_{2}}+1,2^{i_{1}}+2^{i_{2}}+2^{i_{3}}\right]
    …
    长度为 2im2^{i_{m}} 的小区间 [2i1+2i2+⋯+2im−1+1,2i1+2i2+⋯+2im]\left[2^{i_{1}}+2^{i_{2}}+\cdots+2^{i_{m-1}}+1,2^{i_{1}}+2^{i_{2}}+\cdots+2^{i_{m}}\right]

[x - lowbit(x) + 1, x] = (x - lowbit(x), x]

这些小区间的共同特点是：若区间结尾为 RR, 则区间长度就等于 RR 的 “二进制分解”下最小的 2 的次幕, 即 lowbit⁡(R)\operatorname{lowbit}(R) 。例如 x=7=22+21+20x=7=2^{2}+2^{1}+2^{0}, 区间 [1,7][1,7] 可以分成 [1,4]、[5,6][1,4] 、[5,6] 和 [7,7][7,7] 三个小区间, 长度分别是 lowbit⁡(4)=4、lowbit⁡(6)=2\operatorname{lowbit}(4)=4 、 \operatorname{lowbit}(6)=2 和 lowbit (7)=1(7)=1 。

我们在位运算 一文中探讨过 lowbit 运算, 并介绍了如何利用 lowbit 运算找出整数在 二进制表示下所有等于 1 的位。类似地, 给定一个整数 xx, 下面这段代码可以计算出区间 [1,x][1, x] 分成的 O(log⁡x)O(\log x) 个小区间:

1
2
3
while (x > 0) {
	printf("[%d, %d]\n", x - (x & -x) + 1, x);
}

树状数组结构

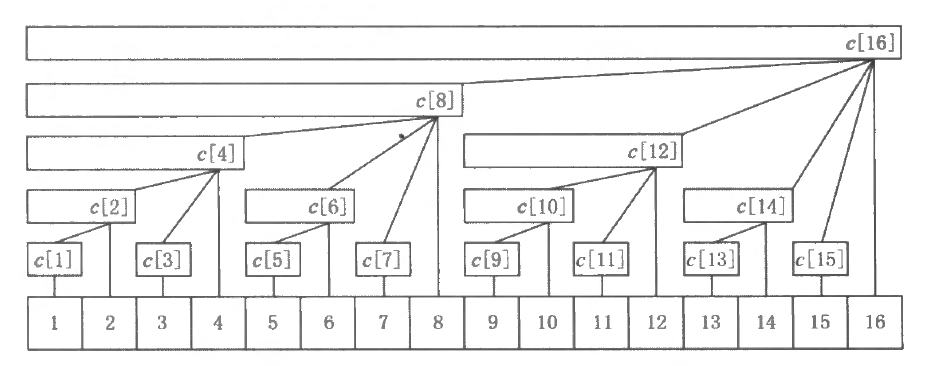
树状数组 (Binary Indexed Trees) 就是一种基于上述思想的数据结构, 其基本用途是维护序列的前缀和。对于给定的序列 aa, 我们建立一个数组 cc, 其中 c[x]c[x] 保存序列 aa 的区间 [x−lowbit⁡(x)+1,x][x-\operatorname{lowbit}(x)+1, x] 中所有数的和, 即 ∑i=x−lowbit⁡(x)+1xa[i]\sum_{i=x-\operatorname{lowbit}(x)+1}^{x} a[i] 。

事实上, 数组 cc 可以看作一个如下图所示的树形结构, 图中最下边一行是 NN 个叶节点 (N=16)(N=16), 代表数值 a[1∼N]a[1 \sim N] 。该结构满足以下性质:

  1. 每个内部节点 c[x]c[x] 保存以它为根的子树中所有叶节点的和。
  2. 每个内部节点 c[x]c[x] 的子节点个数等于 lowbit⁡(x)\operatorname{lowbit}(x) 的位数。
  3. 除树根外, 每个内部节点 c[x]c[x] 的父节点是 c[x+lowbit⁡(x)]c[x+\operatorname{lowbit}(x)] 。
  4. 树的深度为 O(log⁡N)\mathrm{O}(\log N) 。

如果 NN 不是 2 的整次幂, 那么树状数组就是一个具有同样性质的森林结构。

操作一：求前缀和

树状数组支持的基本操作有两个, 第一个操作是查询前缀和, 即序列 aa 第 1∼x1\sim x 个数的和。按照我们刚才提出的方法, 应该求出 xx 的二进制表示中每个等于 1 的位, 把 [1,x][1, x] 分成 O(log⁡N)O(\log N) 个小区间, 而每个小区间的区间和都已经保存在数组 cc 中。 所以, 把上面的代码稍加改写即可在 O(log⁡N)O(\log N) 的时间内查询前缀和:

1
2
3
4
5
int ask(int x) {
	int ans = 0;
	for (; x; x -= x & -x) ans += c[x];
	return ans;
}

当然, 若要查询序列 aa 的区间 [l,r][l, r] 中所有数的和, 只需计算 ask⁡(r)−ask⁡(l−1)\operatorname{ask}(r)-\operatorname{ask}(l- 1) 。

操作二：单点增加

树状数组支持的第二个基本操作是单点增加。意思是给序列中的一个数 a[x]a[x] 加上 yy, 同时正确维护序列的前缀和。根据上面给出的树形结构和它的性质, 只有节点 c[x]c[x] 及其所有祖先节点保存的 “区间和” 包含 a[x]a[x], 而任意一个节点的祖先至多只有 log⁡N\log N 个, 我们逐一对它们的 cc 值进行更新即可。下面的代码在 O(log⁡N)O(\log N) 时间内执行单点增加操作:

1
2
3
void add(int x, int y) {
	for (; x <= N; x += x & -x) c[x] += y;
}

树状数组初始化

在执行所有操作之前, 我们需要对树状数组进行初始化——针对原始序列 aa 构造一个树状数组。

为了简便, 比较一般的初始化方法是: 直接建立一个全为 0 的数组 cc, 然后对每个位置 xx 执行 add⁡(x,a[x])\operatorname{add}(x, a[x]), 就完成了对原始序列 aa 构造树状数组的过程, 时间复杂度为 O(Nlog⁡N)O(N \log N) 。通常采用这种初始化方法已经足够。

1
2
int c[N];
for (int i = 1; i <= n; ++i) add(i, a[i]);

更高效的初始化方法是: 从小到大依次考虑每个节点 xx, 借助 lowbit 运算扫描它的子节点并求和。若采用这种方法, 上面树形结构中的每条边只会被遍历一次, 时间复杂度为 O(∑k=1log⁡Nk∗N/2k)=O(N)O\left(\sum_{k=1}^{\log N} k * N / 2^{k}\right)=O(N) 。

1
2
3
4
5
int c[N];
for (int i = 1; i <= n; ++i) {
	c[i] += a[i];
	if (i + lowbit(i) <= n) c[i + lowbit(i)] += c[i];
}

还有一种简单的初始化方式：

  1. 先求前缀和sum数组
  2. c[x] = sum[x] - sum[x - lowbit(x)]

树状数组与逆序对

任意给定一个集合 aa, 如果用 t[val]t[v a l] 保存数值 valval 在集合 aa 中出现的次数, 那么数组 tt 在 [l,r][l, r] 上的区间和 (即 ∑i=lrt[i]\sum_{i=l}^{r} t[i] ) 就表示集合 aa 中范围在 [l,r][l, r] 内的数有多少个。

我们可以在集合 aa 的数值范围上建立一个树状数组, 来维护 tt 的前缀和。这样即使在集合 aa 中插入或删除一个数, 也可以高效地进行统计。

我们在排序一文中提到了逆序对问题以及使用归并排序的解法。对于一个序列 aa ，若 i<ji<j 且 a[i]>a[j]a[i]>a[j], 则称 a[i]a[i] 与 a[j]a[j] 构成逆序对。按照上述思路, 利用树状数组也可以求出一个序列的逆序对个数:

  1. 在序列 aa 的数值范围上建立树状数组, 初始化为全零。
  2. 倒序扫描给定的序列 aa, 对于每个数 a[i]a[i] :
    1. 在树状数组中查询前缀和 [1,a[i]−1][1, a[i]-1], 累加到答案 ansa n s 中。
    2. 执行 “单点增加” 操作, 即把位置 a[i]a[i] 上的数加 1 (相当于 t[a[i]]t[a[i]]++ ), 同时正确维护 tt 的前缀和。这表示数值 a[i]a[i] 又出现了 1 次。
  3. ans 即为所求。
1
2
3
4
for (int i = n; i; --i) {
	ans += ask(a[i] - 1);
	add(a[i], 1);
}

在这个算法中, 因为倒序扫描, “已经出现过的数” 就是在 a[i]a[i] 后边的数, 所以我们通过树状数组查询的内容就是 “每个 a[i]a[i] 后边有多少个比它小”。每次查询的结果之和当然就是逆序对个数。时间复杂度为 O((N+M)log⁡M),M\mathrm{O}((N+M) \log M), M 为数值范围的大小。

当数值范围较大时, 当然可以先进行离散化, 再用树状数组进行计算。不过因为离散化本身就要通过排序来实现, 所以在这种情况下就不如直接用归并排序来计算逆序对数了。

241. 楼兰图腾

在完成了分配任务之后，西部 314314 来到了楼兰古城的西部。

相传很久以前这片土地上(比楼兰古城还早)生活着两个部落，一个部落崇拜尖刀(V)，一个部落崇拜铁锹(∧)，他们分别用 V 和 ∧ 的形状来代表各自部落的图腾。

西部 314314 在楼兰古城的下面发现了一幅巨大的壁画，壁画上被标记出了 nn 个点，经测量发现这 nn 个点的水平位置和竖直位置是两两不同的。

西部 314314 认为这幅壁画所包含的信息与这 nn 个点的相对位置有关，因此不妨设坐标分别为 (1,y1),(2,y2),…,(n,yn)(1,y_1),(2,y_2),…,(n,y_n)，其中 y1∼yny_1 \sim y_n 是 11 到 nn 的一个排列。

西部 314314 打算研究这幅壁画中包含着多少个图腾。

如果三个点 (i,yi),(j,yj),(k,yk)(i,y_i),(j,y_j),(k,y_k) 满足 1≤i<j<k≤n1 \le i < j < k \le n 且 yi>yj,yj<yky_i > y_j, y_j < y_k，则称这三个点构成 V 图腾;

如果三个点 (i,yi),(j,yj),(k,yk)(i,y_i),(j,y_j),(k,y_k) 满足 1≤i<j<k≤n1 \le i < j< k \le n 且 yi<yj,yj>yky_i < y_j, y_j > y_k，则称这三个点构成 ∧ 图腾;

西部 314314 想知道，这 nn 个点中两个部落图腾的数目。

因此，你需要编写一个程序来求出 V 的个数和 ∧ 的个数。

输入格式

第一行一个数 nn。

第二行是 nn 个数，分别代表 y1，y2,…,yny_1，y_2,…,y_n。

输出格式

两个数，中间用空格隔开，依次为 V 的个数和 ∧ 的个数。

数据范围

对于所有数据，n≤200000n \le 200000，且输出答案不会超过 int64int64。
y1∼yny_1 \sim y_n 是 11 到 nn 的一个排列。

输入样例：

1
2
5
1 5 3 2 4

输出样例：

1
3 4

算法分析

题目描述的第一句话实际上告诉我们, 如果把这 NN 个点按照横坐标排序, 那么它们的纵坐标是 1∼N1 \sim N 的一个排列。我们把这个排列记为 aa 。

在树状数组求逆序对的算法中, 我们已经知道如何在一个序列中计算每个数后边有多少个数比它小。类似地, 我们可以:

  1. 倒序扫描序列 aa, 利用树状数组求出每个 a[i]a[i] 后边有几个数比它大, 记为 right[i]right[i] 。
  2. 正序扫描序列 aa, 利用树状数组求出每个 a[i]a[i] 前边有几个数比它大, 记为 left[i]left[i] 。

依次枚举每个点作为中间点, 以该点为中心的 “ v\mathrm{v} ” 字图腾个数显然是 left[i]∗right[i]left[i] * right[i] 。所以 “ v\mathrm{v} " 字图腾的总数就是 ∑i=1Nleft⁡[i]∗right⁡[i]\sum_{i=1}^{N} \operatorname{left}[i] * \operatorname{right}[i] 。按照同样的方法, 我们可以统计出 “^” 字图腾的个数。

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include <iostream>
#include <cstring>
using namespace std;

const int N = 2e5 + 10;

int n;
int a[N], c[N];
int l[N], r[N];

int ask(int x) {
    int ans = 0;
    for (; x; x -= x & -x) ans += c[x];
    return ans;
}

void add(int x, int w) {
    for (; x <= n; x += x & -x) c[x] += w;
}

int main() {
    cin >> n;
    for (int i = 1; i <= n; ++i) cin >> a[i];

    for (int i = n; i; --i) {
        int val = a[i];
        r[i] = ask(val - 1);
        add(val, 1);
    }
    
    memset(c, 0, sizeof c);
    for (int i = 1; i <= n; ++i) {
        int val = a[i];
        l[i] = ask(val - 1);
        add(val, 1);
    }
    
    long long ans1 = 0, ans2 = 0;
    for (int i = 1; i <= n; ++i) {
        ans1 += 1LL * (i - 1 - l[i]) * (n - i - r[i]);
        ans2 += 1LL * l[i] * r[i];
    }
    cout << ans1 << " " << ans2;
}

树状数组的扩展应用

（区间增加，单点查询）242. 一个简单的整数问题

给定长度为 NN 的数列 AA，然后输入 MM 行操作指令。

第一类指令形如 C l r d，表示把数列中第 l∼rl \sim r 个数都加 dd。

第二类指令形如 Q x，表示询问数列中第 xx 个数的值。

对于每个询问，输出一个整数表示答案。

输入格式

第一行包含两个整数 NN 和 MM。

第二行包含 NN 个整数 A[i]A[i]。

接下来 MM 行表示 MM 条指令，每条指令的格式如题目描述所示。

输出格式

对于每个询问，输出一个整数表示答案。

每个答案占一行。

数据范围

1≤N,M≤1051 \le N,M \le 10^5,
∣d∣≤10000|d| \le 10000,
∣A[i]∣≤109|A[i]| \le 10^9

输入样例：

1
2
3
4
5
6
7
10 5
1 2 3 4 5 6 7 8 9 10
Q 4
Q 1
Q 2
C 1 6 3
Q 2

输出样例：

1
2
3
4
4
1
2
5

算法分析

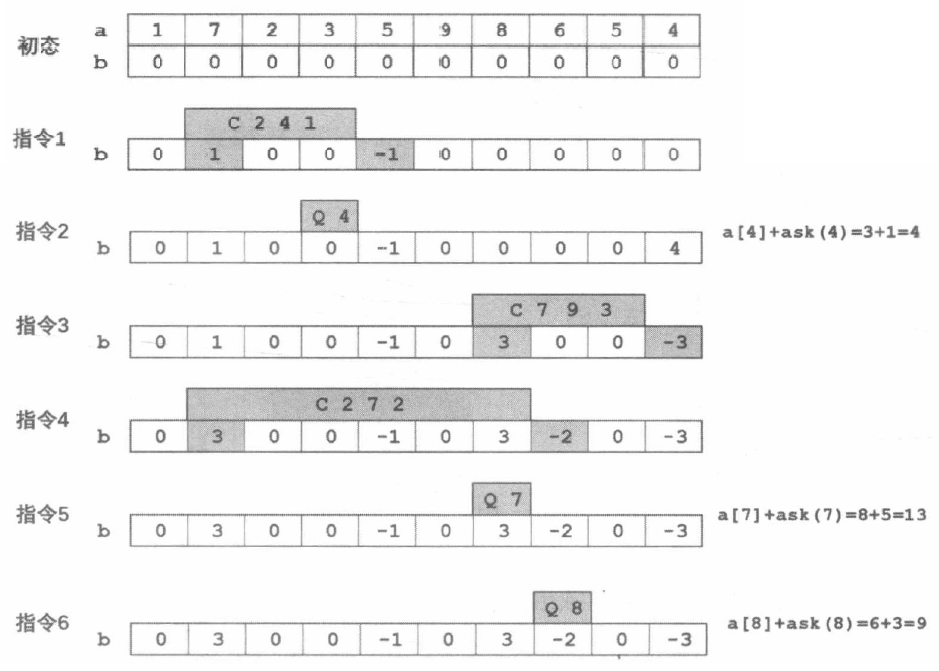
本题的指令有 “区间增加” 和 “单点查询”, 而树状数组仅支持 “单点增加” , 需要作出一些转化来解决问题。

新建一个数组 bb, 起初为全零。对于每条指令 “ C  l  r  d\mathrm{C} \;l \;\mathrm{r} \;d ", 我们把它转化成以下两 条指令:

  1. 把 b[l]b[l] 加上 dd 。
  2. 再把 b[r+1]b[r+1] 减去 dd 。

执行上面两条指令之后, 我们来考虑一下 bb 数组的前缀和 (b[1∼x]b[1 \sim x] 的和 ) 的情况：

  1. 对于 1≤x<l1 \leq x<l, 前缀和不变。
  2. 对于 l≤x≤rl \leq x \leq r, 前缀和增加了 dd 。
  3. 对于 r<x≤Nr<x \leq N, 前缀和不变 (l(l 处加 d,r+1d, r+1 处减 dd, 抵消)。

我们发现, bb 数组的前缀和 b[1∼x]b[1 \sim x] 就反映了指令 “ C  l  r  d\mathrm{C\;l\;r\;d} ” 对 a[x]a[x] 产生的影响。

于是, 我们可以用树状数组来维护数组 bb 的前缀和 (对 bb 只有单点增加操作)。因为各次操作之间具有可累加性, 所以在树状数组上查询前缀和 b[1∼x]b[1 \sim x], 就得出了到目前为止所有 “ C\mathrm{C} ” 指令在 a[x]a[x] 上增加的数值总和。再加上 a[x]a[x] 的初始值, 就得到了 “ Q  x\mathrm{Q} \;x ” 的答案。

该做法把 “维护数列的具体值” 转化为 “维护指令的累积影响”。每次修改的 “影响” 在 ll 处产生, 在 r+1r+1 处消除。 “影响” 的前缀和 b[1∼x]b[1 \sim x] 就代表了数值 a[x]a[x] 的变化情况, 如上图所示。该做法巧妙地把 “区间增加” + “单点查询” 变为树状数组擅长的 “单点增加” + “区间查询” 进行处理。

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#include <iostream>
using namespace std;
using LL = long long;

const int N = 1e5 + 10;

int n, m;
int a[N], c[N];

LL ask(int x) {
    LL ans = 0;
    for (; x; x -= x & -x) ans += c[x];
    return ans;
}

void add(int x, int w) {
    for (; x <= n; x += x & -x) c[x] += w;
}

int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; ++i) cin >> a[i];
    while (m--) {
        char op;
        cin >> op;
        if (op == 'Q') {
            int x; 
            cin >> x;
            cout << a[x] + ask(x) << endl;
        } else {
            int l, r, d;
            cin >> l >> r >> d;
            add(l, d);
            add(r + 1, -d);
        }
    }
}

（区间增加，区间和查询）243. 一个简单的整数问题2

给定一个长度为 NN 的数列 AA，以及 MM 条指令，每条指令可能是以下两种之一：

  1. C l r d，表示把 A[l],A[l+1],…,A[r]A[l],A[l+1],…,A[r] 都加上 dd。
  2. Q l r，表示询问数列中第 l∼rl \sim r 个数的和。

对于每个询问，输出一个整数表示答案。

输入格式

第一行两个整数 N,MN,M。

第二行 NN 个整数 A[i]A[i]。

接下来 MM 行表示 MM 条指令，每条指令的格式如题目描述所示。

输出格式

对于每个询问，输出一个整数表示答案。

每个答案占一行。

数据范围

1≤N,M≤1051 \le N,M \le 10^5,
∣d∣≤10000|d| \le 10000,
∣A[i]∣≤109|A[i]| \le 10^9

输入样例：

1
2
3
4
5
6
7
10 5
1 2 3 4 5 6 7 8 9 10
Q 4 4
Q 1 10
Q 2 4
C 3 6 3
Q 2 4

输出样例：

1
2
3
4
4
55
9
15

算法分析

在上一题中, 我们用树状数组维护了一个数组 bb, 对于每条指令 “ C  l  r  d\mathrm{C} \;l\; \mathrm{r} \;d ”, 把 b[l]b[l] 加上 dd, 再把 b[r+1]b[r+1] 减去 dd 。

我们已经讨论过, bb 数组的前缀和 ∑i=1xb[i]\sum_{i=1}^{x} b[i] 就是经过这些指令后 a[x]a[x] 增加的值。那么序列 aa 的前缀和 a[1∼x]a[1 \sim x] ，整体增加的值就是:

∑i=1x∑j=1ib[j]\sum_{i=1}^{x} \sum_{j=1}^{i} b[j]

上式可以改写为:

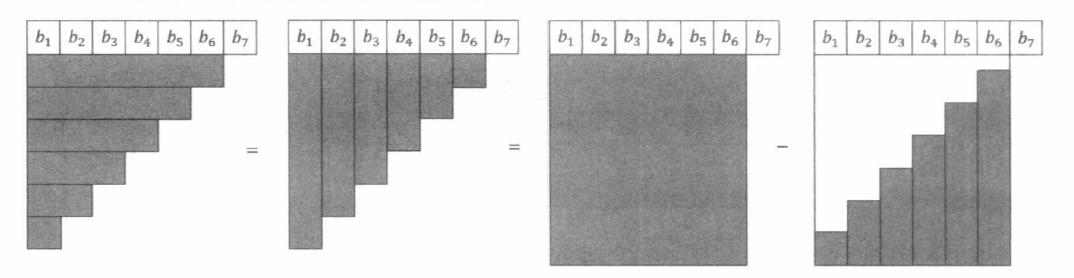
∑i=1x∑j=1ib[j]=∑i=1x(x−i+1)∗b[i]=(x+1)∑i=1xb[i]−∑i=1xi∗b[i]\sum_{i=1}^{x} \sum_{j=1}^{i} b[j]=\sum_{i=1}^{x}(x-i+1) * b[i]=(x+1) \sum_{i=1}^{x} b[i]-\sum_{i=1}^{x} i * b[i]

这个推导也可以用图形来直观描绘：

在本题中, 我们增加一个树状数组, 用于维护 i∗b[i]i * b[i] 的前缀和 ∑i=1xi∗b[i]\sum_{i=1}^{x} i * b[i], 上式就可以直接查询、计算了。

具体来说, 我们建立两个树状数组 c0c_{0} 和 c1c_{1}, 起初全部赋值为零。对于每条指令 “ Clrd⁡\operatorname{C l r d} ”, 执行 4 个操作:

  1. 在树状数组 c0c_{0} 中, 把位置 ll 上的数加 dd 。
  2. 在树状数组 c0c_{0} 中, 把位置 r+1r+1 上的数减 dd 。
  3. 在树状数组 c1c_{1} 中, 把位置 ll 上的数加 l∗dl * d 。
  4. 在树状数组 c1c_{1} 中, 把位置 r+1r+1 上的数减 (r+1)∗d(r+1) * d 。

另外, 我们建立数组 sum 存储序列 aa 的原始前缀和。对于每条指令 “ Q  l  rQ \;l\; r ”, 当然还是拆成 1∼r1 \sim r 和 1∼l−11 \sim l-1 两个部分, 二者相减。写成式子就是:

(sum[r]+(r+1)∗ask(c0,r)−ask(c1,r))  − (sum[r]+(r+1)*ask(c_{0}, r)-ask(c_{1}, r)) \;-

(sum[l−1]+l∗ask(c0,l−1)−ask(c1,l−1))(sum[l-1]+l * ask(c_{0}, l-1)-ask(c_{1}, l-1)) 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#include <iostream>
using namespace std;
using LL = long long;

const int N = 1e5 + 10;

int n, m;
int a[N];
LL sum[N], c[2][N];

LL ask(int k, int x) {
    LL ans = 0;
    for (; x; x -= x & -x) ans += c[k][x];
    return ans;
}

void add(int k, int x, LL w) {
    for (; x <= n; x += x & -x) c[k][x] += w;
}

LL prefixSum(int x) {
    return sum[x] + (x + 1) * ask(0, x) - ask(1, x);
} 

int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; ++i) cin >> a[i], sum[i] = sum[i - 1] + a[i];
    while (m--) {
        char op;
        int l, r;
        cin >> op >> l >> r;
        if (op == 'Q') {
            cout << prefixSum(r) - prefixSum(l - 1) << endl;
        } else {
            int d;
            cin >> d;
            add(0, l, d);
            add(0, r + 1, -d);
            add(1, l, l * d);
            add(1, r + 1, -(r + 1) * d);
        }
    }
}

值得指出的是, 为什么我们把 ∑i=1x(x−i+1)∗b[i]\sum_{i=1}^{x}(x-i+1) * b[i] 变成 (x+1)∑i=1xb[i]−∑i=1xi∗b[i](x+1) \sum_{i=1}^{x} b[i]-\sum_{i=1}^{x} i * b[i] 进行统计呢? 仔细观察该式的定义, 这里的 xx 是关于 “前缀和 a[1∼x]a[1 \sim x] ” 这个询问的变量, 而 ii 是在每次修改时影响的对象。

对于前者来说, 求和式中的每一项同时包含 xx 和 ii, 在修改时无法确定 (x−i+1)(x-i+1) 的值, 只能维护 b[i]b[i] 的前缀和。在询问时需要面临一个 “系数为等差数列” 的求和式, 计算起来非常困难。

对于后者来说, 求和式中的每一项只与 ii 有关。它通过一次容斥, 把 (x+1)(x+1) 提取为常量, 使得 b[i]b[i] 的前缀和与 i∗b[i]i * b[i] 的前缀和可以分别用树状数组进行维护。这种分离包含有多个变量的项, 使公式中不同变量之间互相独立的思想非常重要, 我们在讨论动态规划的优化策略时会多次用到。

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
#include <iostream>
using namespace std;
using LL = long long;

const int N = 1e5 + 10;

int n, m;
int a[N];
LL sum[N], c[2][N];

LL ask(int k, int x) {
    LL ans = 0;
    for (; x; x -= x & -x) ans += c[k][x];
    return ans;
}

void add(int k, int x, LL w) {
    for (; x <= n; x += x & -x) c[k][x] += w;
}

LL prefixSum(int x) {
    return (x + 1) * ask(0, x) - ask(1, x);
} 

int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; ++i) cin >> a[i];
    for (int i = 1; i <= n; ++i) {
        int b = a[i] - a[i - 1];
        add(0, i, b);
        add(1, i, 1LL * i * b);
    }
    while (m--) {
        char op;
        int l, r;
        cin >> op >> l >> r;
        if (op == 'Q') {
            cout << prefixSum(r) - prefixSum(l - 1) << endl;
        } else {
            int d;
            cin >> d;
            add(0, l, d);
            add(0, r + 1, -d);
            add(1, l, l * d);
            add(1, r + 1, -(r + 1) * d);
        }
    }
}

244. 谜一样的牛

有 nn 头奶牛，已知它们的身高为 1∼n1 \sim n 且各不相同，但不知道每头奶牛的具体身高。

现在这 nn 头奶牛站成一列，已知第 ii 头牛前面有 AiA_i 头牛比它低，求每头奶牛的身高。

输入格式

第 11 行：输入整数 nn。

第 2..n2..n 行：每行输入一个整数 AiA_i，第 ii 行表示第 ii 头牛前面有 AiA_i 头牛比它低。
（注意：因为第 11 头牛前面没有牛，所以并没有将它列出）

输出格式

输出包含 nn 行，每行输出一个整数表示牛的身高。

第 ii 行输出第 ii 头牛的身高。

数据范围

1≤n≤1051 \le n \le 10^5

输入样例：

1
2
3
4
5
5
1
2
1
0

输出样例：

1
2
3
4
5
2
4
5
3
1

算法分析

如果最后一头奶牛前面有 AnA_{n} 头牛比它低, 那么显然它的身高 Hn=An+1H_{n}=A_{n}+1 ，在所有牛中身高排第 An+1A_{n}+1 位。如果倒数第二头奶牛前有 An−1A_{n-1} 头牛比它低, 其在剩下的牛中的身高排第 An−1+1A_{n-1}+1 位，那么:

  1. 若 An−1<AnA_{n-1}<A_{n}, 则它的身高 Hn−1=An−1+1H_{n-1}=A_{n-1}+1 。
  2. 若 An−1≥AnA_{n-1} \geq A_{n}, 则它的身高 Hn−1=An−1+2H_{n-1}=A_{n-1}+2 。

依此类推, 如果第 kk 头牛前面有 AkA_{k} 头比它低, 那么它的身高 HkH_{k} 是数值 1∼n1 \sim n 中第 Ak+1A_{k}+1 小的没有在 {Hk+1,Hk+2,⋯ ,Hn}\left\{H_{k+1}, H_{k+2}, \cdots, H_{n}\right\} 中出现过的数。

核心问题：

  1. 从剩余数中，找出第 kk 小的数
  2. 删除某个数

具体来说, 我们建立一个长度为 nn 的 01 序列 bb, 起初全部为 1 ，b[i] = 1 表示身高 i 可用。然后, 从 nn 到 1 倒序扫描每个 AiA_{i}, 对每个 AiA_{i} 执行以下两个操作:

  1. 查询序列 bb 中第 Ai+1A_{i}+1 个 1 在什么位置, 这个位置号就是第 ii 头奶牛的身高 HiH_{i} 。
  2. 把 b[Hi]b\left[H_{i}\right] 减 1 (从 1 变为 0)) 。

也就是说, 我们需要实时维护一个 01 序列, 支持查询第 kk 个 1 的位置 (k(k 为任意整数), 以及修改序列中的一个数值。

方法一: 树状数组+二分, 单次操作 O(log⁡2n)O\left(\log ^{2} n\right)

用树状数组 cc 维护 01 序列 bb 的前缀和, 在每次查询时二分答案, 通过 ask⁡(mid)\operatorname{ask}(\mathrm{mid}) 即可得到前 mid 个数中有多少个 1, 与 kk 比较大小, 即可确定二分上下界的变化。

方法二: 树状数组+倍增, 单次操作 O(log⁡n)O(\log n)

用树状数组 cc 维护 01 序列 bb 的前缀和, 在每次查询时:

  1. 初始化两个变量 ans=0a n s=0 和 sum=0s u m=0 。
  2. 从 log⁡n\log n (下取整) 到 0 倒序考虑每个整数 pp 。
    对于每个 pp, 若 ans+2p≤na n s+2^{p} \leq n 且 sum+c[ans+2p]<ks u m+c\left[a n s+2^{p}\right]<k, 则令 sum+=c[ans+2p]  ,  ans+=2ps u m+=c[a n s+2^{p}]\;,\;ans+=2^{p} 。
  3. 最后, Hi=ans+1H_{i}=a n s+1 即为所求。

该做法与 “倍增” 中给出的第一个小问题采用了类似的思想, 都是 “以 2 的整数次幂为步长, 能累加则累加”。树状数组 cc 恰好已经为我们维护了区间长度为 2 的次幂的一些信息, 直接结合树状数组使用这种思想, 就得到了上面这个高效算法。

Solution

树状数组 + 二分
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include <iostream>
using namespace std;

const int N = 1e5 + 10;

int n;
int h[N], c[N], ans[N];

void add(int x, int w) {
    for (; x <= n; x += x & -x) c[x] += w;
}

int ask(int x) {
    int ans = 0;
    for (; x; x -= x & -x) ans += c[x];
    return ans;
}

int main() {
    cin >> n;
    for (int i = 2; i <= n; ++i) cin >> h[i];
    
    for (int i = 1; i <= n; ++i) add(i, 1);
    
    for (int i = n; i; --i) {
        int k = h[i] + 1;
        int l = 1, r = n;
        while (l < r) {
            int mid = l + r >> 1;
            if (ask(mid) >= k) r = mid;
            else l = mid + 1;
        }
        ans[i] = r;
        add(r, -1);
    }
    
    for (int i = 1; i <= n; ++i) cout << ans[i] << endl;
}