参考《算法竞赛进阶指南》 、AcWing题库
树的直径与最近公共祖先
树的直径
给定一棵树, 树中每条边都有一个权值, 树中两点之间的距离定义为连接两点的路径上的边权之和。树中最远的两个节点之间的距离被称为树的直径 , 连接这两点的路径被称为树的最长链 。后者通常也可称为直径, 即直径既是一个数值概念, 也可代指一条 路径。
树的直径一般有两种求法, 时间复杂度都是 O ( N ) O(N) O ( N ) N N N N − 1 N-1 N − 1
树形 DP 求树的直径
不妨设 1 号节点为根, “ N N N N − 1 N-1 N − 1
设 D [ x ] D[x] D [ x ] x x x x x x x x x y 1 , y 2 , ⋯ , y t y_{1}, y_{2}, \cdots, y_{t} y 1 , y 2 , ⋯ , y t e d g e ( x , y ) edge(x, y) e d g e ( x , y )
D [ x ] = max 1 ≤ i ≤ t { D [ y i ] + edge ( x , y i ) } D[x]=\max _{1 \leq i \leq t}\left\{D\left[y_{i}\right]+\operatorname{edge}\left(x, y_{i}\right)\right\}
D [ x ] = 1 ≤ i ≤ t max { D [ y i ] + edge ( x , y i ) }
接下来, 我们可以考虑对每个节点 x x x x x x F [ x ] F[x] F [ x ] max 1 ≤ x ≤ n { F [ x ] } \max _{1 \leq x \leq n}\{F[x]\} max 1 ≤ x ≤ n { F [ x ]}
那么如何求出 F [ x ] F[x] F [ x ] x x x y i y_{i} y i y j y_{j} y j x x x y i y_{i} y i y i y_{i} y i ( x , y i ) \left(x, y_{i}\right) ( x , y i ) ( x , y j ) \left(x, y_{j}\right) ( x , y j ) y j y_{j} y j y j y_{j} y j j < i j<i j < i
F [ x ] = max 1 ≤ j < i ≤ t { D [ y i ] + D [ y j ] + edge ( x , y i ) + edge ( x , y j ) } F[x]=\max _{1 \leq j<i \leq t}\left\{D\left[y_{i}\right]+D\left[y_{j}\right]+\operatorname{edge}\left(x, y_{i}\right)+\operatorname{edge}\left(x, y_{j}\right)\right\}
F [ x ] = 1 ≤ j < i ≤ t max { D [ y i ] + D [ y j ] + edge ( x , y i ) + edge ( x , y j ) }
我们没有必要使用两层循环来枚举 i , j i, j i , j D [ x ] D[x] D [ x ] i i i D [ x ] D[x] D [ x ] x x x y j ( j < i ) y_{j}(j<i) y j ( j < i ) max 1 ≤ j < i { D [ y j ] + edge ( x , y j ) } \max _{1 \leq j<i}\left\{D\left[y_{j}\right]+\operatorname{edge}\left(x, y_{j}\right)\right\} max 1 ≤ j < i { D [ y j ] + edge ( x , y j ) } D [ x ] + D [ y i ] + edge ( x , y i ) D[x]+D\left[y_{i}\right]+\operatorname{edge}\left(x, y_{i}\right) D [ x ] + D [ y i ] + edge ( x , y i ) F [ x ] F[x] F [ x ] D [ y i ] + edge ( x , y i ) D\left[y_{i}\right]+\operatorname{edge}\left(x, y_{i}\right) D [ y i ] + edge ( x , y i ) D [ x ] D[x] D [ x ]
1 2 3 4 5 6 7 8 9 10 11 void dp (int x) v[x] = 1 ; for (int i = head[x]; i; i = Next[i]) { int y = ver[i]; if (v[y]) continue ; dp (y); ans = max (ans, d[x] + d[y] + edge[i]); d[x] = max (d[x], d[y] + edge[i]); } }
两次 BFS 求树的直径
通过两次 BFS 或者两次 DFS 也可以求出树的直径, 并且更容易计算出直径上的具体节点。详细地说, 这种做法包括两步:
从任意一个节点出发, 通过 BFS 或 DFS 对树进行一次遍历, 求出与出发点距离最远的节点, 记为 p p p
从节点 p p p p p p q q q
从 p p p q q q p p p p p p p p p q q q q q q p p p
树的直径可以作为很多树上问题的突破口。接下来我们给出两道例题。除此之外, 读者还将在图论总结与练习中解决树的直径的必须边等问题。
在一个地区有 n n n 1 , 2 , … , n 1,2,…,n 1 , 2 , … , n
有 n − 1 n-1 n − 1
每条道路的长度均为 1 1 1
为保证该地区的安全,巡警车每天都要到所有的道路上巡逻。
警察局设在编号为 1 1 1
为了减少总的巡逻距离,该地区准备在这些村庄之间建立 K K K
两条新道路可以在同一个村庄会合或结束,甚至新道路可以是一个环。
因为资金有限,所以 K K K 1 1 1 2 2 2
同时,为了不浪费资金,每天巡警车必须经过新建的道路正好一次。
编写一个程序,在给定村庄间道路信息和需要新建的道路数的情况下,计算出最佳的新建道路的方案,使得总的巡逻距离最小。
输入格式
第一行包含两个整数 n n n K K K
接下来 n − 1 n-1 n − 1 a a a b b b a a a b b b
输出格式
输出一个整数,表示新建了 K K K
数据范围
3 ≤ n ≤ 100000 3 \le n \le 100000 3 ≤ n ≤ 100000 1 ≤ K ≤ 2 1 \le K \le 2 1 ≤ K ≤ 2 1 ≤ a , b ≤ n 1 \le a,b \le n 1 ≤ a , b ≤ n
输入样例:
1 2 3 4 5 6 7 8 8 1 1 2 3 1 3 4 5 3 7 5 8 5 5 6
输出样例:
算法分析
Solution
设 T = ( V , E , W ) T=(V, E, W) T = ( V , E , W ) T T T V , E V, E V , E W W W T T T n n n
路径:树网中任何两结点 a , b a,b a , b d ( a , b ) d(a,b) d ( a , b ) a , b a,b a , b
我们称 d ( a , b ) d(a,b) d ( a , b ) a , b a,b a , b
一点 v v v P P P P P P
d ( v , P ) = m i n { d ( v , u ) } d(v,P)=min\{d(v,u)\} d ( v , P ) = min { d ( v , u )} u u u P P P
树网的直径:树网中最长的路径称为树网的直径。
对于给定的树网 T T T
偏心距 E C C ( F ) ECC(F) ECC ( F ) T T T F F F F F F
E C C ( F ) = m a x { d ( v , F ) , v ∈ V } ECC(F)=max\{d(v,F),v∈V\} ECC ( F ) = ma x { d ( v , F ) , v ∈ V }
任务:对于给定的树网 T = ( V , E , W ) T=(V, E,W) T = ( V , E , W ) s s s F F F s s s s s s E C C ( F ) ECC(F) ECC ( F )
我们称这个路径为树网 T = ( V , E , W ) T=(V,E,W) T = ( V , E , W )
必要时,F F F
一般来说,在上述定义下,核不一定只有一个,但最小偏心距是唯一的。
输入格式
包含 n n n 1 1 1 n n n s s s n n n s s s 1 , 2 , … , n 1, 2, …, n 1 , 2 , … , n
从第 2 2 2 n n n 3 3 3
例如,2 4 7 表示连接结点 2 2 2 4 4 4 7 7 7
所给的数据都是正确的,不必检验。
输出格式
只有一个非负整数,为指定意义下的最小偏心距。
数据范围
n ≤ 500000 , s < 2 31 n \le 500000,s < 2^{31} n ≤ 500000 , s < 2 31
输入样例:
1 2 3 4 5 5 2 1 2 5 2 3 2 2 4 4 2 5 3
输出样例:
算法分析
Solution
最近公共祖先(LCA)
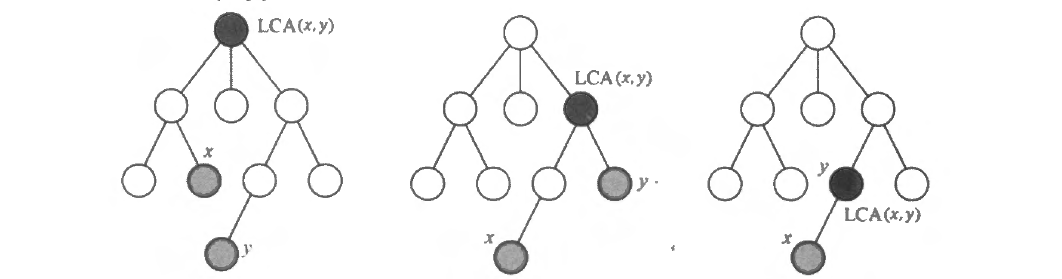
给定一棵有根树, 若节点 z z z x x x y y y z z z x , y x, y x , y x , y x, y x , y x , y x, y x , y ( x , y ) (x, y) ( x , y )
LCA ( x , y ) \operatorname{LCA}(x, y) LCA ( x , y ) x x x y y y x x x y y y
向上标记法
从 x x x y y y LCA ( x , y ) \operatorname{LCA}(x, y) LCA ( x , y ) O ( n ) O(n) O ( n )
树上倍增法
树上倍增法是一个很重要的算法。除了求 LCA 之外, 它在很多问题中都有广泛应用。设 F [ x , k ] F[x, k] F [ x , k ] x x x 2 k 2^{k} 2 k x x x 2 k 2^{k} 2 k F [ x , k ] = 0 F[x, k]=0 F [ x , k ] = 0 F [ x , 0 ] F[x, 0] F [ x , 0 ] x x x ∀ k ∈ [ 1 , log n ] \forall k \in [1, \log n] ∀ k ∈ [ 1 , log n ] F [ x , k ] = F [ F [ x , k − 1 ] , k − 1 ] F[x, k]=F[F[x, k-1], k-1] F [ x , k ] = F [ F [ x , k − 1 ] , k − 1 ]
这类似于一个动态规划的过程, “阶段” 就是节点的深度。因此, 我们可以对树进行广度优先遍历, 按照层次顺序, 在节点入队之前, 计算它在 F F F
以上部分是预处理, 时间复杂度为 O ( n log n ) O(n \log n) O ( n log n ) x , y x, y x , y O ( log n ) O(\log n) O ( log n )
基于 F F F LCA ( x , y ) \operatorname{LCA}(x, y) LCA ( x , y )
设 d [ x ] d[x] d [ x ] x x x d [ x ] ≥ d [ y ] d[x] \geq d[y] d [ x ] ≥ d [ y ] x , y x, y x , y
用二进制拆分思想, 把 x x x y y y x x x k = 2 log n , ⋯ , 2 1 , 2 0 k=2^{\log n}, \cdots, 2^{1}, 2^{0} k = 2 l o g n , ⋯ , 2 1 , 2 0 y y y x = F [ x , k ] x=F[x, k] x = F [ x , k ]
若此时 x = y x=y x = y y y y
用二进制拆分思想, 把 x , y x, y x , y x , y x, y x , y k = 2 log n , ⋯ , 2 1 , 2 0 k=2^{\log n}, \cdots, 2^{1}, 2^{0} k = 2 l o g n , ⋯ , 2 1 , 2 0 F [ x , k ] ≠ F [ y , k ] F[x, k] \neq F[y, k] F [ x , k ] = F [ y , k ] x = F [ x , k ] , y = F [ y , k ] x=F[x, k], y=F[y, k] x = F [ x , k ] , y = F [ y , k ]
此时 x , y x, y x , y F [ x , 0 ] F[x, 0] F [ x , 0 ]
请读者画图理解, 并参阅下面的程序。程序以模板题 HDOJ2586 “How far away?” 为例, 多次查询树上两点之间的距离, 时间复杂度为 O ( ( n + m ) log n ) \mathrm{O}((n+m) \log n) O (( n + m ) log n )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 #include <iostream> #include <cstdio> #include <cstring> #include <algorithm> #include <queue> #include <cmath> using namespace std;const int SIZE = 50010 ;int f[SIZE][20 ], d[SIZE], dist[SIZE];int ver[2 * SIZE], Next[2 * SIZE], edge[2 * SIZE], head[SIZE];int T, n, m, tot, t;queue<int > q; void add (int x, int y, int z) ver[++tot] = y; edge[tot] = z; Next[tot] = head[x]; head[x] = tot; } void bfs () q.push (1 ); d[1 ] = 1 ; while (q.size ()) { int x = q.front (); q.pop (); for (int i = head[x]; i; i = Next[i]) { int y = ver[i]; if (d[y]) continue ; d[y] = d[x] + 1 ; dist[y] = dist[x] + edge[i]; f[y][0 ] = x; for (int j = 1 ; j <= t; j++) f[y][j] = f[f[y][j - 1 ]][j - 1 ]; q.push (y); } } } int lca (int x, int y) if (d[x] > d[y]) swap (x, y); for (int i = t; i >= 0 ; i--) if (d[f[y][i]] >= d[x]) y = f[y][i]; if (x == y) return x; for (int i = t; i >= 0 ; i--) if (f[x][i] != f[y][i]) x = f[x][i], y = f[y][i]; return f[x][0 ]; } int main () cin >> T; while (T--) { cin >> n >> m; t = (int )(log (n) / log (2 )) + 1 ; for (int i = 1 ; i <= n; i++) head[i] = d[i] = 0 ; tot = 0 ; for (int i = 1 ; i < n; i++) { int x, y, z; scanf ("%d%d%d" , &x, &y, &z); add (x, y, z), add (y, x, z); } bfs (); for (int i = 1 ; i <= m; i++) { int x, y; scanf ("%d%d" , &x, &y); printf ("%d\n" , dist[x] + dist[y] - 2 * dist[lca (x, y)]); } } }
LCA 的 Tarjan 算法
Tarjan 算法本质上是使用并查集对 “向上标记法” 的优化。它是一个离线算法, 需要把 m m m O ( n + m ) \mathrm{O}(n+m) O ( n + m )
在深度优先遍历的任意时刻, 树中节点分为三类:
已经访问完毕并且回溯的节点。在这些节点上标记一个整数 2。
已经开始递归, 但尚未回溯的节点。这些节点就是当前正在访问的节点 x x x x x x
尚未访问的节点。这些节点没有标记。
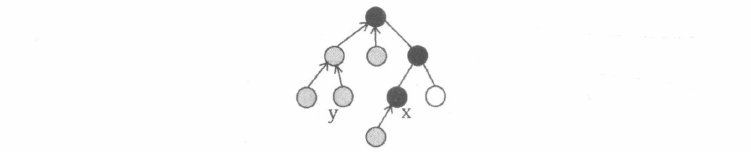
对于正在访问的节点 x x x y y y LCA ( x , y ) \operatorname{LCA}(x, y) LCA ( x , y ) y y y
可以利用并查集进行优化, 当一个节点获得整数 2 的标记时, 把它所在的集合合并到它的父节点所在的集合中(合并时它的父节点标记一定为 1, 且单独构成一个集合)。
这相当于每个完成回溯的节点都有一个指针指向它的父节点, 只需查询 y y y y y y LCA ( x , y ) \operatorname{LCA}(x, y) LCA ( x , y )
在 x x x
此时扫描与 x x x y y y y y y
下面的参考程序以模板题 HDOJ2586 “How far away?” 为例, 多次查询树上两点之间的距离, 时间复杂度为 O ( n + m ) O(n+m) O ( n + m )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 #include <iostream> #include <cstdio> #include <cstring> #include <algorithm> #include <vector> using namespace std;const int SIZE = 50010 ;int ver[2 * SIZE], Next[2 * SIZE], edge[2 * SIZE], head[SIZE];int fa[SIZE], d[SIZE], v[SIZE], lca[SIZE], ans[SIZE];vector<int > query[SIZE], query_id[SIZE]; int T, n, m, tot, t;void add (int x, int y, int z) ver[++tot] = y; edge[tot] = z; Next[tot] = head[x]; head[x] = tot; } void add_query (int x, int y, int id) query[x].push_back (y), query_id[x].push_back (id); query[y].push_back (x), query_id[y].push_back (id); } int get (int x) if (x == fa[x]) return x; return fa[x] = get (fa[x]); } void tarjan (int x) v[x] = 1 ; for (int i = head[x]; i; i = Next[i]) { int y = ver[i]; if (v[y]) continue ; d[y] = d[x] + edge[i]; tarjan (y); fa[y] = x; } for (int i = 0 ; i < query[x].size (); i++) { int y = query[x][i]; int id = query_id[x][i]; if (v[y] == 2 ) { int lca = get (y); ans[id] = min (ans[id], d[x] + d[y] - 2 * d[lca]); } } v[x] = 2 ; } int main () cin >> T; while (T--) { cin >> n >> m; for (int i = 1 ; i <= n; i++) { head[i] = 0 ; query[i].clear (), query_id[i].clear (); fa[i] = i, v[i] = 0 ; } tot = 0 ; for (int i = 1 ; i < n; i++) { int x, y, z; scanf ("%d%d%d" , &x, &y, &z); add (x, y, z), add (y, x, z); } for (int i = 1 ; i <= m; i++) { int x, y; scanf ("%d%d" , &x, &y); if (x == y) ans[i] = 0 ; else { add_query (x, y, i); ans[i] = 1 << 30 ; } } tarjan (1 ); for (int i = 1 ; i <= m; i++) printf ("%d\n" , ans[i]); } }
树上差分
在 “前缀和与差分” 中, 我们定义了一个序列的前缀和与差分序列, 并通过差分技巧, 把 “区间” 的增减转化为 “左端点加 1 , 右端点减 1 ”。根据 “差分序列的前缀和是原序列” 这一原理, 在树上可以进行类似的简化, 其中 “区间操作” 对应为 “路径操作”, “前缀和” 对应为 “子树和”。我们通过具体的例子来详细探讨。
传说中的暗之连锁被人们称为 Dark。
Dark 是人类内心的黑暗的产物,古今中外的勇者们都试图打倒它。
经过研究,你发现 Dark 呈现无向图的结构,图中有 N N N
Dark 有 N – 1 N – 1 N –1
另外,Dark 还有 M M M
你的任务是把 Dark 斩为不连通的两部分。
一开始 Dark 的附加边都处于无敌状态,你只能选择一条主要边切断。
一旦你切断了一条主要边,Dark 就会进入防御模式,主要边会变为无敌的而附加边可以被切断。
但是你的能力只能再切断 Dark 的一条附加边。
现在你想要知道,一共有多少种方案可以击败 Dark。
注意,就算你第一步切断主要边之后就已经把 Dark 斩为两截,你也需要切断一条附加边才算击败了 Dark。
输入格式
第一行包含两个整数 N N N M M M
之后 N – 1 N – 1 N –1 A A A B B B A A A B B B
之后 M M M
输出格式
输出一个整数表示答案。
数据范围
N ≤ 100000 , M ≤ 200000 N \le 100000,M \le 200000 N ≤ 100000 , M ≤ 200000 2 31 − 1 2^{31}-1 2 31 − 1
输入样例:
输出样例:
算法分析
Solution
深绘里一直很讨厌雨天。
灼热的天气穿透了前半个夏天,后来一场大雨和随之而来的洪水,浇灭了一切。
虽然深绘里家乡的小村落对洪水有着顽固的抵抗力,但也倒了几座老房子,几棵老树被连根拔起,以及田地里的粮食被弄得一片狼藉。
无奈的深绘里和村民们只好等待救济粮来维生。
不过救济粮的发放方式很特别。
有 n n n
有 m m m x , y x,y x , y x x x y y y x , y x,y x , y z z z
求完成所有发放操作后,每个点存放最多的是哪种类型的物品。
输入格式
第一行两个正整数 n , m n,m n , m
接下来 n − 1 n-1 n − 1 ( a , b ) (a,b) ( a , b ) ( a , b ) (a,b) ( a , b )
再接下来 m m m ( x , y , z ) (x,y,z) ( x , y , z )
输出格式
共 n n n i i i i i i
如果某座房屋里没有救济粮,则对应一行输出 0 0 0
数据范围
1 ≤ n , m ≤ 100000 1 \le n,m \le 100000 1 ≤ n , m ≤ 100000 1 ≤ z ≤ 1 0 5 1 \le z \le 10^5 1 ≤ z ≤ 1 0 5
输入样例:
1 2 3 4 5 6 7 8 5 3 1 2 3 1 3 4 5 3 2 3 3 1 5 2 3 3 3
输出样例:
算法分析
Solution
小 C C C
《天天爱跑步》是一个养成类游戏,需要玩家每天按时上线,完成打卡任务。
这个游戏的地图可以看作一棵包含 n n n n − 1 n-1 n − 1
树上节点的编号是 1 ∼ n 1 \sim n 1 ∼ n
现在有 m m m i i i S i S_i S i T i T_i T i
每天打卡任务开始时,所有玩家在第 0 0 0
因为地图是一棵树,所以每个人的路径是唯一的。
小 C C C
在节点 j j j W j W_j W j W j W_j W j j j j
小 C C C
注意:我们认为一个玩家到达自己的终点后,该玩家就会结束游戏,他不能等待一段时间后再被观察员观察到。
即对于把节点 j j j W j W_j W j j j j W j W_j W j j j j
输入格式
第一行有两个整数 n n n m m m
其中 n n n m m m
接下来 n − 1 n-1 n − 1 U U U V V V U U U V V V
接下来一行 n n n W j W_j W j
接下来 m m m S i S_i S i T i T_i T i
输出格式
一行 n n n i i i i i i
数据范围
1 ≤ n , m ≤ 3 × 1 0 5 1 \le n,m \le 3 \times 10^5 1 ≤ n , m ≤ 3 × 1 0 5
输入样例:
1 2 3 4 5 6 7 8 9 10 6 3 2 3 1 2 1 4 4 5 4 6 0 2 5 1 2 3 1 5 1 3 2 6
输出样例:
算法分析
Solution
LCA 的综合应用
Adera 是 Microsoft 应用商店中的一款解谜游戏。
异象石是进入 Adera 中异时空的引导物,在 Adera 的异时空中有一张地图。
这张地图上有 N N N N − 1 N-1 N − 1
起初地图上没有任何异象石,在接下来的 M M M
地图的某个点上出现了异象石(已经出现的不会再次出现);
地图某个点上的异象石被摧毁(不会摧毁没有异象石的点);
向玩家询问使所有异象石所在的点连通的边集的总长度最小是多少。
请你作为玩家回答这些问题。
输入格式
第一行有一个整数 N N N
接下来 N − 1 N-1 N − 1 x , y , z x,y,z x , y , z x x x y y y z z z
第 N + 1 N+1 N + 1 M M M
接下来 M M M
+ x 表示点 x x x - x 表示点 x x x ? 表示询问使当前所有异象石所在的点连通所需的边集的总长度最小是多少。
输出格式
对于每个 ? 事件,输出一个整数表示答案。
数据范围
1 ≤ N , M ≤ 1 0 5 1 \le N,M \le 10^5 1 ≤ N , M ≤ 1 0 5 1 ≤ x , y ≤ N 1 \le x,y \le N 1 ≤ x , y ≤ N x ≠ y x \neq y x = y 1 ≤ z ≤ 1 0 9 1 \le z \le 10^9 1 ≤ z ≤ 1 0 9
输入样例:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 6 1 2 1 1 3 5 4 1 7 4 5 3 6 4 2 10 + 3 + 1 ? + 6 ? + 5 ? - 6 - 3 ?
输出样例:
算法分析
Solution
给定一张 N N N M M M
设最小生成树的边权之和为 s u m sum s u m s u m sum s u m
输入格式
第一行包含两个整数 N N N M M M
接下来 M M M x , y , z x,y,z x , y , z x x x y y y z z z
输出格式
包含一行,仅一个数,表示严格次小生成树的边权和。(数据保证必定存在严格次小生成树)
数据范围
N ≤ 1 0 5 , M ≤ 3 × 1 0 5 N \le 10^5,M \le 3 \times 10^5 N ≤ 1 0 5 , M ≤ 3 × 1 0 5
输入样例:
1 2 3 4 5 6 7 5 6 1 2 1 1 3 2 2 4 3 3 5 4 3 4 3 4 5 6
输出样例:
算法分析
Solution
H H H n n n n n n n − 1 n-1 n − 1 1 1 1
H H H
当局为了控制疫情,不让疫情扩散到边境城市(叶子节点所表示的城市),决定动用军队在一些城市建立检查点,使得从首都到边境城市的每一条路径上都至少有一个检查点,边境城市也可以建立检查点。
但要注意的是,首都是不能建立检查点的。
现在,在 H H H
军队总数为 m m m
一支军队可以在有道路连接的城市间移动,并在除首都以外的任意一个城市建立检查点,且只能在一个城市建立检查点。
一支军队经过一条道路从一个城市移动到另一个城市所需要的时间等于道路的长度(单位:小时)。
请问:最少需要多少个小时才能控制疫情?
注意:不同的军队可以同时移动。
输入格式
第一行一个整数 n n n
接下来的 n − 1 n-1 n − 1 3 3 3 u 、 v 、 w u、v、w u 、 v 、 w u u u v v v w w w 1 1 1
接下来一行一个整数 m m m
接下来一行 m m m m m m
输出格式
共一行,包含一个整数,表示控制疫情所需要的最少时间。如果无法控制疫情则输出 − 1 -1 − 1
数据范围
2 ≤ m ≤ n ≤ 50000 2 \le m \le n \le 50000 2 ≤ m ≤ n ≤ 50000 0 < w < 1 0 9 0 < w < 10^9 0 < w < 1 0 9
输入样例:
1 2 3 4 5 6 4 1 2 1 1 3 2 3 4 3 2 2 2
输出样例:
算法分析
Solution