参考《算法竞赛进阶指南》、AcWing题库

1049. 大盗阿福

题目描述

阿福是一名经验丰富的大盗。趁着月黑风高，阿福打算今晚洗劫一条街上的店铺。

这条街上一共有 NN 家店铺，每家店中都有一些现金。

阿福事先调查得知，只有当他同时洗劫了两家相邻的店铺时，街上的报警系统才会启动，然后警察就会蜂拥而至。

作为一向谨慎作案的大盗，阿福不愿意冒着被警察追捕的风险行窃。

他想知道，在不惊动警察的情况下，他今晚最多可以得到多少现金？

输入格式

输入的第一行是一个整数 TT，表示一共有 TT 组数据。

接下来的每组数据，第一行是一个整数 NN ，表示一共有 NN 家店铺。

第二行是 NN 个被空格分开的正整数，表示每一家店铺中的现金数量。

每家店铺中的现金数量均不超过1000。

输出格式

对于每组数据，输出一行。

该行包含一个整数，表示阿福在不惊动警察的情况下可以得到的现金数量。

数据范围

1≤T≤501 \le T \le 50,
1≤N≤1051 \le N \le 10^5

输入样例：

1
2
3
4
5
2
3
1 8 2
4
10 7 6 14

输出样例：

1
2
8
24

样例解释

对于第一组样例，阿福选择第2家店铺行窃，获得的现金数量为8。

对于第二组样例，阿福选择第1和4家店铺行窃，获得的现金数量为10+14=24。

算法分析

在DP的阶段表示中，如果前一个阶段的决策会影响到后面的阶段的决策，那么我们就可以用状态机的形式来做，具体做法就是描述清楚当前的每一个决策

理解题意
  1. 限制
    • 条件限制: 不能连续选择物品
  2. 目标
    • Max物品价值

相比于0101背包，限制条件从物品的体积变为一个条件限制: 不能连续选择物品,也就是我们此时需要关注物品 ii 能否被选。原本限制体积的状态在本题中用于表示是否选择。可以用状态机模型清晰的表示不同状态间的关系.

状态机模型

状态机: 用一些确定的状态及状态间的关系描述一个过程.

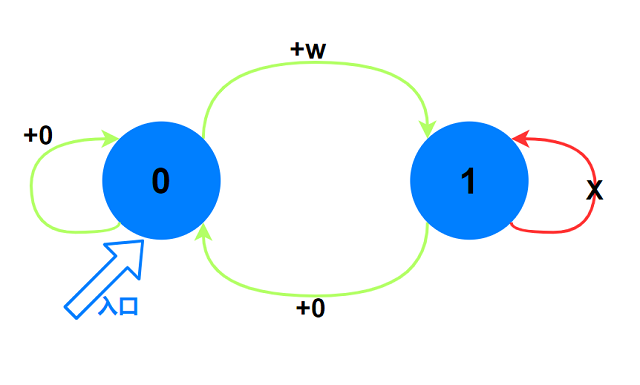
本题中需要表示第ii个物品选/不选两种状态, 且不能连续选择. 状态间的关系如图:

2.png

上图具体含义:

  • 状态: 用0和1分别表示不/选.

  • 有向边: 表示下一个物品选/不选, 每条边表示一次决策; 边权表示这次决策的收益.

  • 阿福的一种选择与图中长度为NN的一条路径一一对应.

依照状态机模型我们就很容易做DPDP分析了.

DPDP分析

状态表示 dp(i,0)dp(i, 0)/dp(i,1)dp(i, 1)

  • 集合: dp(i,j)dp(i, j)表示所有走了ii步且最终状态为jj的路径. j∈[0,1]j\in [0, 1].

  • 属性: Max

状态计算

依据最后一步的选择, 在状态机模型中对应当前状态从何而来:

  • dp(i,0)dp(i, 0): 其上一个状态可以是dp(i−1,0)dp(i - 1, 0)/dp(i−1,1)dp(i - 1, 1), 且对应边的权重均为0 ，有dp(i,0)=max{dp(i−1,0),dp(i−1,1)}dp(i, 0) = max\lbrace dp(i - 1, 0), dp(i - 1, 1)\rbrace.

  • dp(i,1)dp(i, 1): 其上一个状态只能是dp(i−1,0)dp(i - 1, 0). 且对应边的权重为wiw_i, 即物品ii的价值，有p(i,1)=dp(i−1,0)+wip(i, 1) = dp(i - 1, 0) + w_i.

因为阿福的每个决策都与图中长度为NN的路径一一对应, 所以DPDP的计算过程相当于将所有路径的可能都计算了一遍.

Solution

状态机动态规划

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#include <iostream>
using namespace std;
const int N = 1e5 + 10, INF = 0x3f3f3f3f;
int money[N], f[N][2];
int main() {
    int T;
    cin >> T;
    while (T--) {
        int n;
        cin >> n;
        for (int i = 1; i <= n; ++i) cin >> money[i];
        f[0][0] = 0, f[0][1] = -INF;
        for (int i = 1; i <= n; ++i) {
            f[i][0] = max(f[i - 1][0], f[i - 1][1]);
            f[i][1] = f[i - 1][0] + money[i];
        }
        cout << max(f[n][0], f[n][1]) << endl;
    }
}

线性动态规划

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#include <iostream>
using namespace std;
const int N = 1e5 + 10;
int money[N], f[N];
int main() {
    int T;
    cin >> T;
    while (T--) {
        int n;
        cin >> n;
        for (int i = 1; i <= n; ++i) cin >> money[i];
        f[0] = 0, f[1] = money[1];
        for (int i = 2; i <= n; ++i) {
            f[i] = max(f[i - 1], f[i - 2] + money[i]);
        }
        cout << f[n] << endl;
    }
}

1057. 股票买卖

题目描述

给定一个长度为 NN 的数组，数组中的第 ii 个数字表示一个给定股票在第 ii 天的价格。

设计一个算法来计算你所能获取的最大利润，你最多可以完成 kk 笔交易。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。一次买入卖出合为一笔交易。

输入格式

第一行包含整数 NN 和 kk，表示数组的长度以及你可以完成的最大交易数量。

第二行包含 NN 个不超过 1000010000 的正整数，表示完整的数组。

输出格式

输出一个整数，表示最大利润。

数据范围

1≤N≤1051 \le N \le 10^5,
1≤k≤1001 \le k \le 100

输入样例1：

1
2
3 2
2 4 1

输出样例1：

1
2

输入样例2：

1
2
6 2
3 2 6 5 0 3

输出样例2：

1
7

样例解释

样例1：在第 1 天 (股票价格 = 2) 的时候买入，在第 2 天 (股票价格 = 4) 的时候卖出，这笔交易所能获得利润 = 4-2 = 2 。

样例2：在第 2 天 (股票价格 = 2) 的时候买入，在第 3 天 (股票价格 = 6) 的时候卖出, 这笔交易所能获得利润 = 6-2 = 4 。随后，在第 5 天 (股票价格 = 0) 的时候买入，在第 6 天 (股票价格 = 3) 的时候卖出, 这笔交易所能获得利润 = 3-0 = 3 。共计利润 4+3 = 7.

算法分析

cb8092d74acad480814865d74231b98.png

初始化：

  • f[0][j][0/1] = -INF，无效，0个物品却进行了j次交易，不可能
  • f[i][0][1] = -INF，无效，没进行交易却持有物品，不可能
  • f[i][0][0] = 0，有效，没进行交易，也未持有，收益0

先将f全部设置为无效状态-INF，再单独处理有效的起始状态f[i][0][0] = 0

入口为f[0][0][0]

注意：

  • 这里状态机的过程，对于每个股票，要么就买，要么就卖，不能说是买了然后在同一个点直接卖掉，这样是不符合状态机模型的，因此对于上述转移方程可以会有人提出疑问。

  • 为什么状态转移方程不能是下面代码，即卖的时候才算做了一次交易，原代码是买的时候才算一次交易

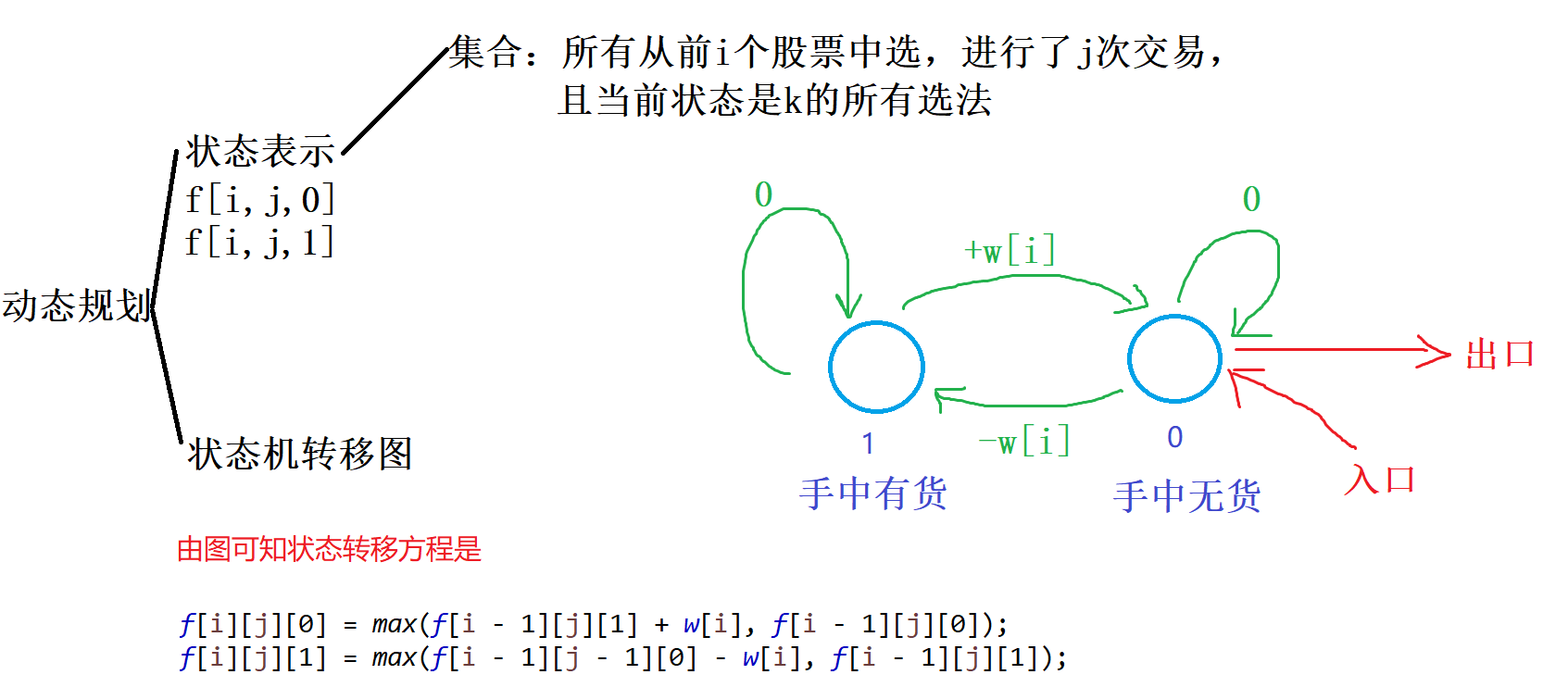
1
2
f[i][j][0] = max(f[i - 1][j - 1][1] + w[i], f[i - 1][j][0]);
f[i][j][1] = max(f[i - 1][j][0] - w[i], f[i - 1][j][1]);

终究要回归到状态转移的起点，第一支股票只有买，和不买这两个操作，一定不可能是卖和不卖的这两个操作，因此第一支股票如果买入时，必须按照一次交易处理。否则如果第一次股票如果买入时，不按一次交易处理，也就代表着第一支股票卖出才算一次交易，也就代表着在第一支股票卖出之前还买了一支股票，显然是矛盾的。

时间复杂度 O(nm)O(nm)

空间复杂度 O(m)O(m)

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include <iostream>
#include <cstring>
using namespace std;
const int N = 1e5 + 10, M = 110;
int f[N][M][2];
int money[N];
int main() {
    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; ++i) cin >> money[i];
    
    //f[0][j][0/1] = 无效，0个物品却进行了j次交易，不可能
    //f[i][0][1] = 无效，没进行交易却持有物品，不可能
    //f[i][0][0] = 0，没进行交易，也未持有，有效状态，收益0
    memset(f, 0xc0, sizeof f);
    for (int i = 0; i <= n; ++i) f[i][0][0] = 0;
    
    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= m; ++j) {//j = 0已在初始化时计算，f[i][0][1] = 无效，f[i][0][0] = 0
            f[i][j][0] = max(f[i - 1][j][0], f[i - 1][j][1] + money[i]);
            f[i][j][1] = max(f[i - 1][j - 1][0] - money[i], f[i - 1][j][1]);
        }
    }
    
    int ans = 0;
    for (int j = 0; j <= m; ++j) ans = max(ans, f[n][j][0]);
    cout << ans;
}

滚动数组优化空间

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#include <iostream>
#include <cstring>
using namespace std;
const int N = 1e5 + 10, M = 110;
int f[2][M][2];
int money[N];
int main() {
    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; ++i) cin >> money[i];
    
    memset(f, 0xc0, sizeof f);
    f[0][0][0] = f[1][0][0] = 0;
    
    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= m; ++j) {
            f[i & 1][j][0] = max(f[(i - 1) & 1][j][0], f[(i - 1) & 1][j][1] + money[i]);
            f[i & 1][j][1] = max(f[(i - 1) & 1][j - 1][0] - money[i], f[(i - 1) & 1][j][1]);
        }
    }
    
    int ans = 0;
    for (int j = 0; j <= m; ++j) ans = max(ans, f[0][j][0]);
    for (int j = 0; j <= m; ++j) ans = max(ans, f[1][j][0]);
    cout << ans;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include <iostream>
#include <cstring>
using namespace std;
const int N = 1e5 + 10, M = 110;
int f[M][2];
int money[N];
int main() {
    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; ++i) cin >> money[i];
    
    memset(f, 0xc0, sizeof f);
    f[0][0] = 0;
    
    for (int i = 1; i <= n; ++i) {
        for (int j = m; j >= 1; --j) {
            f[j][0] = max(f[j][0], f[j][1] + money[i]);
            f[j][1] = max(f[j - 1][0] - money[i], f[j][1]);
        }
    }
    
    int ans = 0;
    for (int j = 0; j <= m; ++j) ans = max(ans, f[j][0]);
    cout << ans;
}

1058. 股票买卖 V

题目描述

给定一个长度为 NN 的数组，数组中的第 ii 个数字表示一个给定股票在第 ii 天的价格。

设计一个算法计算出最大利润。在满足以下约束条件下，你可以尽可能地完成更多的交易（多次买卖一支股票）:

  • 你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。
  • 卖出股票后，你无法在第二天买入股票 (即冷冻期为 11 天)。

输入格式

第一行包含整数 NN，表示数组长度。

第二行包含 NN 个不超过 1000010000 的正整数，表示完整的数组。

输出格式

输出一个整数，表示最大利润。

数据范围

1≤N≤1051 \le N \le 10^5

输入样例：

1
2
5
1 2 3 0 2

输出样例：

1
3

样例解释

对应的交易状态为: [买入, 卖出, 冷冻期, 买入, 卖出]，第一笔交易可得利润 2-1 = 1，第二笔交易可得利润 2-0 = 2，共得利润 1+2 = 3。

算法分析

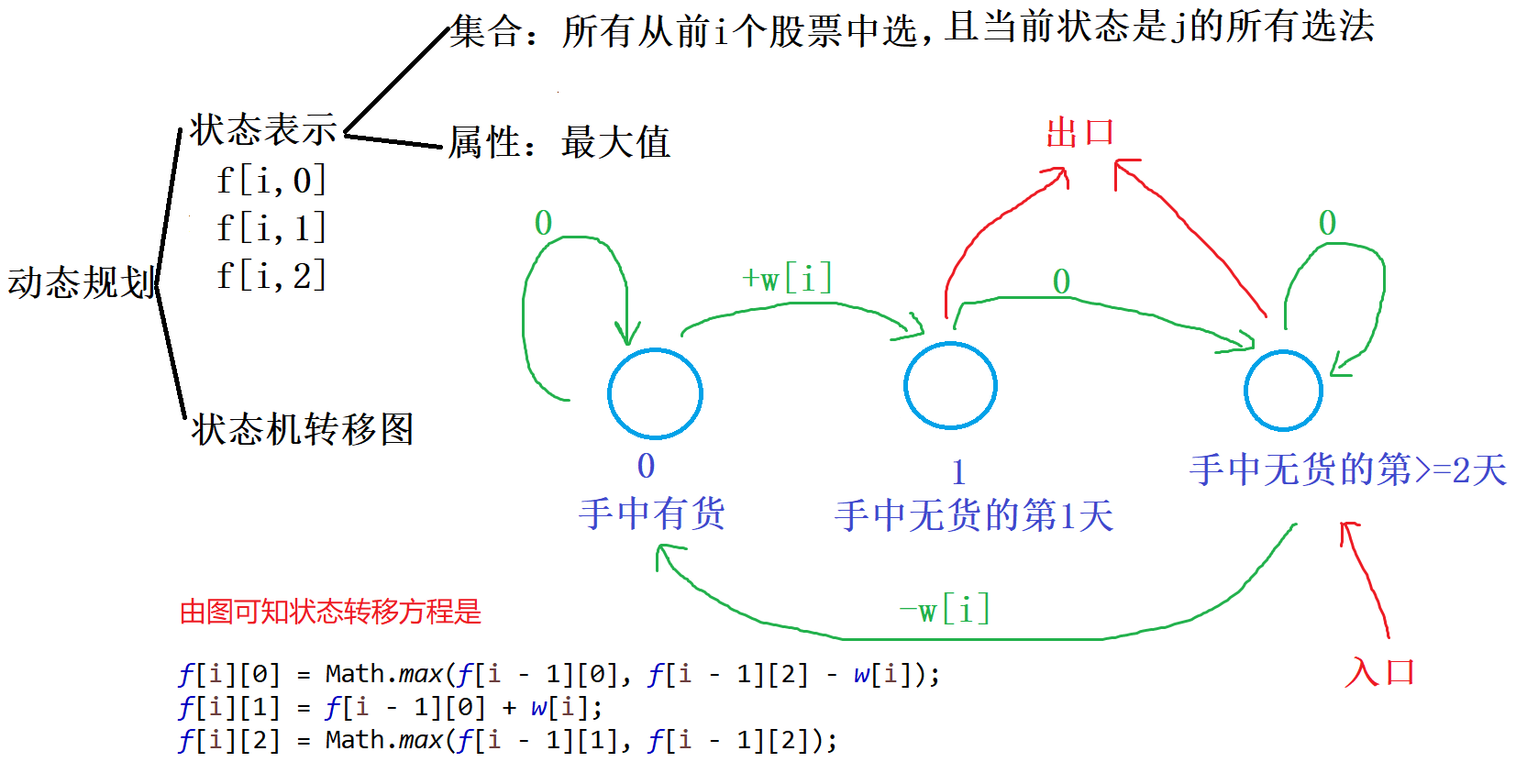
6bc433e74040b6b70db97b7da6b89e4.png

初始化：f[0][2] = 0，f[0][0] = f[0][1] = -INF， 因为在第0个股票一定是无货的，且可以买入，必定从2这个状态开始转移才有效

出口：可能最后一天才卖出，也可能最后一天是最后一次卖出操作好几天后了，故取max(f[n][1],f[n][2])

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#include <iostream>
#include <cstring>
using namespace std;
const int N = 1e5 + 10;
int money[N], f[N][3];
int main() {
    int n; 
    cin >> n;
    for (int i = 1; i <= n; ++i) cin >> money[i];
    
    memset(f, 0xc0, sizeof f);
    f[0][2] = 0;
    
    for (int i = 1; i <= n; ++i) {
        f[i][0] = max(f[i - 1][0], f[i - 1][2] - money[i]);
        f[i][1] = f[i - 1][0] + money[i];
        f[i][2] = max(f[i - 1][1], f[i - 1][2]);
    }
    
    cout << max(f[n][1], f[n][2]);
}

滚动数组优化空间

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#include <iostream>
#include <cstring>
using namespace std;
const int N = 1e5 + 10;
int money[N], f[2][3];
int main() {
    int n; 
    cin >> n;
    for (int i = 1; i <= n; ++i) cin >> money[i];
    
    memset(f, 0xc0, sizeof f);
    f[0][2] = 0;
    
    for (int i = 1; i <= n; ++i) {
        f[i & 1][0] = max(f[(i - 1) & 1][0], f[(i - 1) & 1][2] - money[i]);
        f[i & 1][1] = f[(i - 1) & 1][0] + money[i];
        f[i & 1][2] = max(f[(i - 1) & 1][1], f[(i - 1) & 1][2]);
    }
    
    cout << max(f[n & 1][1], f[n & 1][2]);//注意这里的 n & 1
}

1052. 设计密码（字符串匹配自动机 + KMP）

题目描述

你现在需要设计一个密码 SS，SS 需要满足：

  • SS 的长度是 NN；
  • SS 只包含小写英文字母；
  • SS 不包含子串 TT；

例如：abcabc 和 abcdeabcde 是 abcdeabcde 的子串，abdabd 不是 abcdeabcde 的子串。

请问共有多少种不同的密码满足要求？

由于答案会非常大，请输出答案模 109+710^9+7 的余数。

输入格式

第一行输入整数N，表示密码的长度。

第二行输入字符串T，T中只包含小写字母。

输出格式

输出一个正整数，表示总方案数模 109+710^9+7 后的结果。

数据范围

1≤N≤501 \le N \le 50,
1≤∣T∣≤N1 \le |T| \le N，∣T∣|T|是TT的长度。

输入样例1：

1
2
2
a

输出样例1：

1
625

输入样例2：

1
2
4
cbc

输出样例2：

1
456924

算法分析

字符串匹配自动机 + KMP详细解释见 一文吃透字符串匹配！

f[i][j]：生成了i个密码，且状态停留在j，即有限自动机读入了i个字符，且ϕ(Ti)=j\phi(T_i)=j

状态j也表示已成功匹配j个字符

算法流程：

  • 循环生成密码字符个数，正在生成第i个字符
  • 枚举生成i - 1个密码字符后，所停留的状态 ϕ(Ti−1)=j\phi(T_{i-1})=j
  • 枚举正在生成的是什么字符，T[i]=a∼zT[i] = a \sim z
  • 计算状态转移，求 ϕ(Ti)=δ(j,T[i])\phi(T_i) = \delta(j,T[i]) ，转移函数用KMP算法的前缀函数 π()\pi() 来实现
  • 状态转移从j到q，更新计算f[i][q]的方案数
  • 计算最终所有方案数，生成完n个密码字符，且状态不停留在m的方案都满足条件，累加起来

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include <iostream>
using namespace std;
const int N = 60, mod = 1e9 + 7;
int f[N][N], ne[N];
int main() {
  int n;
  cin >> n;
  string p;
  cin >> p;
  int m = p.size();
  p = " " + p;
  
  for (int i = 2, j = 0; i <= m; ++i) {
    while (j > 0 && p[i] != p[j + 1]) j = ne[j];
    if (p[i] == p[j + 1]) ++j;
    ne[i] = j;
  }
  
  f[0][0] = 1;
  for (int i = 1; i <= n; ++i) {
    for (int j = 0; j < m; ++j) {//枚举处理前i - 1个字符后停留的状态
      for (char c = 'a'; c <= 'z'; ++c) {
        int q = j;
        while (q > 0 && c != p[q + 1]) q = ne[q];
        if (c == p[q + 1]) ++q;
        if (q < m) f[i][q] = (f[i][q] + f[i - 1][j]) % mod;
      }
    }
  }
  
  int ans = 0;
  for (int j = 0; j < m; ++j) ans = (ans + f[n][j]) % mod;
  cout << ans;
}

1053. 修复DNA

题目描述

生物学家终于发明了修复DNA的技术，能够将包含各种遗传疾病的DNA片段进行修复。

为了简单起见，DNA看作是一个由’A’, ‘G’ , ‘C’ , ‘T’构成的字符串。

修复技术就是通过改变字符串中的一些字符，从而消除字符串中包含的致病片段。

例如，我们可以通过改变两个字符，将DNA片段”AAGCAG”变为”AGGCAC”，从而使得DNA片段中不再包含致病片段”AAG”，”AGC”，”CAG”，以达到修复该DNA片段的目的。

需注意，被修复的DNA片段中，仍然只能包含字符’A’, ‘G’ , ‘C’ , ‘T’。

请你帮助生物学家修复给定的DNA片段，并且修复过程中改变的字符数量要尽可能的少。

输入格式

输入包含多组测试数据。

每组数据第一行包含整数N，表示致病DNA片段的数量。

接下来N行，每行包含一个长度不超过20的非空字符串，字符串中仅包含字符’A’, ‘G’ , ‘C’ , ‘T’，用以表示致病DNA片段。

再一行，包含一个长度不超过1000的非空字符串，字符串中仅包含字符’A’, ‘G’ , ‘C’ , ‘T’，用以表示待修复DNA片段。

最后一组测试数据后面跟一行，包含一个0，表示输入结束。

输出格式

每组数据输出一个结果，每个结果占一行。

输入形如”Case x: y”，其中x为测试数据编号（从1开始），y为修复过程中所需改变的字符数量的最小值，如果无法修复给定DNA片段，则y为”-1”。

数据范围

1≤N≤501 \le N \le 50

输入样例：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
2
AAA
AAG
AAAG    
2
A
TG
TGAATG
4
A
G
C
T
AGT
0

输出样例：

1
2
3
Case 1: 1
Case 2: 4
Case 3: -1

算法分析

Solution